高中概率题中数学思想方法的运用探微

江苏省海门中学 邓 杰

数学思想作为对数学规律的运用与总结，是解决问题的基本思路之一。常见的数学思想方法有推断、分类讨论、数形结合、模型化、公理化和随机化等，属于数学科目的精髓和灵魂。在高中数学知识学习过程中，概率题是一种较为特殊的题目，题型也显得与众不同，教师需指导学生学会运用数学思想方法来分析和解答概率题，从而提高解题的准确度与速度。

一、运用列举事件思想方法，清晰求解题目答案

高中数学中的概率题虽然难度一般，但是对学生的逻辑思维能力和分析能力要求较高，在一般题型中经常要用到列举事件的方式来求解，现已得到广泛的使用，这其实就是对列举事件数学思想方法的运用。因此，在解决高中数学概率题时，教师要提倡学生运用列举事件的数学思想方法，使其结合题意，把可能发生的所有事件都罗列出来并进行逐个分析，随后挑选出满足题目要求的事件，这样他们能够清晰、准确地挑选出正确答案，降低错误现象的出现。

例如：假如一次同时抛掷三枚硬币，那么正好有两枚反面朝下、一枚正面朝上的概率是多少？解析：在抛掷硬币时，每枚硬币的结果只有反面与正面两种情况，三枚硬币同时抛掷会出现以下8种情况：反反反、反反正、反正反、反正正、正反正、正反反、正正反、正正正。其中满足题目要求的有反反正、反正反和正反反3种，那么要求解的概率是38。又如：在某次数学考试中，甲、乙、丙三人及格(互不影响)的概率0.4、0.2、0.5，考试结束后，最容易出现几个人及格？解答：按以下四种情况计算概率，三人都及格的概率P1；三个人都不及格的概率P2；恰有两人及格的概率P3；恰有1人及格的概率P4，通过计算，最容易出现的是恰有1人及格的情况。

如此，运用列举事件的数学思想方法，把可能出现的所有情况均罗列出来，帮助学生清晰地认识题目，把复杂的概率问题变得简单化，通过认真分析和筛选，找出符合题目要求的情况。由浅入深、由此及彼，在教师的引领与启发下，让学生乐在其中、学在其中，渐进式地感悟数学思想的魅力所在，促进学生在数学学习上的可持续发展。

二、应用数形结合思想方法，简化学生解题过程

数形结合是一个惯用的数学思想方法，贯穿于整个教育阶段，包括小学、初中和高中等，适用的题目类型也较为广泛。在处理高中数学概率题时，部分题目如果直接采用公式法将会显得异常复杂、困难，要想顺利解决，针对条件组合类的概率题，可以应用数形结合的思想方法。为此，教师应结合具体题目，指导学生应用数形结合的思想方法来解答概率题，通过图像把抽象化的概率题变得直观化、具体化，优化他们的解题思路，简化解题过程。

例如：甲、乙两人计划上午8点至9点之间在体育场见面，规定无论谁先到体育场均等待15分钟，假如对方仍然没有到达就可以离开，那么甲、乙两人可以见面的概率是多少？解析：由于甲、乙两人计划的时间为8点至9点，共1个小时，该时间段一共是60分钟，可以建立一个平面直角坐标系，分别用x轴与y轴代表甲、乙两人达到体育场的时间，并设甲、乙两人达到体育场的时间分别是x与y，由于先到15分钟的可以离开，那么两人可以见面的条件为丨x-y丨≤15，如下图所示：

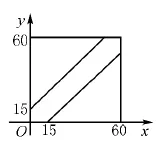
其中正方形表示整个时间，上下两个三角形表示甲、乙无法见面的时间，剩余的中间部分则表示甲、乙两人可以见面的时间，计算出该部分所占正方形面积的比例，即求出两人见面的概率。

上述案例中的概率题很难采用学习过的理论和公式求解，把题目中的已知条件在图像中呈现出来，通过数形结合，学生可以简洁、直观地分析，将问题变得直白和简单，还容易理解。

三、采用对立求解思想方法，快速解决概率问题

对立事件指的是：A和B的交集是不可能事件，A和B的并集则是必然事件，那么A事件和B事件就相互对立，是一组对立事件，即A事件和B事件必须且仅有一个发生，这同样是一种典型的数学思想方法。在解答高中数学概率题时，遇到包含情况较多的求解类事件时，教师可以引导学生采用对立求解的数学思想方法。由于所有事件的总概率是1，那么用1减去对立事件的发生概率，就能够求出题目中所要求的概率，从而快速解决问题。

例如：将一个骰子先后投掷两次，那么出现点数之和小于12的概率是多少？解析：由于题目中是将骰子先后投掷两次，表明每次投掷的结果不会受到外界因素的影响，而且每次投掷结果是1至6点的概率相同，都是1/6。求的是两次投掷结果点数之和小于12的事件，可以把该事件设为A，那么两次投掷结果点数之和大于等于12的事件就是A事件的对立事件，用B来表示，且B事件发生的概率为1减去A事件发生的概率。因为两次投掷结果点数之和小于12出现的情况比较多，点数之和大于等于12的情况仅有一种，即为6、6。两次投掷骰子出现点数一共有6×6＝36种情况，则P（B）＝，得出P（A）＝1-＝，也就是说出现点数之和小于12的概率是。

针对上述案例，当所求概率对立事件出现情况较少或容易表示时，可以使用对立求解的数学思想方法，先求出对立事件发生的概率，再求出正确答案，以此减少错误情况的出现。此时，数学思想方法不仅让学生轻松解决了相应的问题，更让学生增长了智慧与技能，促进学生综合素养的提升。

高中数学中涉及的思想方法有很多，适用于概率题的也不少，教师在日常教学中，需刻意渗透各种数学思想方法，学生在解题中要善于总结和积累，根据具体题目选用相应的数学思想方法，不断提升解题的针对性和效率。