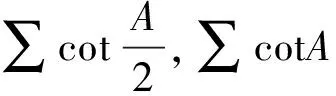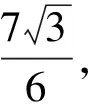欧拉不等式一个三角形式的类比

杨续亮 苏岳祥

(安徽省岳西县汤池中学 246620)

1 引言

设△ABC的三边为a,b,c，外接圆和内切圆半径分别为R,r，则有著名的欧拉不等式R≥2r，

文[1]建立了欧拉不等式的一个三角形式：

定理1设R,r分别为△ABC外接圆和内切圆半径，则有(∑表示循环和)

当且仅当△ABC为正三角形时取等号.

文[2]给出了欧拉不等式的一个三角形式的类似：

定理2设R,r分别为△ABC外接圆和内切圆半径，则有(∑表示循环和)

当且仅当△ABC为正三角形时取等号.

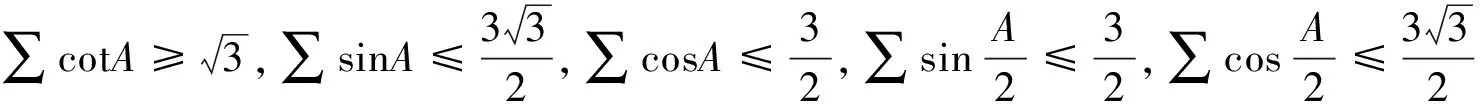
2 构建新的欧拉三角不等式

定理3设R,r分别为△ABC外接圆和内切圆半径，则有(∑表示循环和)

当且仅当△ABC为正三角形时取等号.

定理4设R,r分别为△ABC外接圆和内切圆半径，则有(∑表示循环和)

当且仅当△ABC为正三角形时取等号.

定理5设R,r分别为△ABC外接圆和内切圆半径，则有(∑表示循环和)

当且仅当△ABC为正三角形时取等号.

定理6设R,r分别为△ABC外接圆和内切圆半径，则有(∑表示循环和)

当且仅当△ABC为正三角形时取等号.

定理7设R,r分别为△ABC外接圆和内切圆半径，则有(∑表示循环和)

当且仅当△ABC为正三角形时取等号.

3 预备知识

为了证明上述定理3-7，先给出△ABC中的预备等式和不等式：

设△ABC的三边为a,b,c，外接圆半径、内切圆半径和半周长分别为R,r,s，则有

16Rr-5r2≤s2≤4R2+4Rr+3r2(Gerrestsen不等式)，

4 定理的证明

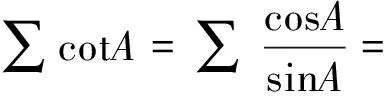
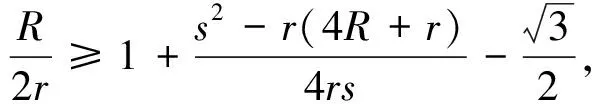
由16Rr-5r2≤s2≤4R2+4Rr+3r2，

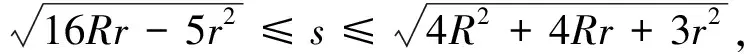
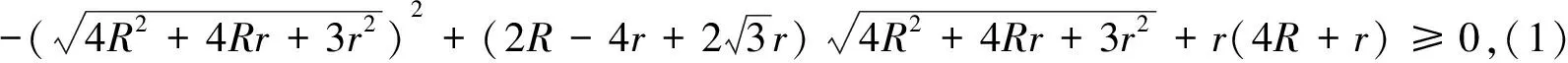
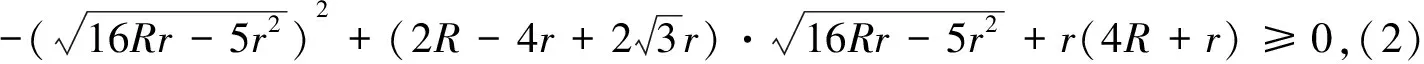
(1)式等价于

(2)式等价于

由欧拉不等式R≥2r易知以上两式均成立，从而定理3得证.

定理4的证明运用定理2来证明，

而由16Rr-5r2≤s2≤4R2+4Rr+3r2，

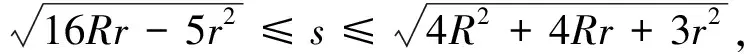
故

而

由欧拉不等式R≥2r可得

从而定理4得证，

评注从本证明过程可以看出，定理2强于定理4.

定理5的证明

而由16Rr-5r2≤s2≤4R2+4Rr+3r2，

由欧拉不等式R≥2r可得

从而定理5得证.

定理6的证明

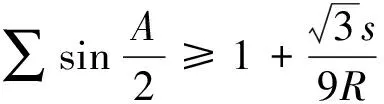
定理7的证明

由不等式

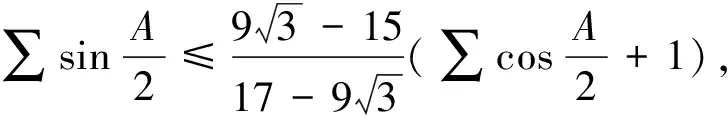
从而得到

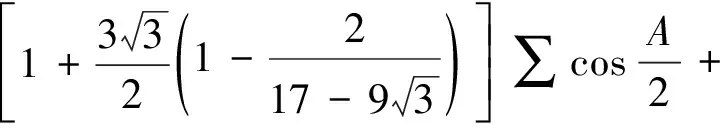
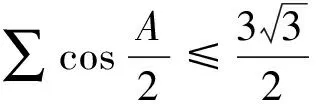
从而定理7获证.

我们可以从以上定理2和4，5，6，7的证明可以得出一个欧拉不等式三角形式的不等式链.

定理8设R,r分别为△ABC外接圆和内切圆半径，则有(∑表示循环和)

当且仅当△ABC为正三角形时取等号.