指向核心素养的两角差的余弦公式教学再设计

高长玉

(安徽省淮南市第二中学 232001)

“两角差的余弦公式”(简称差余公式)是经典内容，涉及的数学知识广泛，包含了丰富的数学思想与方法.本课的教学对学生获得“四基”、提升“四能”、培养数学思维和发展数学学科核心素养都很有作用.本文在分析这一内容教学现状的基础上，以发展学生数学学科核心素养为指向，给出笔者的教学设计，敬请同行批评指正.

1 教学现状分析

1.1 教材现状

对比几种不同版本教材，发现对本节知识引入与展开的处理方式有所不同：

(1)人教A版：先在章头图创设了一个涉及两角和三角函数的实际应用问题情境，再在单位圆中推导α,β为锐角，且α>β时的两角差余弦公式cos(α-β)，最后再借助向量工具证明α,β取任意角的一般情况.

(2)人教B版：直接提出“如何计算α+β，α-β的三角函数”，随即给出公式.

与北师大版教材处理方式类似，苏教版和湘教版教材也采用向量数量积引导出差余公式.

1.2 课堂教学现状

受教材编写意图引导、教师理念和学生能力差异等因素的影响，目前对本节知识引入与展开常见以下几种方式.

(1)问题铺垫、单刀直入式

按人教B版的方式，教师先是抛出诸如“如何求值sin75°,cos15°”的问题引出课题“两角和与差的余弦公式”，再用向量法推导差余公式.

(2)情境设置、“猜想”指引式

教师设置类似于人教A版章头图中实际应用的问题情境，引入研究课题，继而呈现诸如：

cos30°=cos(60°-30°)

cos90°=cos(120°-30°)

=cos120°cos30°+sin120°sin30°=0，

的结论，让学生直观感知，猜想公式，再引导学生用向量法给予证明.

(3)“巧设”问题、引导“探究”式

教师设置诸如“已知a=(cos75°,sin75°),b=(cos45°,sin45°),试求a·b的值”的问题，然后给出计算a·b的两种方法：

解法一：a·b=cos75°cos45°+sin75°·sin45°；

解法二：a·b=a·bcos30°=cos30°，

再猜想公式，并用向量法证明.

对于上述知识引入、展开的方式，笔者认为有以下几个值得商榷的问题：

第一，设置的问题有些突兀，不自然，不连贯，教师的主观意志强；

第二，缺乏必要的引导，公式的发现成为“被发现”，导致学生思维的参与度不高.

第三，没有顾及学生的认知准备现状，在理解数学、理解学生、理解教学上都存在欠缺.

2 教学再设计

针对上述问题，并考虑到笔者所在学校是省级示范高中，生源状况较好的实际，笔者对本课的教学进行了再设计，通过教学实践检验，收到较好效果.下面呈现几个片断.

片断一设置问题情境、引入新课

问题(1) 前面我们曾学习过许多三角函数诱导公式，你能写出一些与大家分享吗？

问题(2) 通过这些诱导公式你能提出一些新问题吗？你有哪些初步的判断？

对于问题(1)，要求学生写的越多越好；通过问题(1)的分享，为问题(2)的思考做好铺垫.

通过对三角函数诱导公式的举例，引导学生对诱导公式进行观察、比较、分析，初步判断两角和与差的正余弦函数sin(α±β),cos(α±β)与两个角的正弦sinα,sinβ和余弦cosα,cosβ都有关系.

设计意图①通过对诱导公式共性的归纳，给两角和与差的三角函数公式提供猜想的指向，即两角和与差的正、余弦与两角的正、余弦皆有关系(但不是简单的“分配律”的关系)；

②从诱导公式出发，在学生思维的“最近发展区”内提出问题，启发学生从特殊到一般，思考两角和与差的三角函数问题，有利于学生展开创造性思维，得出有关猜想.

片断二猜想公式、知识展开

(1)研究对象的选择

探究1： 两角和的问题可以转化为两角的差吗？反之呢？

探究2： 当α,β都是锐角且α>β时，α+β一定为锐角吗？α-β呢？

学生在完成这两个探究之后，自然选择了先研究差角的余弦.

设计意图①让学生体验化归与转化的数学思想方法，使其有一种金蝉脱壳的惬意；

②渗透从“特殊”入手的研究策略，帮助学生找到思维的切入点.

(2)探究特殊结论

学生联想到同样是“特殊情况”的三角函数诱导公式的推导方法，自然会想到：可以考虑在直角坐标系中，借助于单位圆，利用三角函数线探究锐角α-β的余弦函数.

笔者用问题串的形式引导学生作如下思考：

问题1：如图1，在单位圆中，为了便于作出角α-β的余弦线，你认为设哪两个角为α、β较为妥当？

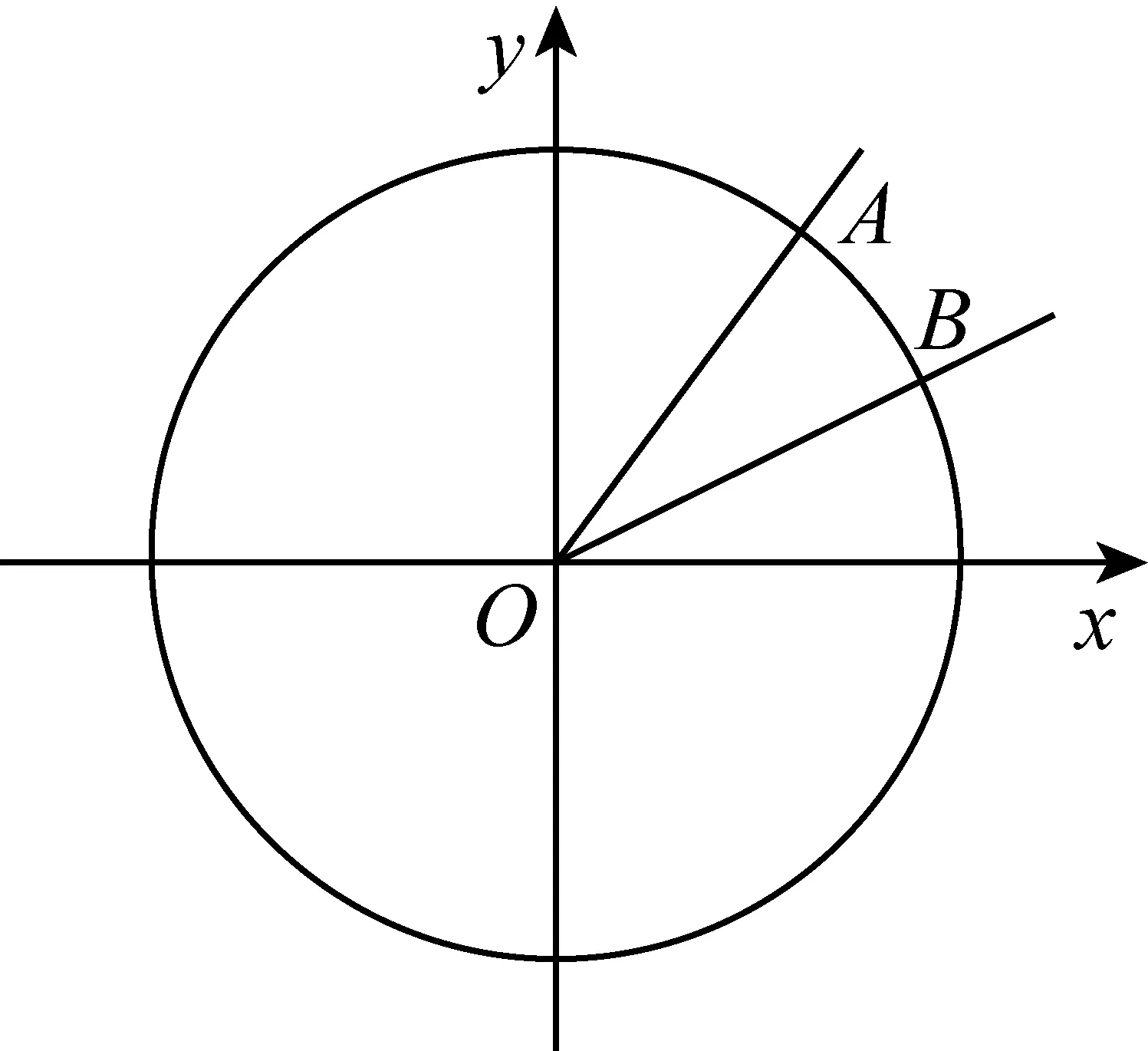
图1

图2

设∠AOx=α，∠AOB=β，如图2，过点B作BC⊥x轴(点C为垂足)，则cos(α-β)=OC.

由初步判断，α-β的余弦与sinα,sinβ和cosα,cosβ都有关系.但对于角β，它的两边均不与x轴非负半轴重合，引导学生考虑构造含角β的直角三角形.

问题2： 怎样构造含角β的直角三角形？你是如何想到的？

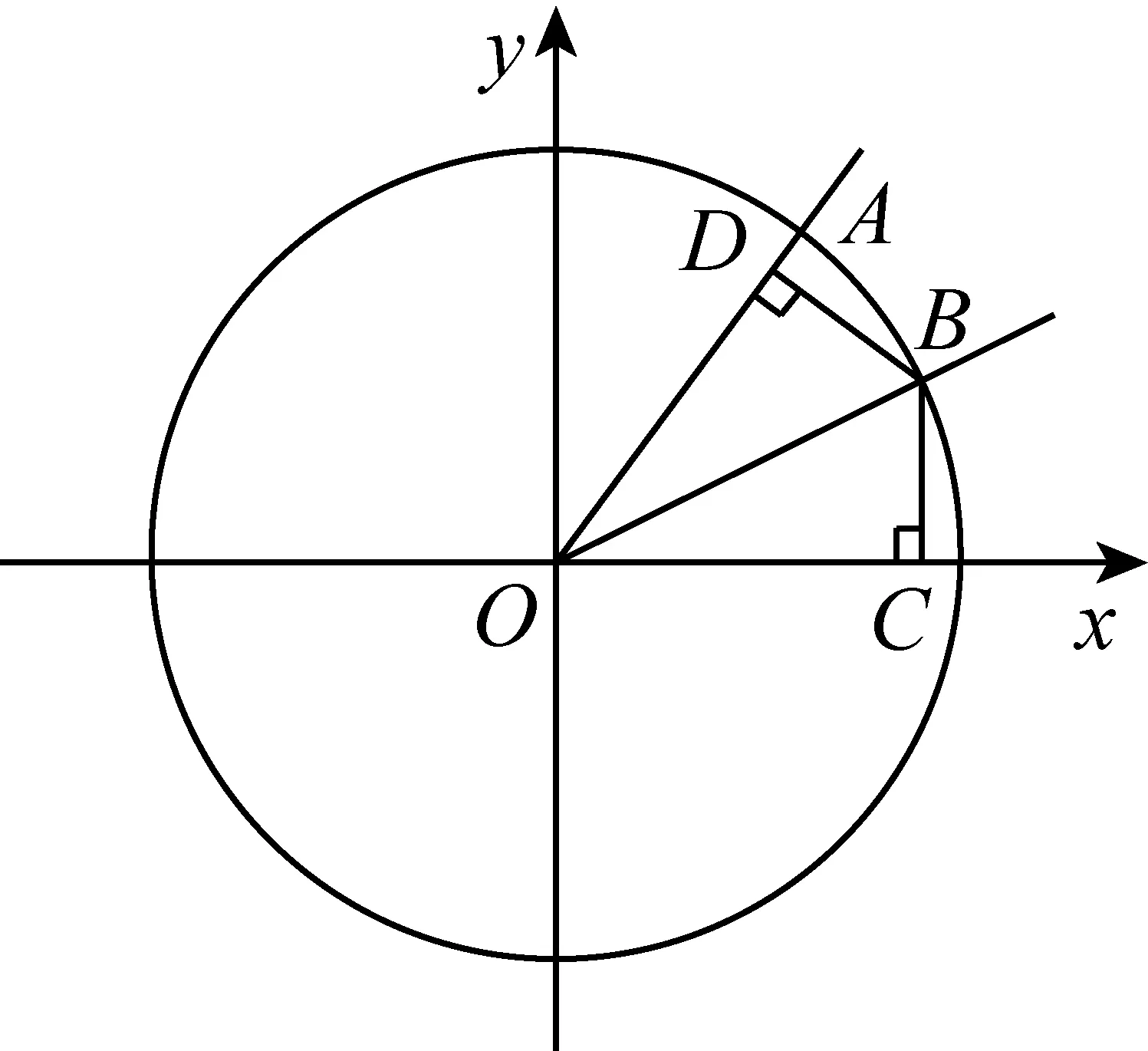
图3

如图3，学生一般会选择过点B作BD⊥OA(点D为垂足),理由是“BD与BC方便建立联系”.

问题3： 如图3，在Rt△BOD中，已知什么，可知什么？

学生容易回答，已知∠AOB=β，OB=1,可知OD=cosβ，DB=sinβ.

问题4： 如何建立未知线段OC与已知线段OD、DB的联系？

利用几何画板，分别用黄色、红色闪现已知、未知线段，结合笔者在解题教学中经常提到的“四个什么”——已知什么，可知什么，要知什么，想知什么.学生会想到把这两条已知线段投影到x轴上，可使未知与已知联系起来.

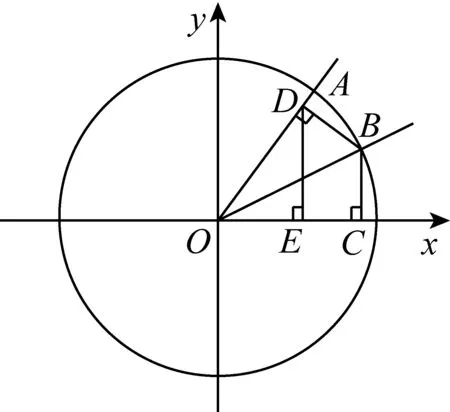
图4

如图4，过点D作DE⊥OC(点E为垂足),则OC=OE+EC.

启发学生，要求OE，就要观察OE所在的三角形，学生容易得出OE=OD·cos∠BOD=cosβ·cosα.

如何求EC的长自然地成了一个呼之欲出的问题.

问题5： 在直角梯形ECBD中(如图4)，可以知道哪些已知条件？

除了直角外，考虑到发现∠EDB=∠AOx=α有一定难度，可以借助多媒体将∠EDB与∠AOx的两边分别用绿色与紫色间隔性闪烁.

问题6： 在直角梯形中，求边长问题，我们常用的方法是什么？

学生一般有两种转化方法：一种是过点B作BF⊥DE(点F为垂足)(如图5);另一种方法是过点C作CF∥BD交DE于点F.都可以得出EC=sinβ·sinα(如图6).

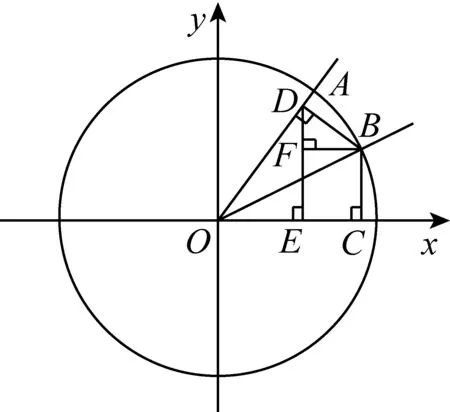
图5

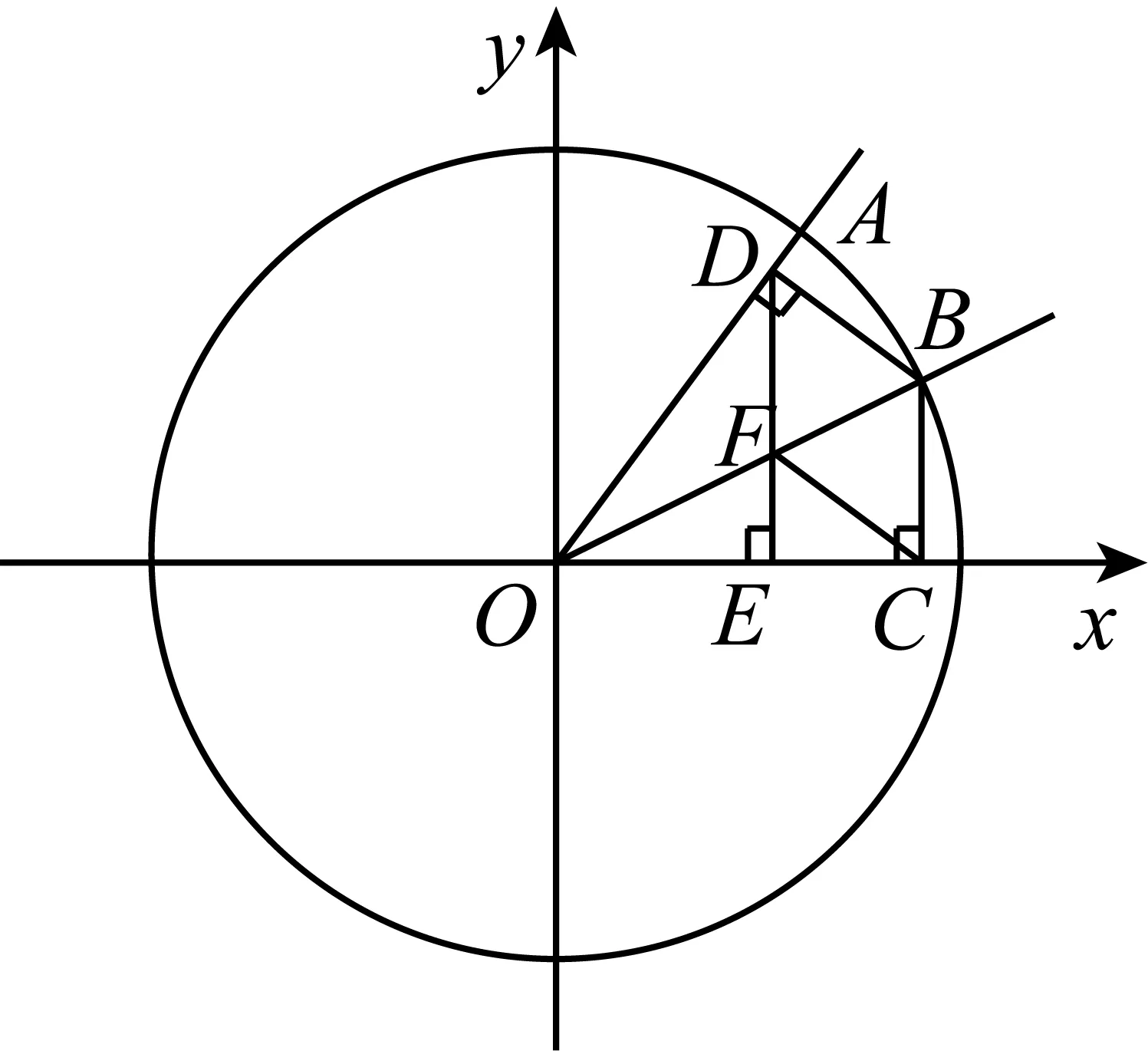
图6

因此，有结论cos(α-β)=cosαcosβ+sinαsinβ.

设计意图在学生的思维最近发展区内提问，通过层层递进的问题引导学生思考与探究，给学生留下充分的悟的时间，使公式的发现一步步拾阶而上.

问题7： 基于研究问题所采用的“从特殊到一般”的归纳策略，你会提出怎样的猜想？

学生容易得出猜想：对任意角α,β,cos(α-β)=cosαcosβ+sinαsinβ成立.

追问：观察表达式的右边，从运算上看是什么形式？这与前面我们学过的哪一种运算在形式上类似？

学生容易想到平面向量的数量积运算.由于表达式右边的结构是x1x2+y1y2的形式，学生想到构造向量(x1,y1)与(x2,y2)已是情理之中.

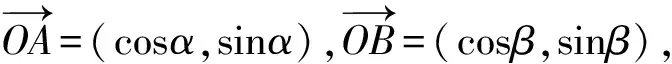
接着利用向量的数量积定义知猜想“正确”.

问题8： 你认为以上推导天衣无缝吗？

在学生满足于成功的喜悦之际，突然这么一问，很有戏剧性，容易引起学生的好奇心和求知欲.

在学生百思不得其解的情况下，教师适时点拨，请他们回忆一下向量夹角的范围.他们很快会意识到以上只是证明了“α,β∈[0,π]，且α>β时，猜想成立”.

设计意图渗透由特殊到一般的归纳策略，通过观察、归纳、猜想培养学生的创造性思维能力；问题8的设计对培养学生的批判思维能力，对规范答题，解决“会而不对”、“对而不全”等问题很有帮助.

问题9： 针对以上角α与β的大小关系，你会作怎样的分类？

当α=β时，结论显然成立；

当α<β时，可以从两个角度说明猜想成立：一是由诱导公式cos(α-β)=cos(β-α)，二是从余弦函数的奇偶性.

问题10： 现在已经证明了“α,β∈[0,π]时猜想成立”，怎样扩大α,β的范围？

学生意识到只要证明一个周期内猜想成立，再根据周期性便知任意角时猜想也成立，学生通过自主探究，可以有以下两种处理方法：

方法一：设α∈(π,2π]，β∈[0,π]，令α=π+θ，

则左边=cos(π+θ-β)=-cos(θ-β)，

而右边=cos(π+θ)cosβ+sin(π+θ)sinβ

=-(cosθcosβ+sinθsinβ)，

又cos(θ-β)=cosθcosβ+sinθsinβ，从而结论成立.

考虑到对称性，β∈(π,2π]时结论也成立.至此，证明了“α,β∈[0,2π]时，cos(α-β)=cosαcosβ+sinαsinβ”成立.

方法二：因为α,β∈[0,π]时猜想成立，

所以α,β∈[-π,0]时猜想成立(因为余弦函数为偶函数).

所以α,β∈[-π,π]时猜想成立.

设计意图“从揭露已有知识在解决新问题时遇到的困难开始，以引起学生的好奇心和求知欲，调动学生探究新知的积极性”[1]在这一思想的指导下，培养学生分类讨论、化归与转化的数学思想方法，让学生进一步感悟由特殊到一般的归纳策略.

3 结束语

章建跃博士认为，“四个理解(理解数学、理解学生、理解技术、理解教学)”是教师专业化发展的必由之路，也是提高教学质量的根本保证.他同时强调，课堂教学要发挥数学的内在力量，在整个教学内容的展开过程中，都要发挥“一般观念”的作用，加强“如何思考”、“如何发现”的启发和引导.

在此思想的指导下，这节课本着一切数学课堂教学活动都从数学的本质出发，重视数学探究，关注学生发展.教学情境的设置既遵循数学知识的内在逻辑关系，又符合学生发展的需要，并辅之以信息技术手段，使得课堂教学科学而自然，“拉近”了教师、教材与学生之间的距离，学生身临其境地经历了数学知识的发生、发展的过程，切实地感悟到数学地认识问题、分析问题、解决问题的思想方法，对发展学生的“四基”、“四能”，理解数学知识的发生发展过程，进而提升数学素养等都具有非常积极的意义[2].