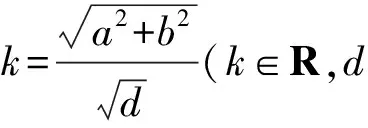关于格点三角形相似问题的研究

胡 涛

(安徽省教育科学研究院 230061)

问题已知△A1B1C1是n×n的方格纸中的一个格点三角形,画出一个格点△A2B2C2,使△A2B2C2∽△A1B1C1.

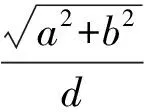
证明如图1， 设A1(m1，n1),B1(0，0),C1(p1，q1),A2(m2，n2),B2(0，0),C2(p2，q2).则有

图1

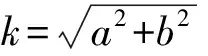
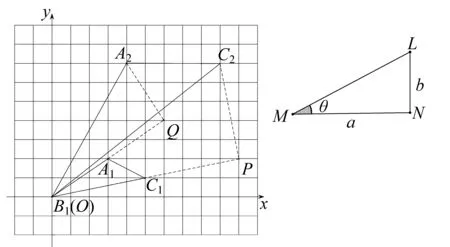
图2

证明△A2B1C2的作法如下：

(1)延长B1C1至点P,使B1P=aB1C1,显然P为格点;

(2)作PC2⊥B1P(∠PB1C2为逆时针方向),且使PC2=bB1C1,易知C2也为格点;

(3)延长B1A1至点Q,使B1Q=aB1A1,显然Q为格点;

(4)作QA2⊥B1Q(∠QB1A2为逆时针方向),且使QA2=bB1A1,易知A2也为格点;

(5)格点三角形A2B1C2即为所求.

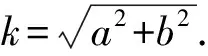
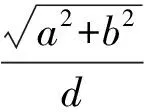
定义已知△A0B0C0是一个格点三角形.若对任意的与它相似的格点△A1B1C1，都有相似比k≥1,k∈R，则称△A0B0C0为一个最小格点三角形.

定理3若△A1B1C1是任意一个格点三角形,则存在最小格点的△A0B0C0,使得△A1B1C1∽△A0B0C0.

定理4设△ABC是格点三角形，且AB2,BC2,AC2被素数r整除，则

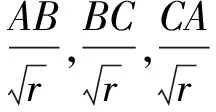
为证明定理4，先给出一个引理.

引理13(1)方程x2≡-1 (modr)对素数r=4k+1有两个解，对r=2有一个解，对素数r=4k+3没有解；

(2)若素数r=4k+3整除x2+y2，则rx,ry.

下面证明定理4：

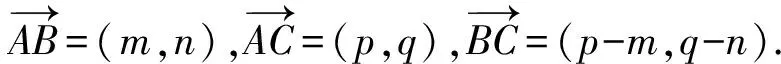
(Ⅱ)若r=2或r=4k+1,-1是r的二次剩余，在模r意义下，有±i两个整数满足x2≡-1,(r=2时，只有一个数1满足)我们知道，若m2+n2≡0(modr),则必有m+ni≡0或m-ni≡0(modr).

下面证明，可以恰当地选取i(必要时用-i替换i)使得同时有

m+ni≡0且p+qi≡0(modr).

为此，首先设m,n,p,q与r互素，因为若m,n被r整除，则同时有m+ni≡0和m-ni≡0(modr),结论便成立了.

又可设r≠2,因为r=2时i≡-i(modr),结论亦成立.

最后，我们设m+ni≡0(modr)但p-qi≡0(modr),此时,有

0 ≡(p-m)2+(q-n)2

≡p2+q2+m2+n2-2pm-2qn

≡0+0-2(iq)(-in)-2qn

≡-4qn≠0(modr).矛盾！

于是，设m+ni≡0且p+qi≡0(modr),

因为r=2,或r=4k+1，

所以r可以表示为a2+b2.

由于a+bia-bi≡0(modr)，

即a+bib+ai≡0(modr)，

所以，不妨设a+bi≡0(modr),否则，交换a,b即可，此时，

am+bn≡0，an-bm≡0,ap+bq≡0,

aq-bp≡0(modr)，

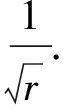
由定理4容易得到：

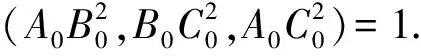
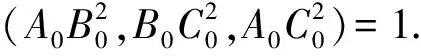
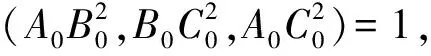
设B0(0,0)，A0(m0,n0)，C0(p0,q0)，

B1(0,0).A1(m1,n1)，C1(p1,q1)，

解得

(Ⅰ)当a=0,b≠0或b=0,a≠0时，

不妨设a=0,b≠0，有

设b=tb0，d=td0，t∈N*，b0,d0=1，

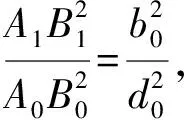
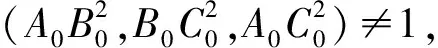
与已知矛盾，所以此时△A0B0C0是最小格点三角形.

(Ⅱ)当a≠0,b≠0时，

令a=ha0，b=hb0，h∈N*，a0,b0=1，

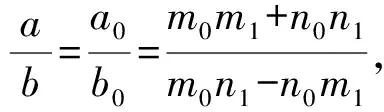
所以m0m1+n0n1=ta0，

n0m1-n0m1=tb0，t∈N*.

设h=lh0，d=ld0，l∈N*,h0,d0=1，

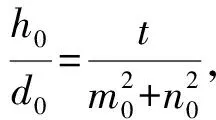
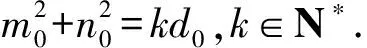
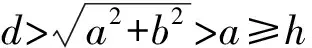
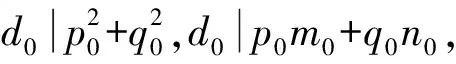
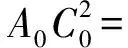
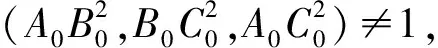
所以此时△A0B0C0是最小格点三角形.

综上可得，△A0B0C0是最小格点三角形.

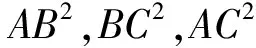
d=(AB2,BC2,AC2),(d≠1)，

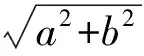
为证明定理6和7，再给出两个引理：

引理23正整数n可以表示成两个整数的平方和当且仅当n的每个形如4k+3的素因子的重数是偶数．

引理3若x=m2+n2，y=p2+q2，则x,y的公因数d可以表示成a2+b2的形式．

证明由于x=m2+n2，y=p2+q2，由引理2知，x,y的每个形如4k+3素因子的重数是偶数，所以d的每个形如4k+3的素因子的重数也是偶数，故d可以表示成a2+b2的形式.

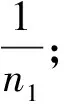
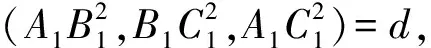
基于以上定理以及推论，下面来解决文首提出的问题：