500kV／220kV四回路复合横担塔多尺度有限元分析*

龙海波 段松涛 孙清 宁帅朋 赵雪灵

（1.中国能源建设集团江苏省电力设计院有限公司 南京211102；2.中国电力顾问集团电规总院 北京100120；3.西安交通大学土木工程系 710049）

引言

输电杆塔是承受导线、地线、绝缘子串和自身荷载的支撑构件，其力学性能直接影响着输电线路的安全性、可靠性和经济性。目前对输电塔的结构计算分为以下两类：（1）基于杆系模型、壳模型及实体模型等宏观模型的整体结构非线性计算；（2）基于壳单元、实体单元的复杂构件及节点局部结构的非线性计算。但随着技术的发展，上述两类计算仍存在以下不足：对于梁杆模型，虽然计算量小，但很难反映结构的真实破坏机理，比如构件的局部破坏特征、节点局部破坏以及法兰连接处等；而对于壳和实体单元模型，虽能较好地反映局部结构的破坏特征，但由于计算机条件的限制，故对实际结构完全采用多尺度模型是不现实的，更重要的是仅对局部构件进行多尺度分析很难精确地确定连接的边界条件，导致计算结果与实际存在差异[1，2-5]。因此对输电塔的计算迫切需要一种既能反映整体结构力学行为又能模拟局部节点受力情况的计算模型。对于实际工程结构采用多尺度计算主要是分析模型的不同部分采用不同尺度，目的是为了取得较高的计算精度的同时提高计算效率，例如：对受力复杂的节点和构件采用实体单元来分析其开裂、局部失稳及屈曲等非线性行为，而对于受力简单的构件采用梁单元，通过选择合理的界面连接形式，保证宏观模型和局部模型的变形协调性，准确地反映整体受力特性和局部的破坏过程[1，6-12]，因此，既可以反映其实际受力特性又可降低计算量。

本文利用ANSYS有限元软件中的MPC法（Multiple point constraint）建立约束方程，实现了多尺度模型和梁杆模型连接界面的协调性。计算结果表明，这种方法能准确模拟结构的受力情况，应用性更强，将其运用于输电塔结构的分析具有很重要的工程意义。

1 多尺度模型界面连接原理

合理地选择多尺度模型的连接界面是多尺度模型计算的关键。在实际工程结构中，经常需要采用杆单元、梁单元、壳单元以及实体单元建立模型，但不同类型的单元自由度可能不同，因此连接界面处应遵循不改变自由度数目的原则，单元自由度异同包含两个含义，即单元自由度个数及其物理意义。当不同类型的单元自由度相同时，采用共用节点；当不同类型单元的自由度不同时，则需要建立约束方程[1，13]。约束方程是一种联系自由度的线性方程，形式如下：

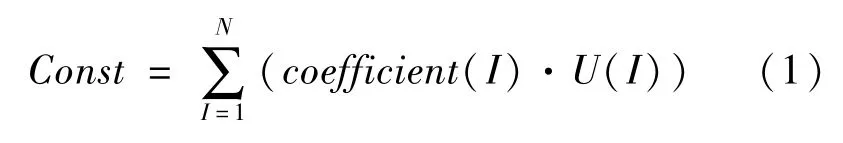
式中：U（I）为自由度项；Coefficient（I）为自由度项U（I）的系数；N为方程中项的编号。即不同单元的节点连接部位建立自由度间的关系方程，从而保证节点间的线位移和角位移的协调性。本文选取在界面上自动生成约束方程，但要精确选择出界面节点，MPC法利用MPC184刚性单元，该单元通过设置可以模拟刚性杆、刚性梁、滑移约束等运动形式，且该单元支持大位移等非线性行为[1，13]。图1为一个钢管的多尺度模型和梁单元模型，由于钢管是空心结构，因此在壳单元中心建立一个节点，通过编制一个利用MPC184单元形成刚性域的循环命令流，最后将梁直接与中心节点相连，如图1b所示。图1a为全梁有限元模型，图1c为开启单元截面显示后的多尺度模型。

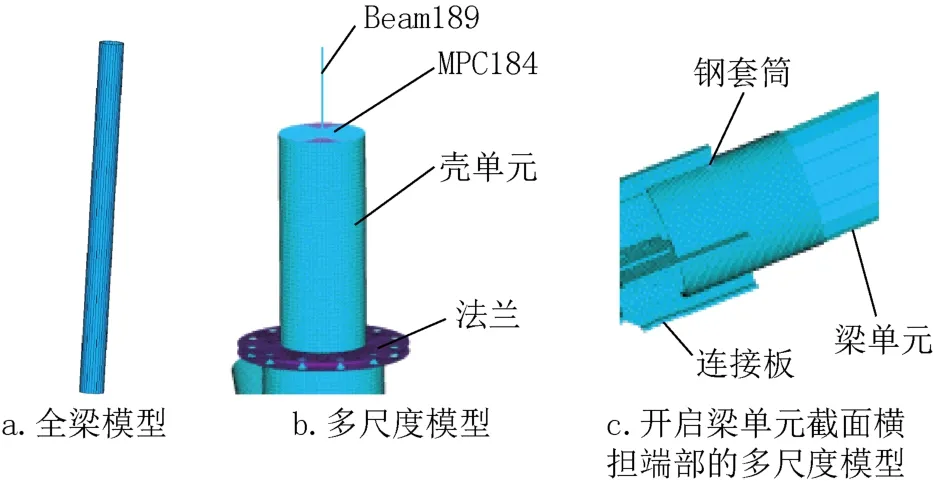
图1 多尺度模型和梁单元模型Fig.1 Multi-scale model and element model

2 多尺度模型建立和校核

以500kV／220kV混压四回路复合横担FH-20钢管塔为研究对象，该塔主要由钢管和角钢组成，主材采用Q460，斜材采用Q345，辅材采用Q345和Q235，塔腿高9m，呼高36m，全高79.5m。FH-20的设计条件为：（1）地线型号：JLB20A-150，1，2回路电压等级为500kV，导线型号为：4×JL／G1A-630／45钢芯铝绞线，3，4回路电压等级为220kV，导线型号为：2×JL／G1A-630／45 钢芯铝绞线；（2）基本风速为29m／s，覆冰厚度导线5mm、地线10mm；（3）水平档距为500m，垂直档距为650m。

由于塔身节点和横担端部节点受力复杂，因此分别以塔身节点（630）和横担端部节点（530）的多尺度模型为研究对象，建立模型步骤如下：（1）首先采用壳单元建立塔身和横担端部节点，如图2所示，塔身节点模型共计106936个单元，横担端部节点模型共计54880个单元；（2）塔身节点和横担端部节点在整塔中是以一定角度和相应的位置连在整个结构中，故在整塔单线模型（刚架模型）中建立局部坐标系，以部件形式导入替换掉原来的塔身节点的单线模型，共计162986个单元；（3）用MPC法建立多尺度连接，组装后的模型如图3所示。同时建立了FH-20输电铁塔的梁杆混合模型（图4），目的是验证多尺度模型的合理性。梁杆混合模型是指铁塔的主材、横隔材及斜材视为梁单元，辅材视为杆单元。

为验证复合横担输电塔多尺度模型的合理性，分别对梁杆模型和多尺度模型进行模态分析，并对同一荷载工况下塔头位置处的位移进行对比。表1、表2和图5分别为多尺度模型与梁杆模型前几阶频率和60°大风工况下塔头位移的比较，通过对比可以看出多尺度模型频率稍小于梁杆模型，其原因是多尺度模型中钢节点和钢套管的加入增大了塔的质量，从而使频率减小；二者塔头位移相差仅为0.37%。

图2 节点多尺度模型Fig.2 Multi-scale model of node

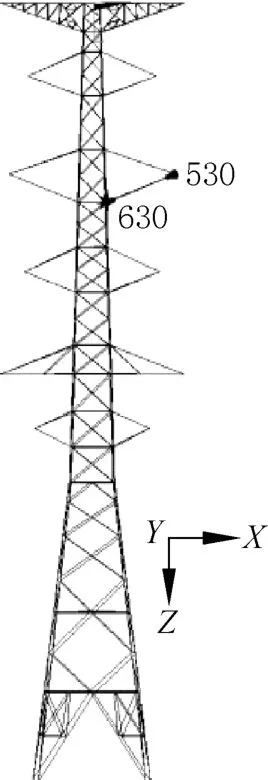
图3 多尺度模型Fig.3 Multi-scale model

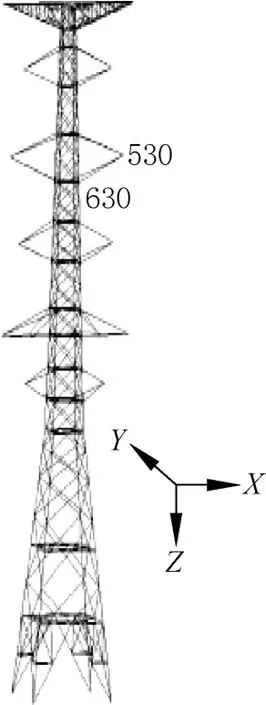
图4 梁杆模型Fig.4 Truss-framed model

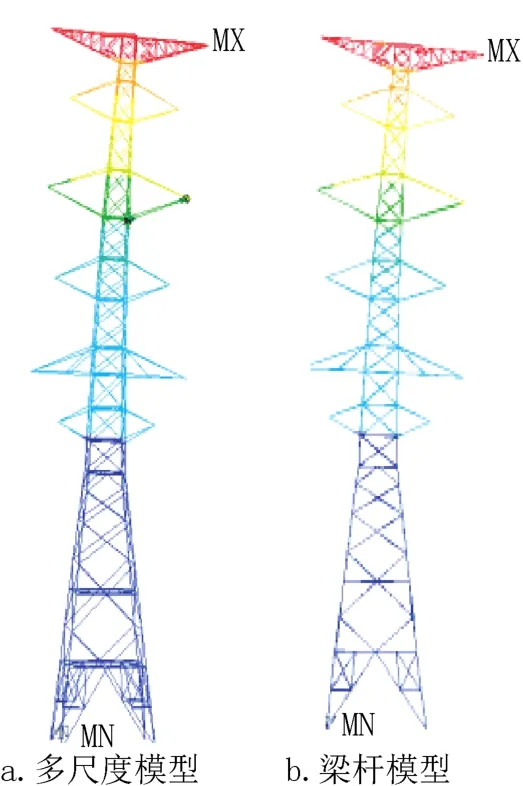
图5 位移云图Fig.5 Displacement cloud imagery

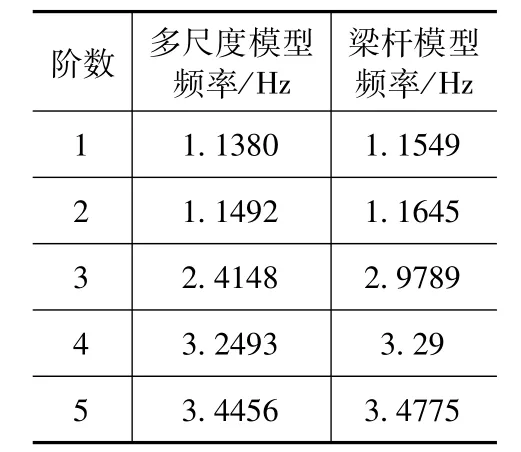
表1 自振频率对比Tab.1 Comparison of the frequency

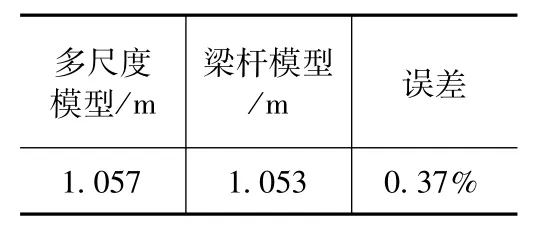
表2 位移对比Tab.2 Comparisons of displacemen

3 节点多尺度非线性分析

将采用壳单元建立的实体塔身节点（630）及横担端部节点（530）运用MPC184法和公式（1）的原理装入整塔，并建立整塔多尺度有限元模型。对装入节点的整塔结构进行非线性静力分析，重点分析节点的受力及变形，同时对比分析梁杆模型和多尺度模型支座反力、主材及横担构件的内力。

3.1 受力及变形分析

1.60°大风工况

由图6可得630节点在该工况下法兰螺栓孔由于应力集中，应力最大达到661MPa，应变达到3174με，螺栓受拉时受到撬力，经验算螺栓抗拉连接强度满足《钢结构设计规范》（GB 50017-2012）[14]承载力要求。

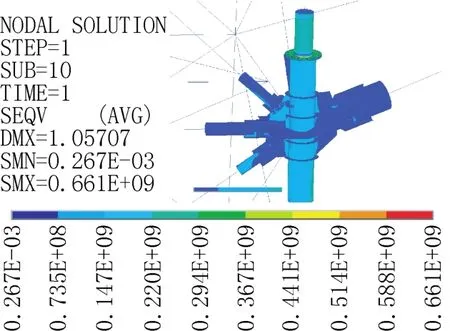
图6 630节点应力云图Fig.6 Stress cloud imagery of 630 node

由图6可得塔身630节点在该工况下法兰螺栓孔由于应力集中，应力最大达到661MPa，应变达到3174με，螺栓受拉时受到撬力，经验算螺栓抗拉连接强度满足《钢结构设计规范》（GB 50017-2012）[14]承载力要求；由图7 可得2回路中横担压杆应力最大为35.8MPa，出现在横担压杆和塔身连接处，拉杆应力最大为247MPa，出现在横担左边端部，均小于复合材料抗拉和抗压设计值，具有较大的安全储备。

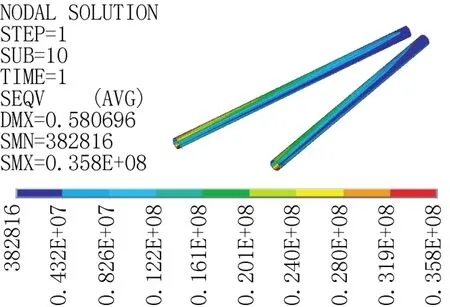
图7 横担压杆截面应力云图Fig.7 Stress cloud imagery of cross-bore

2.断1回地线，上导，中导工况

断线对横担压杆影响较大，该工况下横担端部530节点中间十字水平连接板处螺栓孔由于应力集中，应力最大达到422MPa，应变达到205με，由于塔身630节点处上部主材截面减小，引起应力集中，在上部主材与法兰连接处出现最大应力为375MPa，应变达到1820με。由图8可得2回路中横担压杆应力最大为60MPa，拉杆应力最大为370MPa，出现在横担压杆和塔身连接处，均小于复合材料抗拉和抗压设计值，设计具有较大的安全储备。

3.断1回地线，中导，下导工况

该工况下630节点处螺栓孔由于应力集中，应力最大达到373MPa，应变达到1846με，530节点中间十字水平连接板螺栓孔应力最大达到332MPa，应变达到1641με，而压杆的轴力为114.2kN，根据《钢结构设计规范》（50017-2012）[14]对螺栓群进行抗剪验算，满足承载力要求。由图9可得1回路横担压杆应力最大为54MPa，2回路拉杆应力最大为321MPa，出现在横担压杆和塔身连接处。

4.正锚4回中导，已锚1，2回，3，4回上导，3回中导工况

由图10可得530节点拉杆与节点板连接处由于应力集中，应力最大达到335MPa，应变达到1846με；安装工况对横担拉杆受力影响较大，由图11可得2回路拉杆应力最大为325MPa，1回路中横担压杆应力最大为33.4MPa，出现在横担压杆和塔身连接处，但均小于复合材料设计值。

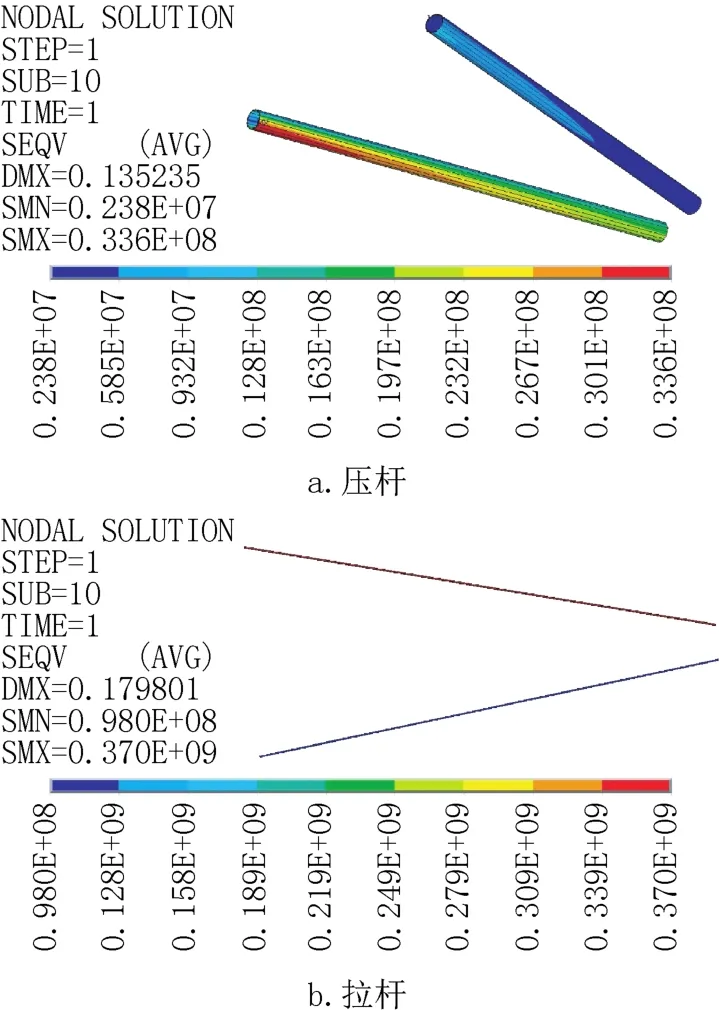
图8 横担截面应力云图Fig.8 Stress cloud imagery of cross-bore

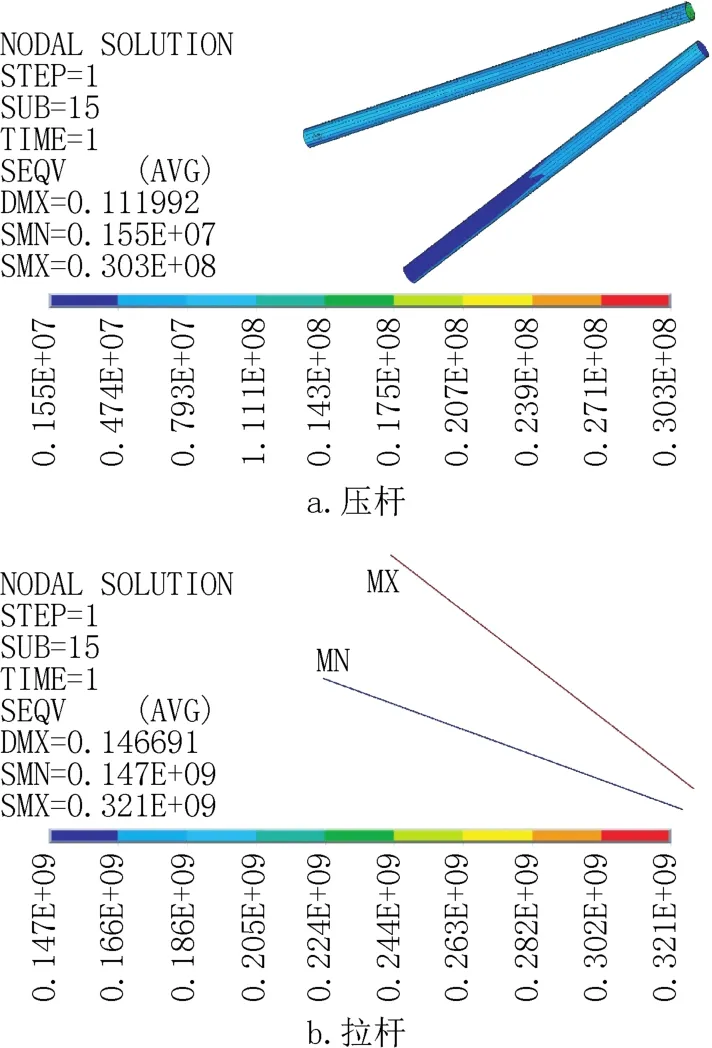
图9 横担截面应力云图Fig.9 Stress cloud imagery of cross-bore

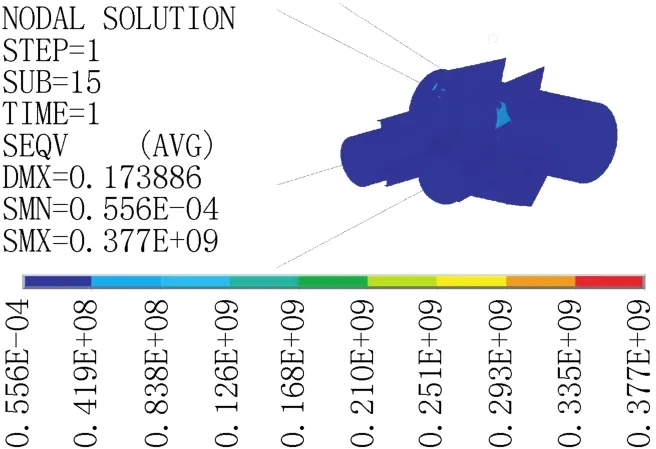
图10 530节点应力云图Fig.10 Stress cloud imagery of node

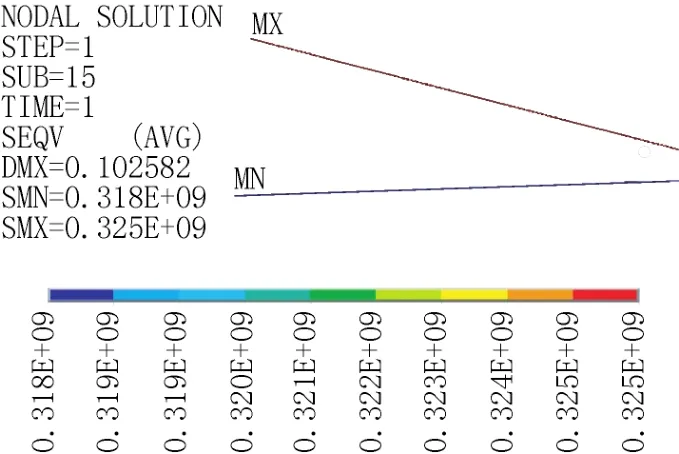
图11 横担拉杆截面应力云图Fig.11 Stress cloud imagery of cross-bore

3.2 静力分析与总结

对以上4个控制工况进行多尺度和梁杆模型的静力对比分析，表3为各个工况下1，2回路中横担拉杆和压杆轴力、弯矩的对比，表4为各个工况下塔头位移、主材轴力及支座反力对比。

对比分析表3和表4中多尺度模型和梁杆模型输电塔的塔头位移、主材轴力及横担轴力及弯矩得出以下结论：

（1）多尺度模型的横担拉杆和压杆的内力与梁杆模型的横担在同一工况下的内力比较，二者相差很小；

（2）梁杆模型和多尺度模型在两个断线工况下塔头最大位移发生的位置及数值是相同的，而在60°大风和安装工况下梁杆模型与多尺度模型相比塔头位移分别相差0.37%和1.1%；

（3）塔腿竖向支座反力在60°大风和断1回地线，中导，下导工况下压力减小，其他工况均增大，而支座反力拉力均增大；

（4）塔腿上部第一段主材和变坡处主材轴拉力均增大，轴压力均减小，经验算拉杆和压杆的强度和稳定均满足要求。

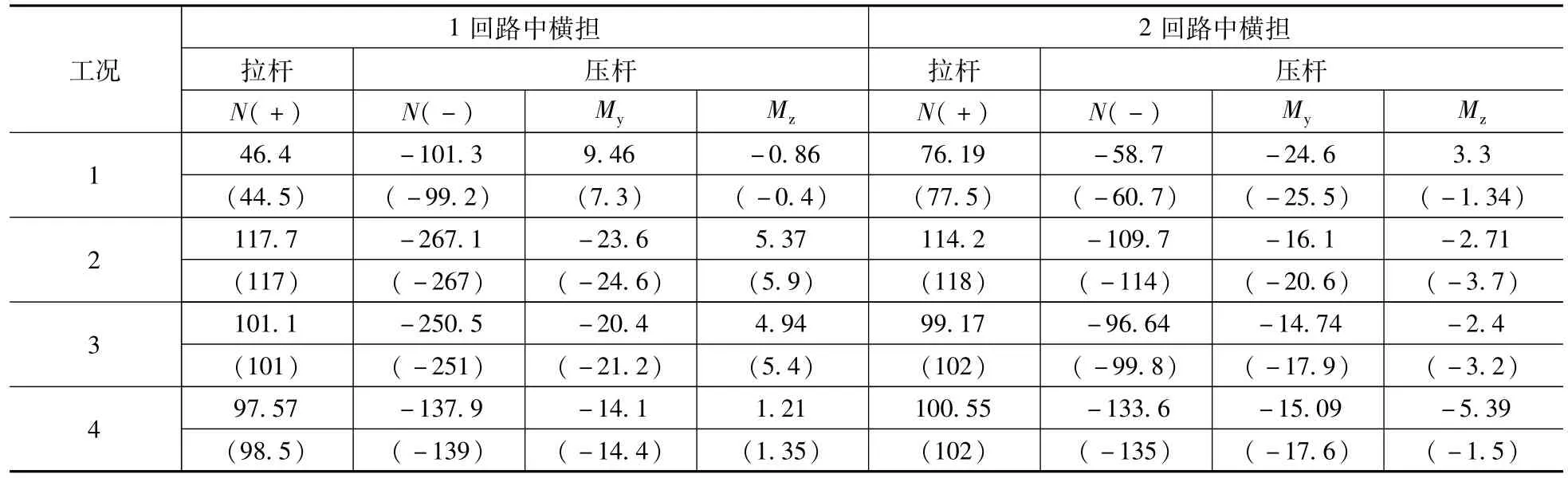
表3 内力对比Tab.3 Comparisons of internal force

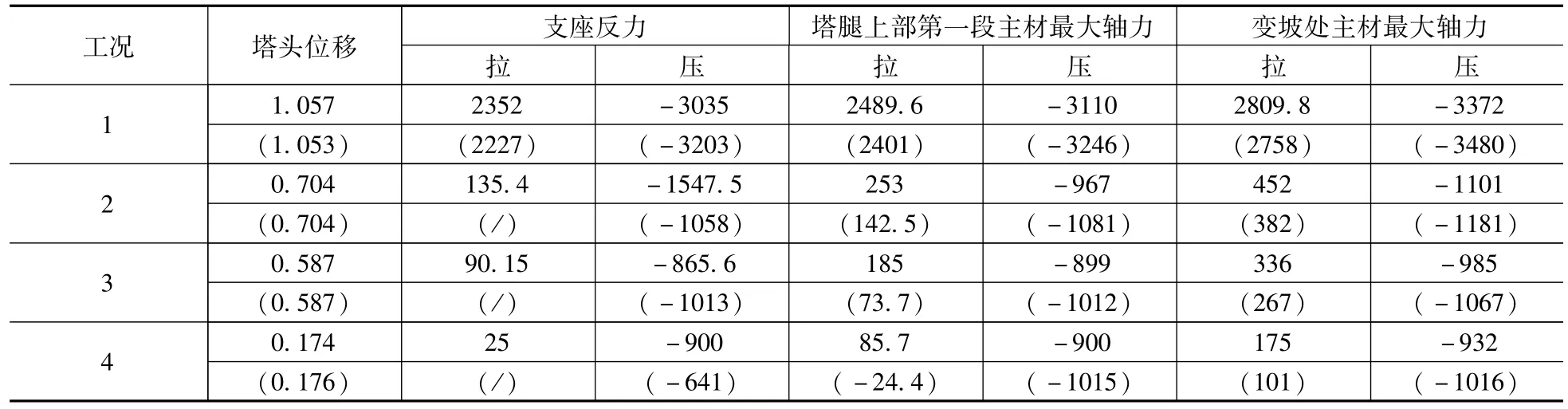
表4 位移和内力对比Tab.4 Comparisons of force and displacement

4 结论

本文通过引入约束方程将壳单元的节点模型和梁杆模型进行连接，从而建立了多尺度模型，并且校核了多尺度模型的合理性，得出以下结论：

1.对于多尺度模型引入约束方程成功地连接了壳单元和梁单元的模型，保证了变形协调和力的有效传递。

2.对比分析多尺度模型和梁杆模型的前五阶频率、振型以及塔头位移，验证了多尺度模型的合理性。

3.塔身节点在大风工况下法兰连接螺栓孔处应力最大，而在断线工况下横担端部节点十字连接板螺栓孔应力最大，其值分别为661MPa和420MPa，因此应注重法兰连接的设计；横担压杆截面最大应力为60MPa，拉杆的最大拉应力为370MPa，具有较大的安全储备性。

4.多尺度计算方法计算精度高且计算代价低，能真实地反映节点局部受力特征、局部开裂以及屈曲的非线性行为，可以广泛应用于工程结构计算中。