剪切变形状态下压杆稳定临界力分析

崔海军

（扬州工业职业技术学院，江苏 扬州225127）

0 引言

受压杆件的稳定性计算是工程结构中常见的分析问题［1］，如桥梁结构中的桁架和高桥墩、钢结构工程中的斜梁、立柱［2］和支撑体系［3］、岩土工程中的钻杆［4］以及工程建设中的脚手架杆件［5］。材料力学临界力欧拉公式是在中心受压直杆理想压杆模型［6-7］、剪切变形忽略假定下推导的［8］。但由于杆件的初始曲率、竖向作用的初始偏心以及水平作用，必然导致压杆的剪切变形［8］。

在以往文献中，压杆的临界力按不同的约束条件，从压杆的挠曲线近似微分方程求解，方法繁琐，也不能全部推导证明［9］。文献［10-11］利用弯矩微分方程和力的边界条件推导了理想压杆临界力的欧拉公式，形成统一公式，简化了推导过程［10-11］，但压杆的稳定问题的实质是整体变形效应问题，用力的边界条件求解容易出现不确定和解的不一致问题［12］。文献［9］以一端固定，一端铰支的细长压杆挠曲线微分方程推导了理想压杆临界力的欧拉公式，体现了杆的整体变形效应［9］，但压杆的挠曲位移仅为弯曲位移，没有考虑剪切变形引起的位移，且压杆失稳模型上端铰支，与不同约束条件下压杆实际屈曲状态不完全吻合。与文献［9-11］不同，本文以细长压杆在弯曲变形和剪切变形下平衡条件建立其挠曲线微分方程，推导不同约束边界条件下考虑剪切变形影响下压杆临界力公式。

1 基本算式

如图1所示，一发生剪切变形的细长受压杆，下端固定，上端在平面内自由。细长杆件受压力F，同时在自由端附加一水平作用力FR，代替实际杆件在杆件上端可能受到的水平支反力，以及附加一外力偶MR，代替实际杆件在杆件上端可能受到的约束外力偶。压杆弹性模量为E，横截面惯性矩为I，剪切模量为G，横截面积为A，自由端在平面内微弯形态下平衡时最大水平位移为δ，建立图示坐标系，则细长压杆在垂直于轴线的总位移W（x）可表示为：

式中，wf（x）为弯曲变形引起的位移，ws（x）为剪切变形引起的位移。取距离细长压杆下端x的截面，该截面的转角为 φ（x），则 φ（x）为：

由材料力学知：

对于剪力Q（x），在文献［12］按下式方法一选取：

在文献［13-14］按下式方法二选取：

但是，在挠度变形问题中，sin［φ（x）］＝φ（x）偏差较大，一般不再成立。所以，方法二剪力取值既不适用于小挠度变形问题，也不适用于大挠度变形问题，仅适用于文献［13-14］中所阐述的橡胶材料的临界力计算。本文按照方法一进行考虑剪切变形状态下的压杆临界力分析。

对于方法一：

式中，V为截面形状系数，矩形截面取6/5，圆形截面取10/9。对于V的取值，文献［16］尚有异议，因此，也有文献取V为1，即忽略截面形状系数。

对式（1）两边进行求导，并将式（2）和式（8）代入得：

由式（9）得：

对式（10）两边进行求导得：

将式（3）和式（4）代入式（11）得：

解此微分方程，通解为：

则w（x）的一阶导数为

由式（9）及式（15）得：

图1 压杆计算模型

图2 两端铰支压杆失稳模型

2 几种杆端约束形式下考虑剪切变形的细长压杆的临界力

2.1 两端铰支的压杆

如图2所示，对于两端铰支的压杆，δ＝0，MR＝0；由于压杆上端水平支反力FR与下端水平支反力要平衡，构成力偶，但杆件不受外力偶作用，因此FR＝0。位移边界条件为：x＝0，w＝0；x＝l，w＝0。将边界条件 x＝0，w＝0代入式（14）得：

B＝0

将边界条件 x＝l，w＝0代入式（14）得：

A sin kl＝0

因为B＝0，A与B不可能同时为0，即A不等于0，则

sin kl＝0

由此求得 kl＝nπ，n＝0，1，2…

根据工程实际问题，取n＝1，将k代入式（13）得压杆临界压力

式中

在式（17）中，当剪切刚度＝∞时

即为不考虑剪切变形时的欧拉公式。

2.2 一端固定，一端自由的压杆

如图3所示，对于一端固定，一端自由的细长压杆，自由端不能提供水平支反力及约束力偶，因此FR＝0，MR＝0。位移边界条件为：x＝0，w＝0，φ＝0；x＝l，w＝δ。将边界条件 x＝0，φ＝0代入式（16）得：

故A＝0

将FR＝0及位移边界条件x＝0，w＝0代入式（14）得：

B＝-δ

将 x＝l，w＝δ代入式（14）得：

δ（1-cos kl）＝δ

则能使细长压杆挠曲线成立的条件是：

cos kl＝0

从而得到

kl＝nπ/2，n＝1，3，5…

其最小解为n＝1，将k代入式（13）得压杆临界压力

式中

在式（20）中，当剪切刚度＝∞时

即为不考虑剪切变形时的欧拉公式。

2.3 两端固定的压杆

如图4所示，对于两端固定的压杆，δ＝0；由于两端固定压杆边界约束、所受外力、变形对压杆中点上下对称，压杆两端所受约束外力偶相互平衡，而压杆上端水平支反力FR与下端水平支反力要平衡，构成力偶，但杆件除固定端约束外力偶作用，不受其它外力偶作用，因此FR＝0（也可以根据对称条件，水平支反力对压杆中点反对称，直接判断水平支反力 FR＝0）。位移边界条件为：x＝0，w＝0，φ＝0；x＝l，w＝0，φ＝0。

图3 一端固定、一端自由压杆失稳模型

图4 两端固定压杆失稳模型

将位移边界条件x＝0，φ＝0代入式（16）得

故A＝0

将位移边界条件x＝0，w＝0代入式（14）得：

将位移边界条件 x＝l，w＝0，φ＝0代入式（14）、式（16）得：

由此求得 kl＝2nπ，n＝0，1，2…

根据工程实际问题，取n＝1，将k代入式（13）得压杆临界压力

式中

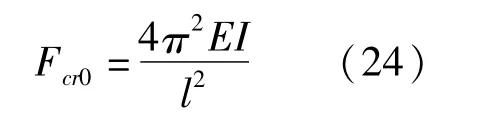
在式（20）中，当剪切刚度＝∞时

即为不考虑剪切变形时的欧拉公式。

2.4 一端固定、一端铰支的压杆

如图5所示，对于一端固定、另一端铰支的压杆，δ＝0；上端铰支座端不能提供约束力偶，因此MR＝0；下端固定端有约束外力偶，这就要求压杆上端铰支座提供水平支反力FR，以平衡固定端约束外力偶。位移边界条件为：x＝0，w＝0，φ＝0；x＝l，w＝0。

将位移边界条件x＝0，w＝0代入式（14）得：

由压杆受力特征分析知，压杆下端剪力为-FR，则由式（5）、式（15）可得：

将位移边界条件x＝l，w＝0代入式（14）得：

A sin kl+B cos kl＝0

将A、B代入上式得

tan kl＝kl

上式为超越方程，利用三角函数表或采用图解法求解，求得最小正数值解

kl＝4.49

将k代入式（13）得压杆临界压力

式中

在式（26）中，当剪切刚度＝∞时

即为不考虑剪切变形时的欧拉公式。

图5 一端固定、一端铰支压杆失稳模型

图6 一端固定、一端定向支撑压杆失稳模型

2.5 一端固定、一端定向支撑的压杆

如图6所示，一端固定、一端定向支撑的压杆，即为两端固定但可沿杆件横向相对移动，因此FR＝0。根据杆件受力及变形的对称性，对称截面w（x/2）＝δ/2，M（x/2）＝0，则由式（4）得：

对于一端固定、一端定向支撑的压杆，位移边界条件为 x＝0，w＝0，φ＝0；x＝l，w＝δ，φ＝0。

将位移边界条件 x＝0，w＝0及式（29）代入式（14）得

将位移边界条件x＝0，φ＝0及式（28）代入式（16）得 A＝0

将位移边界条件x＝l，w＝δ代入式（14）得

coskl＝-1

从而得到

其最小解为n＝0，将k代入式（13）得压杆临界压力

式中

在式（30）中，当剪切刚度＝∞时

即为不考虑剪切变形时的欧拉公式。

3 考虑剪切变形状态下压杆临界力统一公式

由2.1～2.5五种不同约束条件下考虑杆件剪切变形状态下压杆临界力分析，其压杆临界力公式可以统一写成

Fcr表达式与材料力学欧拉公式一致，为长度因素，两端铰支，μ＝1，一端固定、另一端自由μ＝2，两端固定μ＝0.5，一端固定、另一端铰支μ＝0.7，一端固定、另一端定向支撑μ＝1

4 结论

（1）提出了一端固定、另一端平面内自由的细长压杆考虑剪切变形下压杆失稳计算模型。

（2）对计算模型在剪切变形和弯曲变形平衡条件下推导细长压杆统一的挠曲线方程w（x）和转角方程φ（x），w（x）由弯曲位移和剪切位移两部分组成，φ（x）为弯曲位移方程的一阶导数。

（3）针对五种约束条件下的压杆，利用统一的挠曲线方程w（x）和转角方程φ（x）推导了考虑剪切变形状态下压杆稳定的临界力公式及统一公式。