配筋钢管混凝土构件抗弯承载力计算方法研究*
朱铨雯 刘嘉 童华炜 张绍斌 袁杰
(1.广州大学土木工程学院 510006;2.中交第四航务工程局有限公司 广州510290)
引言
由于钢管的约束作用,配筋钢管混凝土柱具有优良的抗压承载力,目前在国内外已经得到了广泛应用[1,2]。截至目前,对配筋钢管混凝土构件的研究主要集中在轴压承载性能方面,如林沁[3]等通过偏压作用下椭圆钢管混凝土短柱的参数分析和数值分析拟合了轴力-弯矩相关曲线;余敏[4]等在收集大量的试验数据的基础上,给出了规范中圆形及方形钢管混凝土构件轴压承载力设计公式以及方形钢管混凝土构件轴压承载力设计公式的计算模式不确定性的统计参数;沈奇罕[5]等分析了轴压作用下椭圆钢管混凝土短柱的诸多参数,提出了椭圆钢管混凝土短柱的轴压承载力简化计算公式;陈志华[6]等通过对配螺旋箍筋方钢管混凝土柱进行参数化分析,推导了适用于配螺旋箍筋方钢管混凝土柱的轴压承载力计算公式;范重[7]等介绍了巨型方钢管混凝土柱正截面与斜截面承载力的计算方法。
然而,尽管在工程实际中较为少见,配筋钢管混凝土构件仍有可能受到拉弯联合作用,如在风荷载及地震荷载作用下的高层结构或输电塔桩基等。但是,鲜有学者对配筋钢管混凝土的拉弯性能进行研究。因此,开展如何计算配筋钢管混凝土构件在拉弯复合受力状态下的承载力研究具有重要的理论和实践意义。本文采用理论研究和数值分析的手段,以配筋钢管混凝土桩在拉弯联合作用下的抗弯承载力为研究目标,结合相关技术规范,提出一种配筋钢管混凝土构件抗弯承载力计算方法,以期为类似构件的设计和推广提供参考。
1 抗弯承载力计算方法
本文抗弯承载力计算方法采用有限条分法,即将试件划分为有限个单元,赋予每个不同类型单元相应的本构关系,利用平衡条件,求得试件的承载力。具体如下述。
1.1 计算模型简化
为了便于表示和计算,将配筋钢管混凝土的纵向受力钢筋等效为圆环。等效原则为钢筋的总面积与圆环的面积相等,所处同心圆位置相同。以大偏心受压为例,简化的计算模型如图1所示。图中:D为桩径;xc为中和轴到桩截面圆心的垂直距离;xr为受压区高度;Ai为单根纵向钢筋的截面积;r0为单根钢筋截面形心到桩截面圆心的距离;t0为等效后圆环的壁厚;α、β为钢管及钢筋对应的受压角。参数取值可根据式(1)~式(3)进行计算:
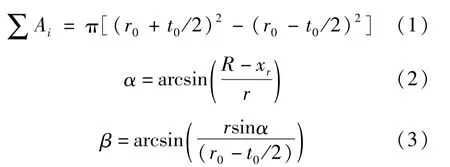
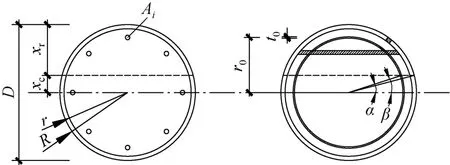
图1 配筋钢管混凝土截面简化计算模型Fig.1 Simplified calculation model of reinforced concrete-filled steel tubular section
1.2 极限状态定义
当受到轴心拉力和弯矩作用时,定义受拉区边缘钢管应变达到εs1,tu时(文献[8]取值为0.01),配筋钢管混凝土达到了承载能力极限状态。当轴心拉力较小时,截面存在受压区,混凝土承担部分弯矩作用,此时为大偏心受拉状态,如图2a所示;当轴心拉力较大时,配筋钢管混凝土全截面受到拉力作用,所有拉力和弯矩作用均由钢管和钢筋承担,此时为小偏心受拉状态,如图2b所示。图中:下标s1、s2分别代表钢管和钢筋,t和c分别代表受拉区和受压区,u代表达到极限应变。
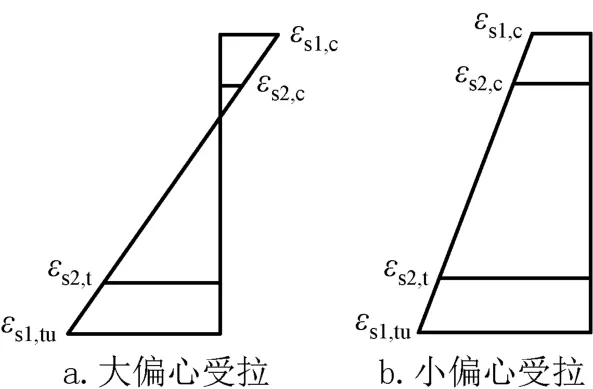
图2 承载力极限状态时截面应变分布示意Fig.2 Schematic diagram of section strain distribution in Ultimate state of bearing capacity
1.3 计算假定
计算过程中采用如下假定:(1)不考虑混凝土的抗拉强度;(2)不考虑钢管与混凝土、钢筋与混凝土间的相对滑移;(3)构件在变形过程中符合平截面假定。
1.4 材料本构
1.钢材本构
我国常用碳素钢和低合金钢的应力-应变曲线一般可分为五个阶段,而本文对其作适当简化,划分为四个阶段,其受力状态如图3所示,各阶段的极限应力及极限应变值见表1。
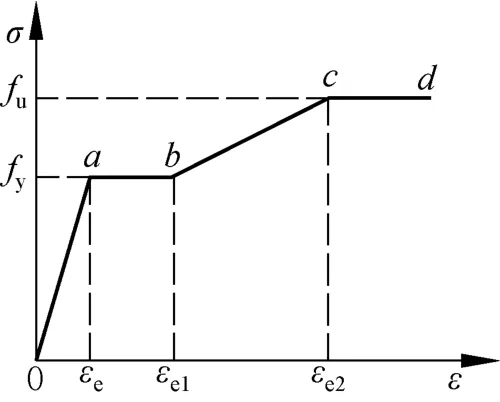
图3 钢材本构曲线示意Fig.3 Schematic diagram of the constitutive curve of steel
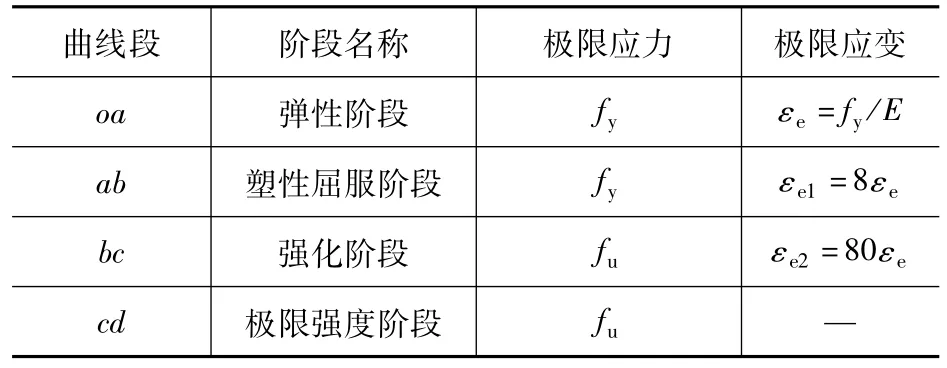
表1 各阶段钢材应力应变取值Tab.1 Stress-strain values of steel in various stages
2.混凝土本构
作为本文的配筋钢管混凝土核心区的混凝土材料模型,其混凝土的本构采用刘威[9]对韩林海[10]修正后的本构模型,具体表达式如式(4)所示:
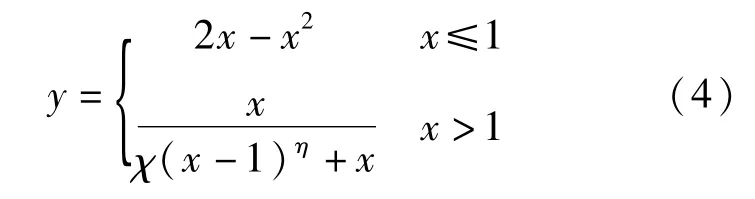
式中:x=ε/ε0;y=σ/σ0;εc= (1300+12.5fc)×10-6,其中fc为混凝土圆柱体抗压强度,以N/mm2为单位;,其中ξ为套箍系数。
混凝土圆柱体抗压强度标准值fck和混凝土圆柱体抗压强度fc的换算关系[10]如表2所示。
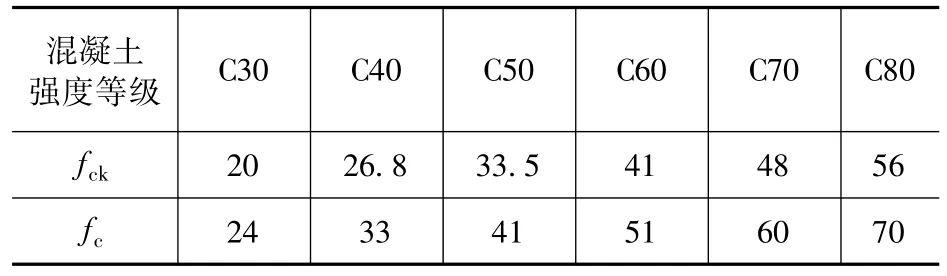
表2 混凝土轴压强度不同表示值之间的近似对应关系(单位:MPa)Tab.2 Approximate relation between different expression values of concrete axial compressive strength (unit:MPa)
1.5 计算步骤
按照受压区高度xr的不同,配筋钢管混凝土的截面应变状态可划分为如图4所示三种不同的情况(对于xr>R的情况在配筋钢管混凝土偏拉构件中不会出现,故没必要进一步划分考虑)。对于大偏心受拉情况,当xr<R-r2时(其中,r2=r0-t0/2),中和轴位于受压区钢管边缘与最外围钢筋之间,钢筋所属区域全部受拉,此时β=π/2;当R-r2<xr<R时,中和轴位于受压区钢筋与形心轴之间,此时xc=R-xr。对于小偏心受拉情况,α和β均取值为π/2。
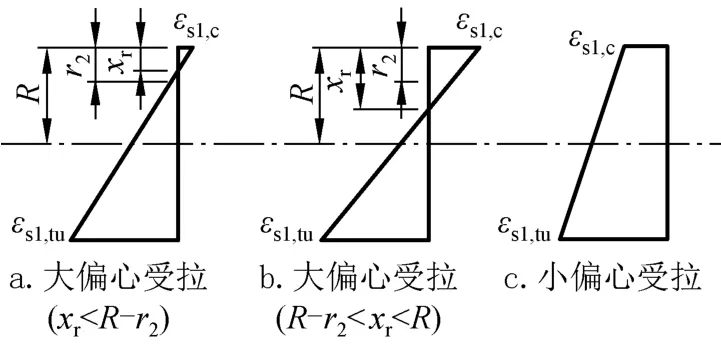
图4 配筋钢管混凝土构件的截面应变示意Fig.4 Sectional strain diagram of reinforced concrete filled steel tubular members
具体计算步骤如下:
1.给定配筋钢管混凝土截面的已知参数,如截面直径D、钢管厚度t、配筋率ρ以及轴拉力T等;
2.将钢筋等效为圆环,计算圆环的等效半径r0和壁厚t0;
3.根据精度需要,确定单元划分的密度。将配筋钢管混凝土截面划分为五个不同的单元区域:受压区混凝土、钢管、钢筋,以及受拉区钢管和钢筋(不考虑混凝土受拉)。对于混凝土区域采用梯形单元划分,而钢管及钢筋则采用弧形单元划分,如图5所示;
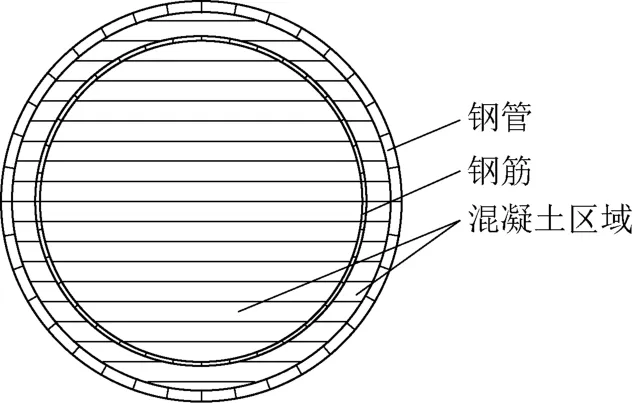
图5 配筋钢管混凝土截面单元划分示意Fig.5 Schematic diagram of sectional element of reinforced concrete filled steel tubular
4.给定受压区边缘钢管初始应变值εs1,c0;
5.判断截面的应变状态:若εs1,c0为负值,则属于大偏心受拉状态,需先利用公式(5)求出受压区的高度,根据xr的值判断中和轴所处的位置,从而判断在该应变值εs1,c0下截面处于图4a、图4b中的哪种应变状态;若εs1,c0为正值,则属于图4c中的小偏心受拉状态;
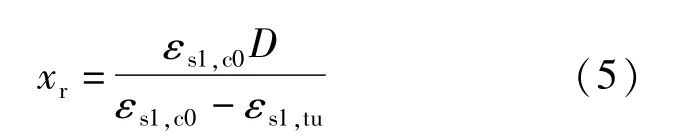
6.利用平截面假定,根据受拉区边缘钢管的极限应变εs1,tu和受压区边缘钢管的初始应变值εs1,c0,推算出任意位置处不同单元的平均应变值(用单元形心处的应变代表单元的应变值);
7.根据求得的平均应变,利用材料本构关系,计算各单元的平均应力值σi;
8.计算各单元的面积:对于混凝土单元,采用矩形公式近似计算;对于钢管和钢筋单元,采用扇形公式计算;
9.利用公式N=∑Aiσi,求出各单元区域承担的合力Nc,c、Ns1,c、Ns2,c、Ns1,t、Ns2,t(第一个下标c、s1、s2分别代表混凝土、钢管和钢筋,第二个下标c、t分别代表受压区和受拉区);
10.利用平衡条件,判断不平衡力的大小:
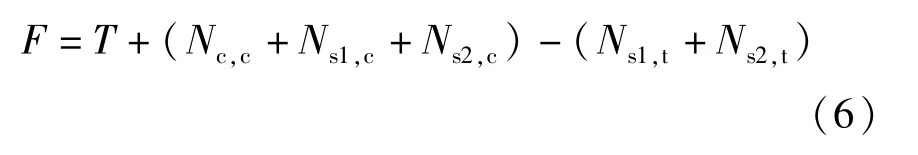
若计算得到的F值与前一次计算的F值同号,用εs1,c代替原来的εs1,c0值(εs1,c的值根据公式εs1,c=εs1,c0+ Δεs1,c进行计算),然后重复步骤5~9;若前后两次得到的F值异号,则认为该εs1,c值为所求极限状态下的受压区边缘钢管的应变值(其中拉应变为负,压应变为正,εs1,c0为负值。当εs1,c< 0 时,为大偏心受拉状态;当εs1,c>0时,为小偏心受压状态。Δεs1可根据精度需要选取,本文使用的计算程序取值为0.0001);
11.根据求得的钢管应变值,重复步骤5~8,求得各单元的Ai、σi;
12.计算各单元距离形心轴的距离Di;
13.根据公式(7),分别求出各部分提供的弯矩Mc,c、Ms1,c、Ms2,c、Ms1,t、Ms2,t:
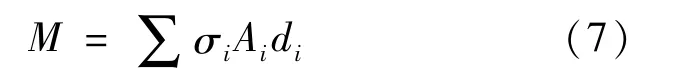
14.将求得的各部分承担的弯矩值叠加,即可得到轴拉力T0下配筋钢管混凝土构件的抗弯承载力Mu:
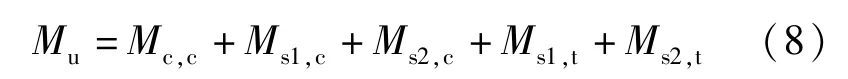
15.指定一系列轴拉力T,重复步骤4~14,即可得到配筋钢管混凝土构件在拉弯联合作用下的极限弯矩M和轴拉力T的关系曲线。
2 M-T曲线的影响因素分析
根据上述的抗弯承载力计算方法,编制了MATLAB计算程序,并通过改变单一参数,定性研究了不同截面参数对M-T曲线的影响规律,如图6、图7所示。图中:M0为纯弯状态下的极限弯矩;Tu为桩体抗拉承载力。根据计算结果,可以得出以下结论:
1.截面直径、钢管厚度、配筋率、钢管及钢筋的屈服强度越大,M-T曲线偏离原点的位置越远,即截面参数取值越大,其抗弯承载力越大。
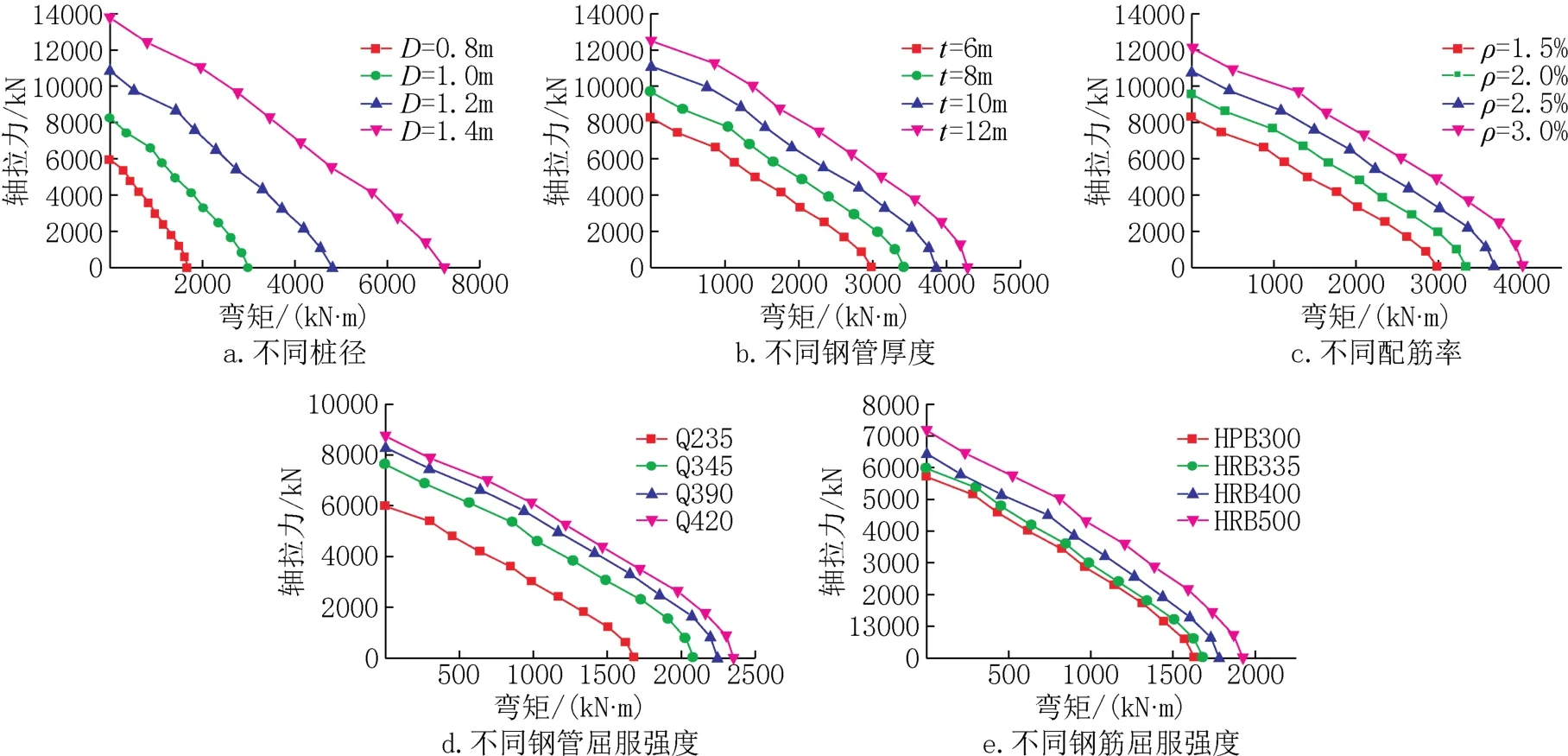
图6 不同因素对M-T曲线的影响Fig.6 Effect of different factors on M-T curve
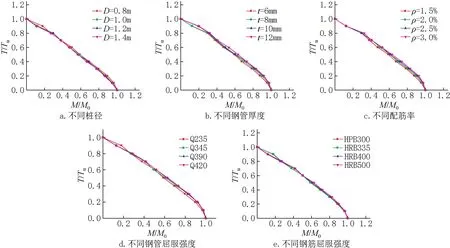
图7 不同因素对M-T归一化曲线的影响Fig.7 Influence of different factors on the normalized curve of M-T
2.截面直径是影响截面抗弯承载力的主控因素。在相同的轴拉力作用下,随着直径的增大,其承载力呈现非线性增长,且增长幅度越来越大;对于钢管厚度、配筋率、钢管及钢材屈服强度而言,随着其取值的增大,承载力呈线性增长。
3.钢管厚度、配筋率及钢管屈服强度越大,M-T归一化曲线朝偏离原点方向的鼓曲程度越大;对于截面直径则相反,其取值越大,M-T归一化曲线朝偏离原点方向的鼓曲程度越小;另外,钢筋屈服强度越大,其对应的M-T归一化曲线朝偏离原点方向的鼓曲程度变化不明显。
3 极限弯矩简化计算方法
要求得配筋钢管混凝土构件的极限弯矩,需要两个关键的已知条件:(1)M-T归一化曲线的表达式;(2)纯弯状态下M0的值。
为此,本节基于常用的桩身参数取值范围(钢管厚度6mm~12mm,截面直径0.8m~1.4m,配筋率1.5% ~3%),共选取64个配筋钢管混凝土构件样本,研究了在该桩身参数取值范围下M-T归一化曲线表达式和M0值的计算方法。
3.1 M-T归一化曲线拟合
选取钢管厚度为6mm、截面直径为1m、配筋率为1.5%、钢管为Q235、钢筋为HRB335时的M-T归一化曲线,如图8所示。观察图中散点的变化趋势可以发现,其变化规律大致呈现二次抛物线形式。根据图中给出的拟合结果可以得知,拟合结果与理论值总体吻合良好。因此,本文采用二次多项式对配筋钢管混凝土构件的M-T归一化曲线进行拟合。
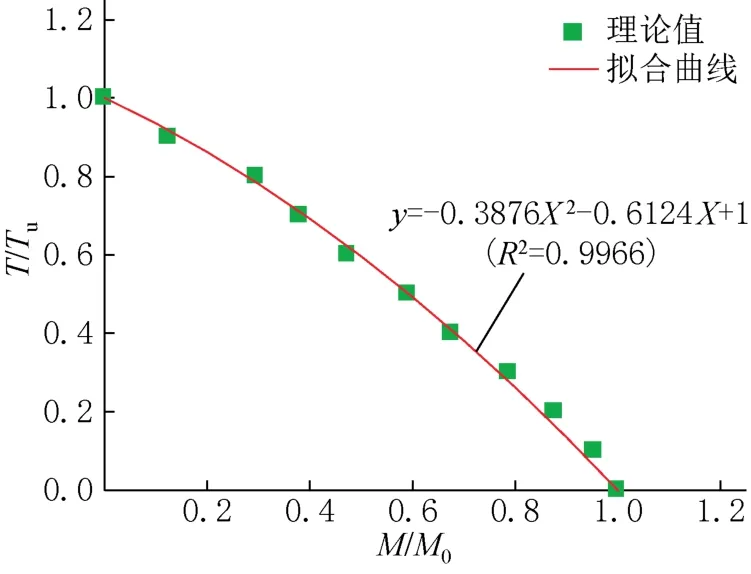
图8 M-T归一化曲线的二次多项式拟合Fig.8 Two-time p olynomial fitting of normalized curve of M-T
如上所述,采用二次多项式对M-T归一化曲线进行拟合,具体的步骤如下:
令x=M/Mu,y=T/Tu,设M-T归一化曲线的形式为:

显然,M-T归一化曲线通过两个固定点(1,0)和(0,1),带入公式(9)可得:
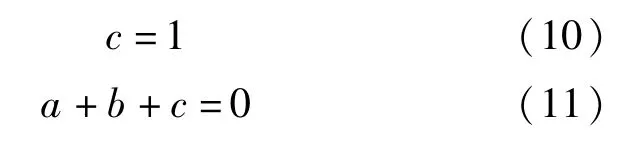
将式(10)和式(11)代入式(9),可以由此得到M-T归一化拟合曲线的基本形式:
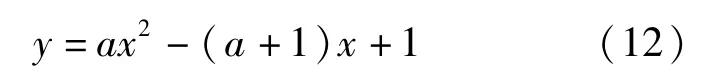
利用最小二乘法可得目标函数F(a):
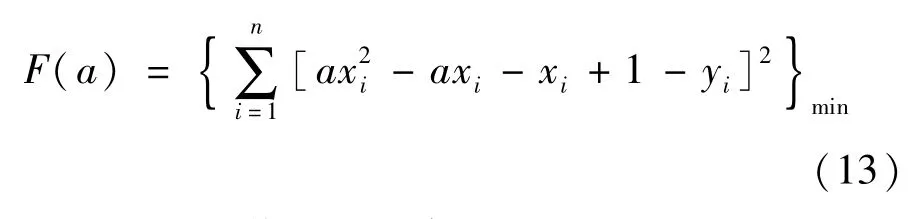
由函数极值的必要条件可得:
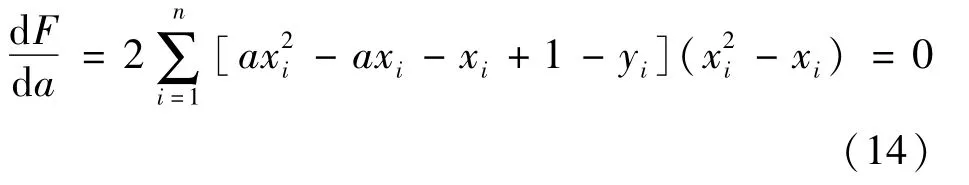
对方程(14)进行化简可得a值的计算公式:
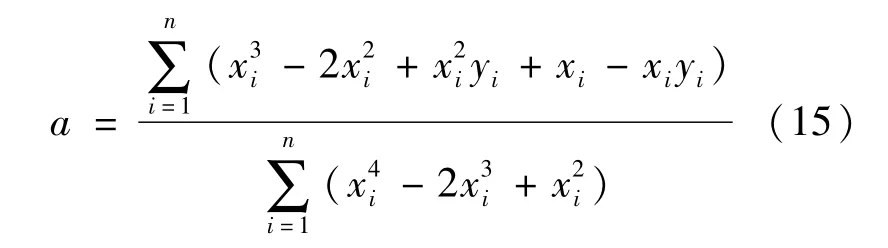
根据公式(15),表3给出了不同桩身参数取值下a的取值,在实际应用中可利用插值法求得本文参数取值范围内任意桩体的a值。
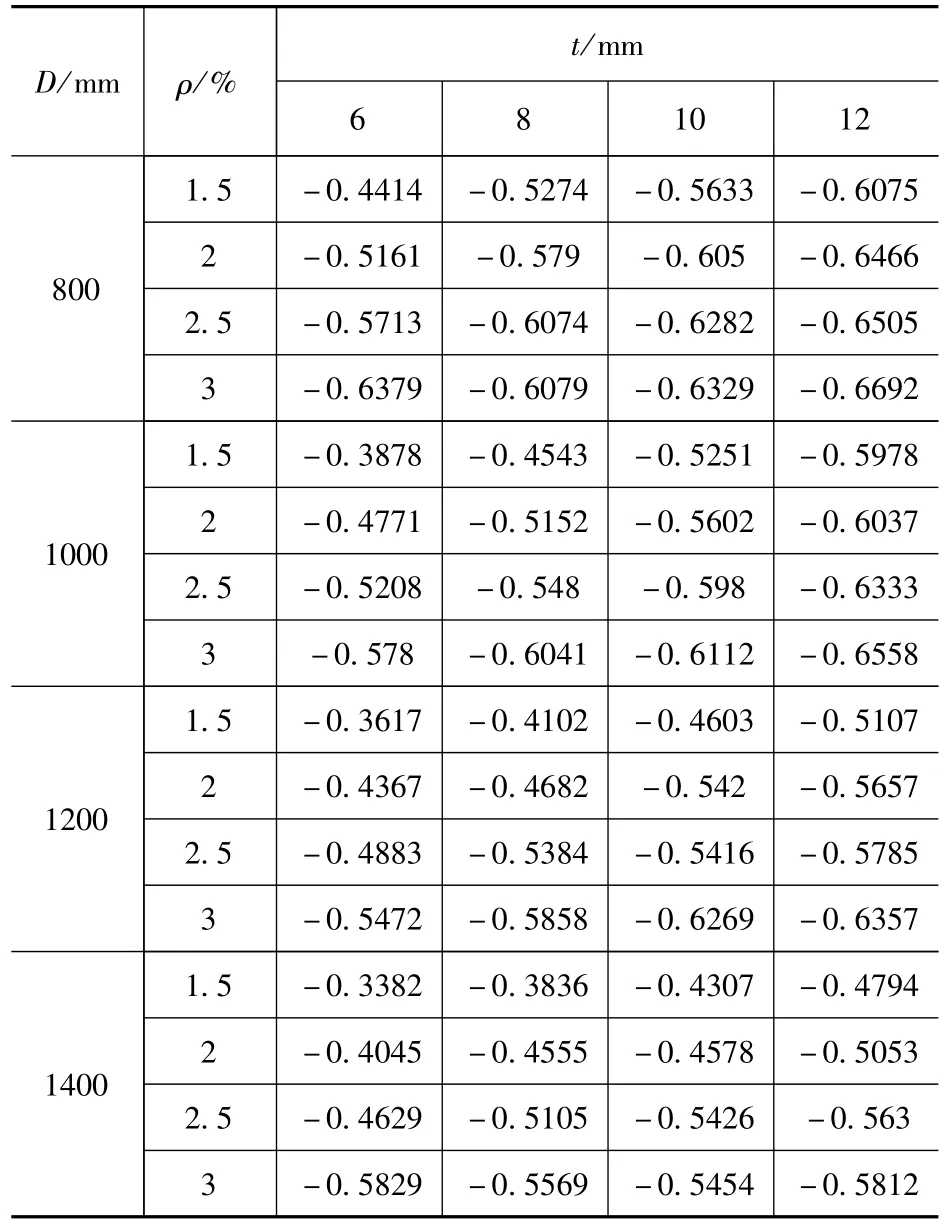
表3 不同桩身参数下a的取值Tab.3 Values of a under different pile parameters
3.2 纯弯状态下的抗弯承载力M0计算
基于程序的计算结果,表4给出了不同桩身参数下M0的取值。通过多元非线性回归分析,对M0值进行了计算公式的拟合,结果见公式(16):
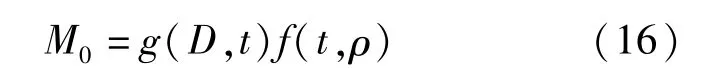
其中:
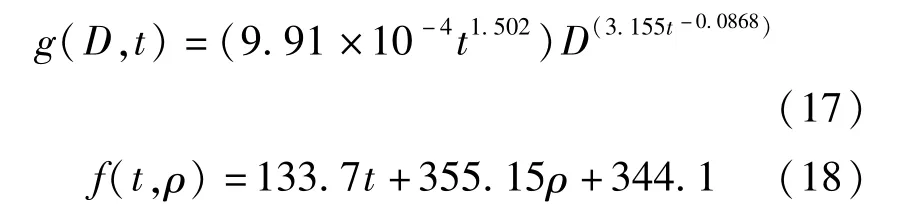
式中:D、t均以mm为单位,M0以kN·m为单位,ρ以百分数表示。
该计算公式求得M0值与理论值的相对误差均在5%以内,因此,根据该计算公式求得的结果与理论值吻合良好,可以满足工程的需要。值得一提的是,除了可以采用上述的公式求解M0值以外,在实际应用中,也可以直接根据表4利用插值法求得M0值。
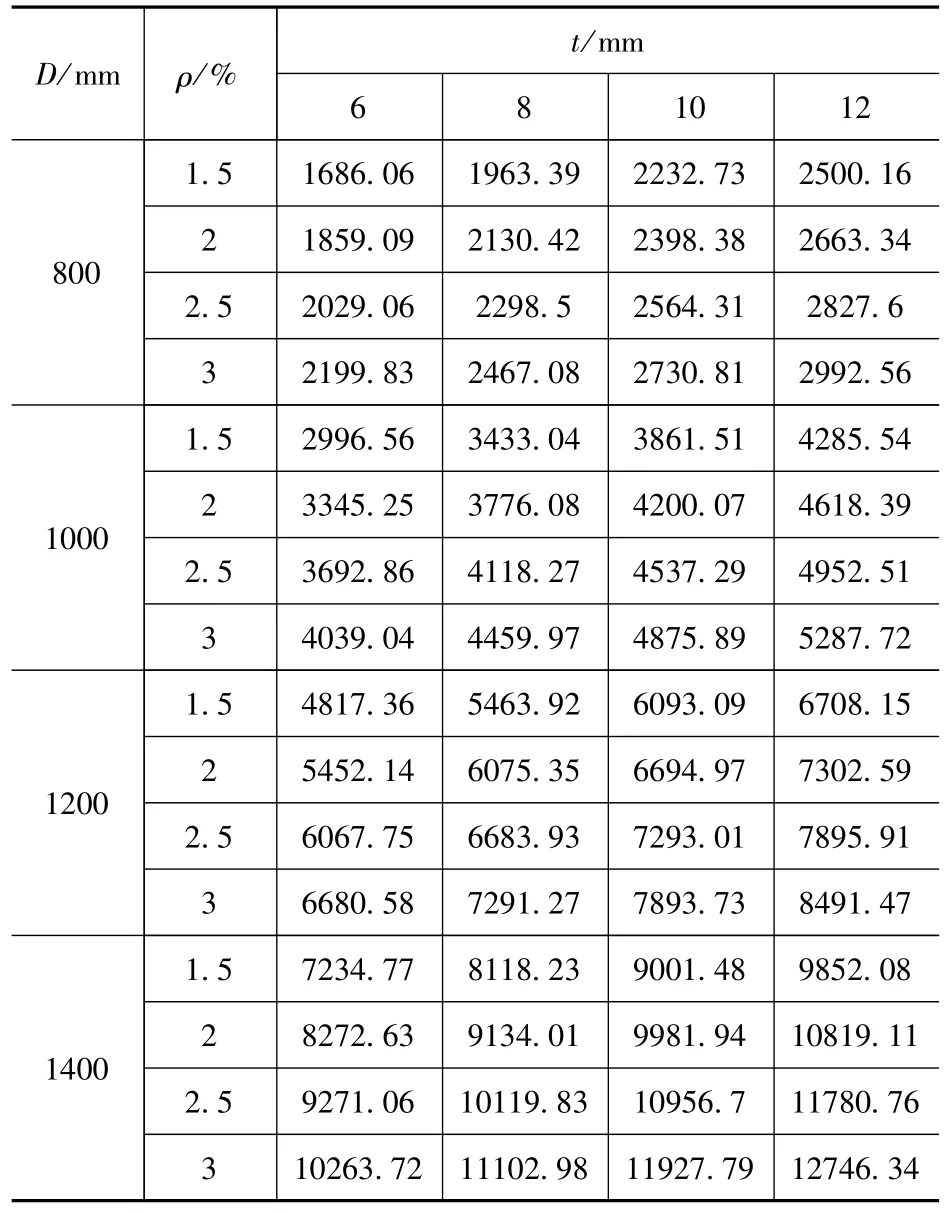
表4 不同桩身参数下M0的取值Tab.4 Value of M0under different pile-body parameters
4 结论
基于有限元理论,提出了采用有限条分法计算配筋钢管混凝土构件在拉弯复合受力状态下的极限弯矩。采用MATLAB软件编制了相应程序,研究了不同因素下M-T归一化曲线的变化规律。基于程序计算结果,主要得到以下结论:
1.截面直径、钢管厚度、配筋率、钢管及钢筋的屈服强度越大,其抗弯承载力大。
2.截面直径是影响截面抗弯承载力的主控因素。在相同的轴拉力作用下,随着截面直径的增大,其承载力呈现非线性增长,且增长速率越来越快。
3.钢管厚度、配筋率及钢管屈服强度越大,M-T归一化曲线朝偏离原点方向的鼓曲程度越大;而对于截面直径则相反,其取值越大,M-T归一化曲线朝偏离原点方向的鼓曲程度越小。
4.拟合了配筋钢管混凝土构件的M-T归一化曲线及纯弯状态的抗弯承载力M0计算公式,并给出了相关参数的取值表。在实际应用中可根据需要采用设计表法或公式法计算配筋钢管混凝土构件的抗弯承载力。

