基于非奇异终端滑模的制动缸自抗扰控制研究*

刘芳璇, 谢程程, 彭 慧, 王桂荣

(1.西安铁路职业技术学院 ,西安 710026;2.喀什师范学院 物理系, 新疆 喀什 844000;3.中国计量大学 机电工程学院，杭州 310018)

0 引言

现代电力机车基础制动装置通常采用独立的踏面制动单元,通过闸瓦与轮对踏面的直接接触(能耗制动)产生制动力迫使机车制动,并将其动能热散逸[1]。因此,应对闸瓦位置控制动态响应和精度进行合理设计,防止其响应缓慢或与踏面过分接触,从而避免制动不及时或抱死滑行现象,确保闸瓦的制动可靠性和使用寿命[2]。

实际工况中,闸瓦通过连杆机构与制动缸活塞一侧相连,活塞另一侧连通高压风源,其压力值取决于控制其流速大小的伺服阀阀芯开度,而阀芯开度由控制电压所决定,因此需通过对电压的控制保证轮瓦接触间隙在许用范围之内。文献[3-4]针对制动缸内压力的变化采用T-S模糊预测控制,但其文中在制动缸建模时均未考虑到轮对踏面受车体静压力挤压形变和通过钢轨接头、道岔和不平顺路段时所受的径向冲击形变,所用模糊规则较为复杂且压力跟踪性能并不理想。文献[5]通过动力学建模及数值仿真对踏面制动器的制动过程进行分析,但在建模及控制器设计过程中未充分考虑制动缸标称参数时变漂移及缸体内壁与活塞接触面因非严格配合导致的内部压力漏损,导致所测压力响应时间较理论值滞后。文献[6]采用经典PI预控列车管及风缸压力,通过控制减压阀阀口开度改变出口风压,但囿于系统强非线性及时变扰动,仅通过PI控制偏差的变化已无法满足精确控制时动态性能的要求。因此,欲满足更为精准的动态控制和响应时间,需充分兼顾制动缸闸瓦位置控制系统中外部负载扰动(如上述车体静压力挤压及不平顺路段的冲击)及内部参数摄动(如参数漂移及压力漏损),应进行控制器变结构设计,使控制系统的输出响应能够满足动态及稳态性能要求。

由于滑模控制器[7-8]可针对外部时变干扰、未建模动态及内部参数漂移进行设计,应用于非线性系统时具备强鲁棒性等特点,较之于PI更具优良的动态性能。为缩短滑模面的到达时间及避免终端滑模控制输出的奇异性,且抑制参数摄动及扰动的不利影响,本文针对制动缸闸瓦位置控制系统设计了一种基于非奇异终端滑模的自抗扰控制器,引入模糊补偿因子以抑制滑模面及控制器中的奇异点跳变和未建模动态并采用带加速度因子的细菌觅食算法(AF-BFA)进行控制器参数优化,使得控制系统在制动工况下的输出量快速精确跟踪给定值,并能够克服内部参数摄动和外部负载扰动的影响。

1 基于非奇异终端滑模的自抗扰控制器设计

机车制动缸等效气动伺服数学模型如下:

(1)

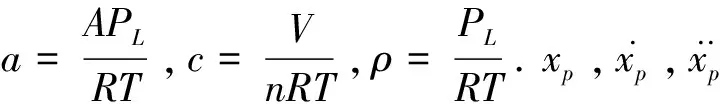
(2)

假设参考输入xd各阶导数存在,定义跟踪误差:

考虑各状态变量误差面动态,同时为缩短滑模面到达时间,设计非奇异终端滑模面为:

(3)

式中，β>0,1<γ<2,λ1,λ2>0。

定义扩张状态观测器:

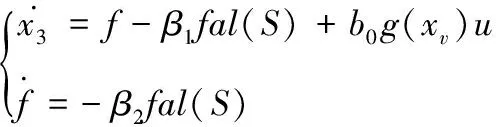
(4)

式中，f=α1x1+α2x2+α3x3+(b-b0)g(xv)u+d,

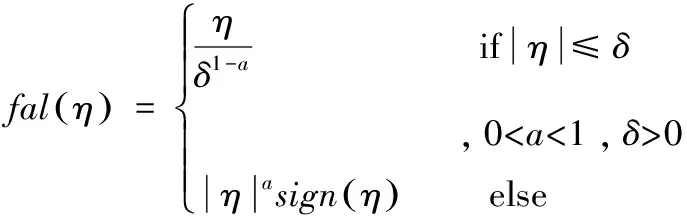
利用模糊逻辑系统[9]逼近过零摄动量,降低跳变对控制器的影响,选择模糊逻辑逼近准则为:

(5)

根据滑模面可达条件,结合Lyapunov方法,设计非奇异终端滑模控制器如下:

(6)

(7)

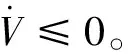
2 引入加速度因子的细菌觅食算法

本文采用引入加速度因子的细菌觅食算法(AF-BFA)对非奇异终端自抗扰控制器(NST-ADRC)参数进行优化。按照参数预选值的±10%范围内生成初始解集,采用AF-BFA进行精确求解。在小生境生态中,细菌翻转与游动(趋化)的方向与可觅食物浓度正相关。趋化的加速度因子表明该加速度方向上物质浓度的梯度变化程度,细菌在趋化过程中可根据各方向上加速度因子的差异选择最优路径快速接近食物,并按照此因子时变调节自身的移动速度。

定义加速度因子为:

(8)

引入加速度因子的概念动态调整步长,既可在算法初期步长较小时防止过早收敛而陷入局部最优解,增强算法的初始解遍历寻优范围;也可在算法后期进行精确计算时,不至因步长较大而降低算法的寻优精度[10]。同时,引入服从(μ,σ)=N(0,1)的高斯分布型随机扰动模拟小生境中的流质扰动,细菌个体受此扰动影响,概率性地跳出当前最优解,寻求觅食更优路径。

Xi′=Xi+Xi·N(0,1)

(9)

对既得最优解进行变异替换,使之在变异条件下求算对应的适应度,若替换后最优解对应的适应度较替换前大,则认为替换后的解优于替换前的解。概率替换所得解,使之跳出局部最优区间,增进算法在较大区间内搜寻最优解的能力。

由式(4)可知,扩张状态观测器参数β1、β2、b0未知。为获取满意的过渡动态特性,降低参数关联性影响,采用AFBFA算法对上述参数进行迭代寻优。以式(10)ITAE指标作为目标函数,引入控制量的平方项弱化振荡,引入输出绝对值作为惩罚项平抑超调。

(10)

式中，ey(t)=y(t)-y(t-1),y(t)为被控对象输出,tr为上升时间,w1,w2,w3,w4为各项加权值。

3 仿真结果及分析

采用经AF-BFA优化的NST-ADRC对制动缸闸瓦位置控制系统进行仿真研究。系统制动时内部风压流向如图1所示。制动管向大气排风减压,三通分配阀活塞带动滑阀左移,阻断制动缸连通大气,导通副风缸至制动缸的气路,使得制动缸活塞受压右移,推动闸瓦移向轮对。制动缸闸瓦位置控制系统参数见表1。

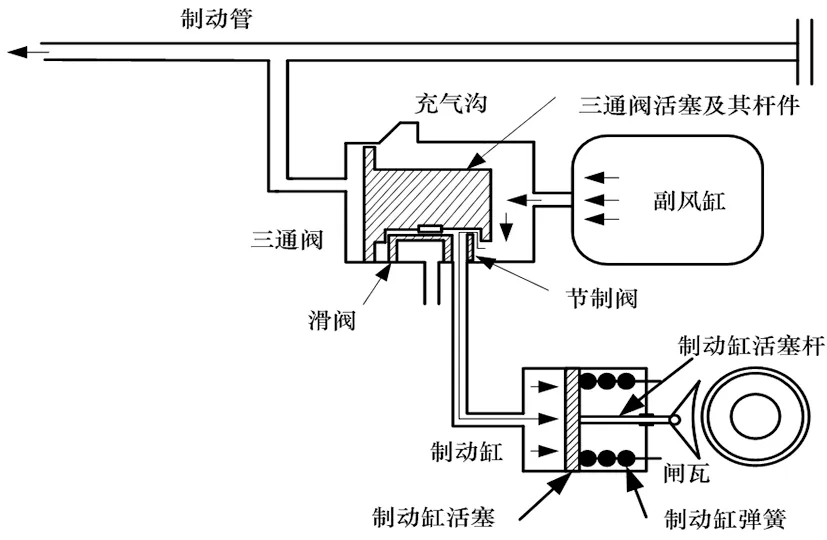
图1 制动状态时系统内部风压流向

图2为分别采用模糊PID和NST-ADRC的闸瓦位置指令跟踪曲线。考虑实际信号存在机器读取时间,并非阶跃跳变,而是以指数形式趋近收敛于稳态,即:

xcom=xs(1-e-t/tr);式中xs=1mm;tr=0.02s

定义轮瓦接触面反向时变作用力及系统内部标称参数因工作点变化而产生的摄动分别为:

M′=M+0.85Msin(πt);

选取自抗扰控制器参数优化区间如下:

采用AF-BFA对上述参数进行寻优,迭代100代后得:β1=42.2143,β2=47.8336,b0=82.2194。

图2 位置输入指令跟踪曲线

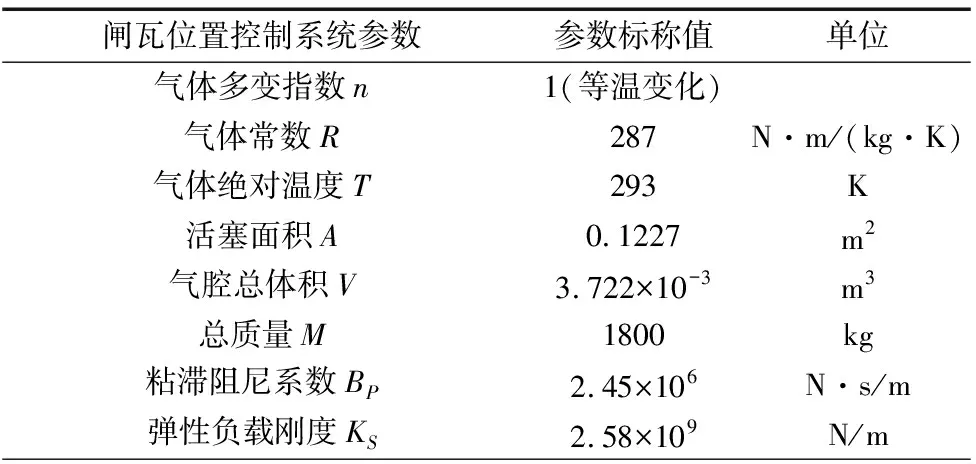
表1 制动缸闸瓦位置控制系统参数标称值

续表

由图2、图3可知,采用模糊PID的位置控制系统虽然能够根据模糊规则的变化较为有效抑制扰动影响,但上升时间内由于模糊控制规则较为固定,使输出滞后,跟踪效果不佳(上升时间长达0.2s,跟踪误差最大接近0.33mm,恢复跟踪时间接近0.2s);而基于AF-BFA的NST-ADRC针对干扰和参数时变而设计,在保证系统上升时间内对输入指令位置跟踪性能的同时,亦有效抵消参数摄动和外部较大扰动对系统的影响,形成近似无偏跟踪;而调整时间内,由于采用AF-BFA算法对控制器参数进行优化,并引入模糊补偿因子补偿ADRC的静差,可保证稳态无超调输出,误差曲线得以迅速收敛并恢复对输入量的跟踪。

图3 位置跟踪误差曲线

由图4、图5可知,相比于模糊PID依据模糊规则不断调整致使控制输入存在抖振,NST-ADRC由于引入模糊补偿因子抑制和补偿控制器过零点跳变和未建模动态,使控制输入在零点附近切换平滑无抖振,且较模糊PID控制输入曲线(用时0.12s)更为迅速终结收敛于零状态(用时0.05s)。系统在有限时间(0.02s)内到达NST滑模面,即在有限时间内实现Lyapunov一致渐近稳定,切换面抖振较小,切换过程较为平滑。综上所述,制动缸闸瓦位置控制系统具备较强鲁棒性,可有效克服外部压力扰动和内部参数摄动,对输入指令实现近似无偏跟踪。

图4 控制量输入曲线

图5 非奇异终端(NST)滑模面

4 结论

本文针对制动缸闸瓦位置控制系统中制动缸标称参数漂移和内部风源压力漏损,轮瓦接触面受车体自重挤压和不平顺路段冲击等实际工况,设计了基于非奇异终端滑模的自抗扰控制器。为抑制控制器在零点处的跳变和未建模动态响应,引入模糊补偿因子并设计了其参数自适应律;为使控制器输出动态性能最优,降低参数关联性影响,采用引入加速度因子的细菌觅食算法对控制器参数进行寻优。本文设计的控制器具有优点如下:

(1)滑模面选用非奇异终端滑模,避免了终端滑模面的奇异问题,滑模面因此实现快速收敛;

(2)控制器引入模糊补偿因子抑制过零跳变及未建模动态,有效降低控制器的输出抖振;

(3)算法优化控制器参数配比,使得系统输出更为快速精确跟踪给定输入;

(4)结合自抗扰控制算法,可有效抑制负载扰动和参数摄动对系统输出的影响。

如何将本文所阐述的理论研究成果与实际工况相结合,是下一步研究的重点。