基于决策树C4.5算法的制造过程质量管理*

周 涛，吉卫喜,b，宋承轩

(江南大学 a.机械工程学院；b.江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122)

0 引言

随着制造业的发展，企业之间的竞争愈加激烈，所以产品质量水平成了企业竞争制胜因素，所以对产品制造过程的质量严格管理成了保证产成品质量的关键过程。目前，在制造管理过程常用的质量管理方法为统计质量控制(SPC),该方法只能通过控制图反映加工过程产品质量波动情况，判断加工异常，却并不能反映出具体影响因素[1]。随着大数据的发展，产品生产过程的大量数据被保存下来，其中不乏许多生产过程不可测得却对产品质量有重要影响的工艺质量数据。如何有效利用这些数据，从历史质量数据中获得关键质量信息反馈于生产过程，改善产品质量成为近年来的研究热点，也越来越被企业决策者所关注。

本文将研究基于决策树数据挖掘方法的产品制造质量管理方法，主要的目标为充分利用生产过程质量数据，建立产品质量因素分析模型，挖掘生产过程参数对产品质量的影响，找出隐藏的生产规律，用于对生产过程的质量因素的预测，为质量改进和车间调度提供决策支持。

1 质量分析模型

采用决策树算法进行质量控制分析主要是对生产中积累的数据建立模型，能够运用模型对产品质量历史数据进行统计、挖掘，找出质量的影响因素，发现数据中潜藏的规律并反馈至生产过程，为企业持续改进质量提供决策支持[2]。

1.1 C4.5算法简述

决策树分类是数据挖掘中监督分类技术的一种，是通过一组无次序、无规则的实例中推理出决策树表现实行的分类规则，该分类方法具有较好的通用性，可理解性强，目前已经应用于很多分类问题当中，如网络流量，质量评价等[3]。C4.5算法的优点是分类准确率高、速度快，而且采用信息增益比例来选择属性，避免了ID3算法中用信息增益选择属性会出现多值偏向的问题，并能够完成对连续属性离散化的处理，以及对不完整数据进行处理[4]。

C4.5算法是数据挖掘的分类算法，因为其具有分类速度快、模型直观易于理解、适用字符型变量的优点，而且筛选不重要因素效果好，准确率较高，所以选用决策树C4.5算法作为本文制造过程质量数据挖掘处理方法。

1.2 质量决策树模型

设S是训练样本集，它包括n个类别的样本，这些类别分别用C1，C2，……Cn表示，那么S的熵(期望信息)为：

(1)

式中，Pi表示类Ci的概率。如果将S中的n类训练样本看成n种不同的信息，那么S的熵表示对每一种信息编码需要的平均比特数，|S|×E(S)就表示对S进行编码需要的比特数，其中，∣S∣表示S中的样本数目。样本的熵越大，它的概率分布越均衡，样本集的混杂程度就越高，所以熵是度量训练集的不纯度的，决策树的分支原则是使划分后的样本子集越纯越好，即熵越小越好。

设属性A将S划分为m份，根据A划分的子集的熵计算方法为：

(2)

其中，|Si|/S表示S的第i个子集占总样本的权重；信息增益用于衡量熵的期望减少值，所以，属性A对S的划分获得的信息增益为:

G(A)=E(S)-E(A)

(3)

G(A)越大，说明选择的测试属性A对分类提供的信息越多。

信息增益是一种衡量最优分支属性的有效函数，但是它倾向于选择具有大量不同取值的属性，不能保证带来良好的预测效果，因此需要新的指标来克服这种偏倚。分割信息量SI(A)可对这种偏倚进行补偿，它反映的是属性A本身的信息量，实际上它将信息增益进行了归一化，其定义为:

(4)

再由式(3)、式(4)得出增益比例GR(A)：

(5)

增益比例是信息增益与分割信息量的比值。对每个属性依次计算出信息增益和信息增益比例，然后选取信息增益比例最大的属性作为树的根节点，依次展开根属性的每一个属性取值，递归形成决策树。

1.3 决策树简化

基本的决策树构造法没有考虑噪声，因此生成的决策树完全与训练样本拟合，在有噪声的情况下，完全拟合将导致过分拟合，即分类模型对训练数据的完全拟合反而使分类模型对现实数据的分类预测性能降低[5]。为了使决策树简单直观易于理解，采用后剪枝方法处理基本决策树。剪枝是一种拟合-化简的两阶段方法，它允许决策树过度生长，再根据一定规则剪去多余的枝叶。

2 模型实验及分析

本案例的研究数据来自某电梯零部件制造公司，以齿轮加工中滚齿加工质量问题为案例进行研究。

2.1 数据准备

由于实际生产多样、复杂性，导致车间采集到的原始数据无法直接使用，为提高决策树模型的质量，需要进行数据预处理。首先利用SQL Server2008数据库将相关研究属性整理到一张可数据挖掘用的表(QDM)内，相关查询语句如下：

Insert into QDM

Select * from Documentinfo a left outer join

Transmitinfo bOn a.docid=b.docid

Where department=’质量部’

然后抽取研究对象，并对表QDM进行过滤、去噪处理。

受数据挖掘算法时间和空间复杂度的影响，从采集的滚齿加工齿轮质量历史数据中抽取相应的特征属性，获得数据样本，包括的特征属性有：批次号、生产设备、班组、操作员工号、不良现象以及不良现象影响因素。部分数据集如表1所示。为基于决策树的产品质量分析提供数据支撑。

表1 部分样本数据

2.2 决策树模型建立

用C4.5算法对抽取的数据集进行分类计算以获得决策树模型，具体计算过程如下。

训练集的目标属性为缺陷原因，属性值包括机床磨损、齿坯材质、一次切削量、滚刀的选择、滚刀安装精度以及滚刀刃磨质量。由公式(1)，计算缺陷原因的熵值E(缺陷原因)为：

E(缺陷原因)=2.639658688

该公司滚齿加工的生产设备有三个型号，分别以Z1，Z2，Z3编号。根据三种设备在样本集中的记录数，求得三种设备的权重分别为0.37、0.33、0.3。由公式(1)分别求出三种设备的信息熵：

E(Z1)=2.522443772

E(Z2)=2.594235594

E(Z3)=2.661074065

运用式(2)、式(3)可以求出生产设备的熵值和信息增益为：E(生产设备)=0.37E(Z1)+0.33E(Z2)+0.3E(Z3)=2.587724161;G(生产设备)=E(缺陷原因)-E(生产设备)=0.051934527。

同理可得其他属性的信息熵为：

E(班次)=2.587724161

E(操作员)=2.587724161

E(缺陷名称)=2.587724161

各属性的信息增益为：

G(操作员)=0.080171688

G(班次)=0.042480298

G(缺陷名称)=1.457623666

运用式(4)计算各属性分割信息量S：

SI(生产设备)=1.579641206

SI(操作员)=1.906181896

SI(班次)=0.924818705

SI(缺陷名称)=2.413194108

运用式(5)，由以上求出的信息增益和分割信息量即可求出各属性的增益比例：

GR(生产设备)=0.03287742

GR(操作员)=0.042058782

GR(班次)=0.045933649

GR(缺陷名称)=0.604022553

由上述计算结果可以看出缺陷名称属性的信息增益率明显大于其他所有的属性，所以选择缺陷名称属性作为决策树的根节点，构造决策树。

生成的完全决策树对样本分类时会产生“过度拟合”问题，因此必须对它进行化简。本文通过采用后剪枝策略，从树的叶子开始剪枝，逐步向根的方向剪，剪枝完成后，得到制造质量分类决策树，如图1所示。

图1 质量因素分析决策树

2.3 评估

为了对决策模型有效性进行检验，从数据库随机抽取200条记录来测试训练后的模型，得出的混淆矩阵为：

为了让模型有效性更直观，用决策准确率来表示模型的可正确分类概率，计算公式为：

由混淆矩阵可计算出模型的准确率如表2所示。

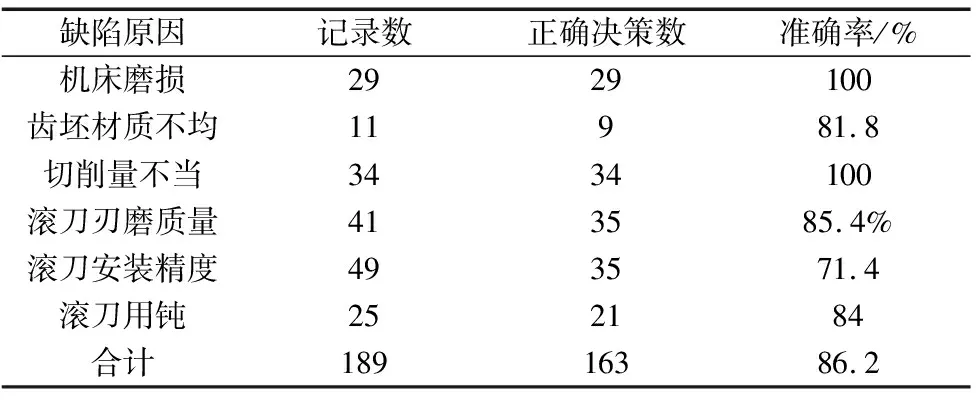
表2 缺陷原因决策准确率

从表2来看，该模型对测试集数据的质量因决策准确率达到了86.2%，从实际应用角度看，该模型方法具有良好的性能，可满足公司决策需求。

2.4 规则提取

从决策树图1可以获取如表3所示的规则。

表3 决策树提取规则

在制造过程产品缺陷形成的因素涉及多方面，表面上难以分析，而基于数据挖掘决策树提取的规则可以为质量管理和车间决策人员提供一定的质量性能控制预测和车间人员设备调度的参考依据，帮助管理人员发现产品质量问题的潜在原因，帮助企业持续改善产品质量。例如对于常见的出面出棱的质量问题，根据表中规则10～13，若是Z1号生产设备，则很大概率是滚刀刃磨不合格；若是在3号设备上生产的，主要原因是滚刀安装精度有误差；若是在Z2设备上由工号209或409员工操作，则是因为滚刀质量不达标，是员工疏于检查是否应该换刀，员工专业技能影响较小；若是员工384或237操作，则质量问题是滚刀安装精度有误差，则需要对两个操作员工进行专业技能培训来提高一次生产合格率。所以总的来说，对于出现齿面出棱质量问题，一要着眼于控制滚刀刃磨质量；二要提高操作者专业技能，保证安装滚刀时正确操作，保证各项指标；三要对Z1和Z3设备的主轴进行旋转精度复查，修复调整滚刀主轴轴承，尤其是止推垫片。对于操作员409，其在设备Z2和Z3上工作时出现质量问题次数较多，可能因为其对设备Z2、Z3熟悉度低，在以后的派工过程中，考虑将操作员409优先派到设备Z1上工作。

通过以上对模型和规则的分析讨论，验证了决策树模型不只可用于预测质量的合格与否，在寻找产品质量隐含影响因素和决策质量缺陷原因方面同样可以发挥作用，所提取的规则可作为质量管理和车间调度决策依据。同时，随着后期对该模型的进一步研究完善以及制造企业信息化智能化程度的逐步深入，可将决策结果作为知识建立质量诊断知识库，进一步研究产品质量影响因素智能诊断方法，为制造业质量管理智能化添砖加瓦。

3 结论

本文根据企业实际需求，利用车间制造过程积累的质量数据，运用决策树C4.5算法，分析了影响产品质量的主要因素，建立了基于C4.5算法的制造质量分析模型，为产品质量问题的决策诊断提供了一种可行方案，同时为企业的产品质量的持续改进和车间调度决策提供了一定程度的数据支持。经实际数据检测，该模型所达到的准确率可满足公司质量影响因素决策诊断的需求，所获得的规则对生产有一定的指导作用，证明了模型的有效性。