全矢谱在滑动轴承转子系统油膜失稳中的应用*

马凌云，陈 宏

(郑州大学 机械工程学院 振动工程研究所，郑州 450001)

0 引言

旋转机械越来越向大跨度、高转速、柔性轻结构方向发展，滑动轴承转子系统中转定子之间的油膜力与之对应的油膜失稳问题日益突出。油膜涡动和油膜振荡是转子系统运转过程中发生的一种自激振荡，是转子系统最易出现故障之一，因此，对滑动轴承转子系统进行油膜涡动、油膜振荡的研究具有深刻意义[1-2]。

基于此，陈策等[3]针对轴承产生轴颈油膜涡动现象的机理，通过公式推导进一步探讨了半速涡动的行为特征。瓮雷等[4-7]利用有限元分析软件ANSYS建立典型的具有转子陀螺效应的转子系统有限元线性分析模型，通过多次模态求解得到转子系统的坎贝尔图，从而计算出转子系统的临界转速，并且分析了转子系统在临界转速时的特性。张新勇等[8]阐述了滑动轴承油膜涡动和油膜振荡的机理并基于此提出相对应的措施，给出一种故障在线消除方法。

由于单通道分析存在信息利用不充分的问题，因此韩捷等[9]提出了对同源信号进行融合的全矢谱技术，提取信号输出的主振矢和副振矢进行同源信息融合，解决了单通道振动信号特征提取不完整的问题。在此基础上，欧阳贺龙[10]提出了基于全矢谱技术和Hilbert解调方法上的和全矢HHT时域边际谱方法，通过理论阐述和仿真验证了其有效性。

目前全矢谱技术在滑动轴承转子系统故障诊断上的应用还比较少。为研究全矢谱技术在滑动轴承转子系统故障诊断中的应用，本文在ANSYS中建立滑动轴承双盘转子-滑动轴承系统有限元模型，通过仿真数据分析与理论值相比较验证了模型的正确性，通过全矢谱技术将同源信号相融合得到转子系统油膜失稳时的全矢Hilbert解调信号，结果表明全矢Hilbert解调信号能够更好的识别滑动轴承转子系统油膜失稳的故障特征，该结论为油膜失稳故障提供了新的诊断方法，并通过实例分析证实了全矢Hilbert解调信号相对于单通道信号在滑动轴承转子系统油膜失稳故障诊断中的完整性。

1 系统故障及仿真介绍

1.1 油膜失稳

油膜失稳包括油膜涡动、油膜振荡，是由于滑动轴承油膜力所引起的自激振荡。

由于滑动轴承存在交叉刚度系数，并且滑动轴承转子系统存在由偏心质量而产生的不平衡力，因此系统存在使转子失稳的因素。在载荷一定的条件下，当转子转速不太高时，其受到一个外部干扰力的作用，轴颈仍能回到平衡位置；但当转子转速升高到一定数值后，轴颈在外部干扰力的作用下不能回到初始位置，其中心沿一近似椭圆的封闭轨迹运动，继续升高转速，运动轨迹则成为一极不规则的扩散曲线；这时即形成油膜的失稳[2]。

转子以Ω大小的角速度旋转，当Ω>B/(2m)时，系统运动不稳定，产生油膜涡动。m为转子系统质量，B=6πLη(R/C)3，其中L为轴承宽度，R为轴颈半径，η为润滑油动力黏性系数，C为轴承与轴颈间间隙。涡动角频率为：

(1)

实际中轴颈半径R与间隙C的比值非常大，因此B趋于无穷大，则式(1)也可等同于式(2)：

(2)

此为半速涡动，比较式(1)和式(2)，可得涡动频率稍小于1/2转动角频率，并由于实际中轴承两端压力油有泄漏，一般ω=(0.43～0.48)Ω。

油膜涡动产生后，随转速升高，涡动频率和半频幅值不断增加，转子振动加剧。当转速升高到2倍一阶临界转速附近时，系统产生自激振荡，此时振动非常剧烈，半频振幅超过基频振幅，伴随组合频率特征，且提高转速也无法越过，涡动频率始终等于转子固有频率，此为油膜振荡。

油膜涡动与油膜振荡特性如表1所示。

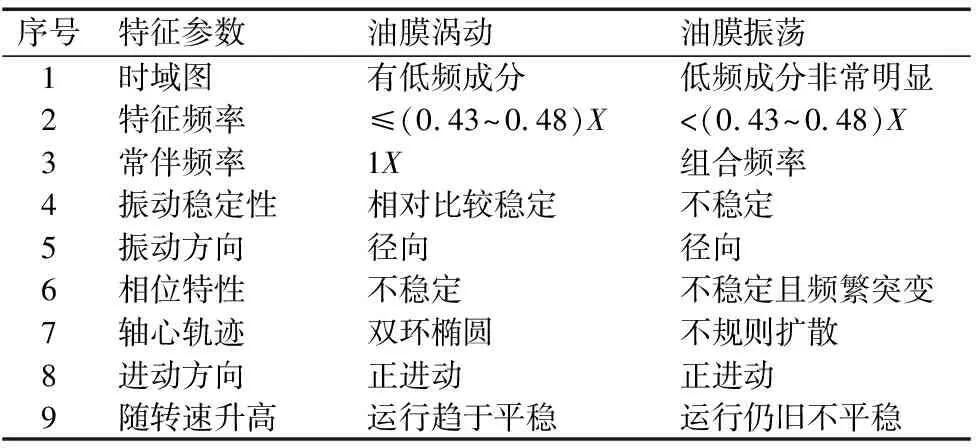
表1 油膜涡动与油膜振荡特性

1.2 基于ANSYS的转子动力学分析

有限单元法是将连续的求解区域进行离散化，将其等同于一组有限个相互连接在一起的单元的组合体，进行离散化后的模型便于计算和分析[7]。ANSYS有限元分析中，增加陀螺效应和旋转阻尼后的转子动力学方程如下：

(3)

阻尼矩阵[C]包括比例阻尼矩阵和轴承阻尼:

[C]= [C1]+[C2]

(4)

式中，[C1]—比例阻尼矩阵；[C2]—轴承阻尼矩阵。

[C1]=α[M]+β[K]

(5)

式中，

(6)

(7)

ξ1，ξ2为固有频率所对应的阻尼系数，ω1，ω2分别为转子系统第1、第2固有角频率。

2 全矢Hilbert解调技术

由于单通道分析存在信息利用不充分的问题，因此韩捷等提出了对同源信号进行融合的全矢谱技术[9]。全矢谱技术可以有效融合同源信息，更完整的反映振动特性。在实际环境中，环境噪声对于信号的分析会造成影响，而Hilbert解调技术能够解调出低频冲击所激发的高频振动频率成分然后进行低通滤波，从而减弱信号的环境噪声影响。在此基础上，欧阳贺龙等提出了一种基于全矢谱技术和Hilbert解调相结合的全矢Hilbert解调方法[10]。

(8)

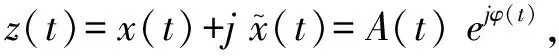
假定{xk}、{yk}为相互垂直的x，y方向上的离散序列，他们的HHT变换分别记作{xk}、{yk}，构造复序列{zk}为：

(9)

对{zk}进行HHT变换得到{zk}，经推导变换得：

(10)

式中，k=0，1，2，…，N/2-1；Zk—傅里叶变换；RLk—主振矢；RSk—副振矢；α—椭圆长半轴与x轴的夹角及振矢角；φ—轴心轨迹相位角及矢相位。

主振矢反映转子振动强度的大小，副振矢反映转子涡动的进动方向，振矢角是识别转子受力方向的重要依据。这样，通过对同源双通道的信息{xk}、{yk}进行Hilbert解调，并进行全矢同源信息融合，就能得到各个谐波下全矢谱的特征信息，减小计算量，稳健快捷。

3 系统仿真

3.1 滑动轴承转子系统仿真模型建立

根据本第1节所述，用ANSYS建立滑动轴承双盘转子系统，滑动轴承双盘转子系统模型示意图见图1，分别采用BEAM188梁单元模拟转轴， MASS21质量单元模拟刚性转盘， COMBI214弹簧单元模拟两个滑动轴承，COMBIN214单元能够模拟轴承x、y、z3个方向的油膜刚度和阻尼， 1.1节中油膜力通过设定8个动力系数实现，转子系统质量只考虑两个转盘的质量，且不考虑转轴的变形，滑动轴承转子系统参数见表2。

图1 滑动轴承双盘转子系统模型

表2 滑动轴承双盘转子系统参数

3.2 固有频率及临界转速计算

约束模型Z方向平动位移和转动位移，并约束模型X、Y方向转动位移，约束机架所有位移。考虑陀螺效应，因此设置CORIOLIS为ON。设置分析类型为模态分析，采用DAMP阻尼法，并提取16阶模态。为获取转子系统临界转速，需求出多个自转频率值所对应的进动频率值，设置转子的转速分别为0，2000，5000，8000，9000，10000，11000r/min。经模态分析后，系统坎贝尔图见图3，图中FW为正向涡动，BW为反向涡动。

图2 滑动轴承双盘转子系统坎贝尔图

我们所说的一阶、二阶临界转速往往是对于正向涡动而言，图中1X激振曲线和一阶、二阶固有频率的交点即为系统一阶、二阶临界转速，经计算，系统一阶、二阶临界转速分别为742.245rad/s和1073.4rad/s。

3.3 全矢Hilbert解调技术在油膜失稳故障中的应用

本文1.1节指出，滑动轴承转子系统在2倍一阶临界转速附近产生油膜振荡，由本文3.2节得，本文转子系统一阶临界转速为742.245rad/s，因此取系统转速为1400rad/s，采用ANSYS完全法瞬态分析，设置OMEGZ为1400rad/s，设置载荷步计算结束时间为1s，计算子步数为5120步，取0.01～0.1s的数据，即采样长度为460；相邻子步间的时间为2E-4s，即采样频率为5000Hz。此时转盘1、转盘2中心X方向、Y方向位移随时间变化的时域图和位移随频率变化的幅频图如图3a～图3d所示。

由本文第2节所述，针对全矢谱技术融合不同通道的同源信号， 取转盘1X通道与Y通道的同源信号进行融合，转盘1全矢Hilbert解调信号如图3e所示。

(a)转盘1中心位移与时间关系

(b)转盘1中心位移与频率关系

(c)转盘2中心位移与时间关系

(d)转盘2中心位移与频率关系

(e) 转盘1全矢Hilbert解调信号图3 转盘1、转盘2中心时域图与频域图

系统转速ω与频率f之间的关系如式(11)所示。

ω=2πf

(11)

当系统转速为1400rad/s时，系统基频为222.93Hz，由图3b和图3d得，此时转子系统特征频率锁定在97.83Hz即为0.44倍频频率，并存在伴随频率217.4Hz即接近基频频率，315.2Hz，326.1Hz，413Hz， 423.9Hz即其它组合频率，且97.83Hz的幅值大于其它幅值，此现象与1.1节所述油膜振荡特征现象十分吻合，验证了系统仿真模型的正确性。

然而，目前绝大多数论文只通过分析单通道信号得出结论，由图3b得，转盘1的X通道幅频信号并未显示基频信号和119.6Hz信号，且其它组合频率并不明显；由图3d得，转盘2X通道与Y通道基频信号略微有所区别且两通道0.44倍频与基频幅值大小的比较结果不相同。因此，传统上只通过单通道信号分析得出结论具有局限性。

由图3b和图3e得，经全矢融合后，全矢解调信号既反映了X通道的频率特征，也反映了Y通道的频率特征，全矢解调信号反映当发生油膜涡动时，半频信号锁定在97.83Hz与119.6Hz，并且伴随微量的3/2倍频与2倍频，经全矢融合后的信息更能体现转子系统的故障特征。由全矢Hilbert解调信号得，发生油膜振荡时的半频成分处于一定范围内而非一固定值。

4 实例分析

某厂一台20000空压机某日3级轴振动缓慢增大，3X通道值由10μm涨到17μm，3Y通道值由15μm涨到26μm，并且振动与轴承油温、油压曾相关性。经过厂内检修、压缩机厂家诊断、油检测等均未解决问题，目前通过控制油温(正常50℃左右，现在控制在40℃左右)控制振动。20000空气压缩机结构及振动测点布置示意图如图4所示。

图4 20000空压机振动测点布置图

现采用电涡流位移传感器采集20000空压机3级轴振动位移信号，采样方式为同步自由采集，采样频率为10240Hz，采样长度为4096，转轴转动速度为11929r/min。空压机3级轴转动过程中转轴位移随时间和频率变化的时域图和幅频图如图5a、图5b所示，图中X通道和Y通道为同源信号，经全矢同源信息融合后的全矢Hilbert解调信号如图5c所示。

(a) 3级轴位移与时间关系

(b) 3级轴位移与频率关系

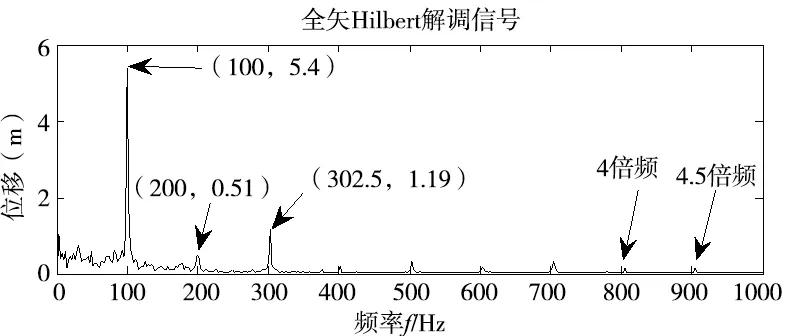
(c) 3级轴全矢Hilbert幅频图图5 3级轴振动时域图与频域图

从图5可以看出，此时3级轴振动主要是半倍频，这是典型的油膜涡动特征。此时图5a中无法看出200Hz频率即基频成分，单通道的信号存在不完整性，而由图5c得，全矢Hilbert解调信号不仅反映了X通道的幅频特性，也反映了Y通道的幅频特性；不难看出经全矢同源信息融合后，各频率成分幅值有所增加，特征更为明显，这便于实际中观测故障信号；同时，全矢Hilbert解调信号显示了单通道信号所没有的4倍频和4.5倍频，而在单通道信号中要识别出高倍频，需要更高的采样频率，而更高的采样频率提高了采样难度，在得到相同倍频的情况下，全矢谱技术降低了采样难度。

5 结论

采用ANSYS软件建立滑动轴承双盘转子-滑动轴承系统有限元模型，油膜失稳时所得单通道信号特征与理论特征十分吻合，从而验证了仿真模型的正确性。在此基础上将油膜失稳时单通道信号与全矢谱技术融合后的全矢Hilbert解调信号相比较，并通过实例分析验证，结果表明全矢Hilbert解调信号能够更好更完整地识别滑动轴承转子系统油膜失稳的故障特征，并且该方法有助于降低系统采样难度，该结论为油膜失稳故障提供了新的诊断方法。

不同于传统方法所得结果，由全矢Hilbert解调信号得，发生油膜振荡时的半频成分处于一定范围内而非一固定值。