基于改进的NSGA-II的多目标鲁棒性设备布局研究*

张萍萍，郑飂默，王诗宇

(1.中国科学院大学，北京 100039；2.中国科学院沈阳计算技术研究所 高档数控国家工程研究中心， 沈阳 110168；3.沈阳高精数控技术有限公司，沈阳 110168)

0 引言

企业在构建制造系统初期阶段，设备布局是首要解决的问题之一。研究表明，合理的设备布局至少可以节约10%～30%的物料运输费用[1]。在动态多变的市场环境下，静态布局(SFL)[2-3]方法已经无法满足生产需求。如果采用中断生产重新进行设备布局来满足生产需求，会对企业造成较大的损失。如何使布局在动态多变的需求下，表现出良好的柔性和鲁棒性，是企业能否持续发展的关键之一。

用户需求的动态性,导致传统的静态布局无法满足在连续的生产过程中后期的生产计划；同时又因为制造系统的复杂性，不可能在设备布局无法满足生产计划时，调整设备位置或重新布局。因此在制造系统设计初期提供一种布局方案，这种布局方案在动态的需求下，也能很好的满足生产任务，“不变应万变”，即鲁棒性设备布局。

1987年，Meir Rosenblatt等[4]首次将鲁棒性概念引入到制造业设备布局领域，使设备布局对动态的生产任务表现出良好的性能。鲁棒性布局是指存在一种布局方案能满足各阶段不同的生产需求，对于其中某个特定阶段，它不一定是最优方案，但对整个生产周期却是最优的布局方案。Ghorbanali Moslemipour等[5]针对鲁棒性布局问题进行了综述，详细总结了以往文献中所采用的优化模型及求解算法。刘琼等[6]则针对设施面积不等的作业车间作为研究对象，以最小化物流搬运费用和面积费用为优化目标，建立鲁棒性布局模型，并提出一种改进的蛙跳算法对其进行求解。李爱平等[7]考虑到物流搬运系统的设计对鲁棒性布局的影响，提出设备鲁棒性布局方案及物料搬运系统协同优化方法。目前鲁棒性布局的研究中采用的优化算法大都是采用加权系数将多目标单一化，但是由于加权系数的值对结果的影响较大，因此采用基于Pareto最优前沿的方法在多目标空间内直接求解，不再需要将多个目标进行单一化处理。在基于Pareto寻优的多目标优化算法[8]中，DEB在2002年提出的带精英策略的非支配排序遗传算法(Non-dominated Genetic Algorithm II,NSGA-II)是一种有效的算法，已被国内外广泛用来求解多目标优化问题。

根据上述研究现状，针对鲁棒性设备布局问题的多目标多约束的特点，以物料搬运费用、非物流关系和面积费用为优化目标建立布局模型，并利用改过的NSGA-II算法对其求得Pareto解集，用户根据实际情况择优选取布局方案。最后，通过实例验证模型和算法的有效性。

1 数学模型

1.1 问题描述

鲁棒性布局问题是连续P个生产计划期最稳定的布局方案。根据产品的工艺路线和各个子计划期设备间的物流矩阵等约束条件的变化，分析整个生产周期，引入鲁棒性指标，最后合理确定车间设备的具体位置。

以已知的n台设备为研究对象，以最小化车间物料搬运费用、非物流关系和面积费用为优化目标，建立多目标鲁棒性布局模型。

假设条件：①设备均为矩形结构，且长宽已知；② P个阶段的生产计划已定；③各产品的工艺路线已定；④同行设备的中心点位于同一条水平线上；⑤设备间的物料搬运只能走水平和垂直直线。

1.2 优化目标

以物流费用，非物流关系及面积费用作为优化目标，具体分析如下：

(1) 物流搬运费用最小化。其中：i和j表示车间设备，i,j[1,2,…,n];xi和yi为设备i的坐标值；Cij表示多设备i到设备j的单位距离物料搬运费用；fpij表示p阶段从设备i到设备j的物料搬运量。由文献[5]对鲁棒性布局问题的总结，建立车间物料搬运费用的计算公式，如式(1)，其中Dij表示设备i与设备j的距离。

(1)

(2) 非物流关系最大化。根据 LEEK等人的研究，非物流关系可表达为：

(2)

cij为设备之间的非物流密切度值，如表 1 所示，bij是布局方案中设备之间的密切度关联因子，它由资源间的实际物流距离dij和最大可能距离dmax决定，如表2所示。

表1 设备关系密切度分类

表2 密切度关联因子

非物流关系的值越大，表明非物流关系越密切，为方便利用 NSGA- II 编程解决多目标布局问题，非物流关系目标函数如式(3)所示。其中M为一个较大的常数，可根据实际情况选择。

(3)

(3) 车间面积费用最小化。采用设备自动换行的布局策略，即在同一行内的各设备长度及其设备相互间距之和超过了布局车间的长度，则该行最后一台设备自动进入下一行。

设备占地总面积简化为矩形，长度为车间总长度L，宽度为h，h可以表达为：

h=(m-1)×s+s0+0.5×wi-(s0-0.5×wj)

其中，wi为最后一行上的设备的最大宽度，wj为第一行上的设备的最大宽度，s为行间距，s0为第一行设备与车间上边界之间的最小距离，m为布局行数。不同布局方式中处于边界的设备不同，h的取值也会相应地发生变化；R为单位土地面积费用。

因此，面积费用公式如式(4)所示：

AC=min{R·L·h}

(4)

1.3 约束条件

(1) 边界约束和空间约束：式(5)保证车间设备不重叠，由于使用自动换行策略，Y方向上的行间距根据设备尺寸设定，设备之间不会出现重叠放置；式(6)保证一台设备只能被放置一次，式(7)保证在设备自动换行的布局策略下，设备不超过车间宽度；

(i,j=1,2...,n,i≠j)

(5)

(6)

h≤H

(7)

Xi和Yi表示设备i的长和宽；sij表示设备i与j的X向最小间距；L和H为车间的长和宽；hi0为设备i离车间边距界的X向和Y向最小间距；zik是0～1决策变量，其中zik=1，表示设备i在k行上，zik=0，表示设备i不在k行上，k为设备所有的行。

Rc≤δ

(8)

(9)

2 优化算法设计

为了对上述模型进行化化计算，在NSGA-II的基础上引入了DE策略[9-10]，从而使获得的Pareto最优解集保持较好的多样性，加快算法的收敛速度。

2.1 染色体编码/解码机制

染色体编码采用实数编码方式，每个染色体由两部分组成表示一种布局方案，这两部分分别为设备排列顺序和设备间净间距。

[{Mv,Mr,…,Mu,…,Mz},{Δ1,Δ2,…,Δi,…,Δn}]

其中，Δ1表示设备Mv与车间边界的最小距离，Δi表示第i台设备与第i-1台设备之间的净间距，取值范围为[Umin,Umax]。由于采用自动换行的布局策略，当第i台设备刚好是某一行的第一台设备时，Δi表示第i台设备与车间边界的最小距离。

染色体的解码即求解每台设备中心对应的坐标值，设备坐标的求解公式为：

yk=(t-1)×s+s0

(10)

(i,k=1,2,…,n;t=1,2,…m)

其中，n为设备的数量，t为该染色体对应的布局行数。

2.2 遗传算子

(1) 二元锦标赛选择算子

通过快速非支配排序以及拥挤度计算之后，种群中的每个个体都得到两个属性：非支配序rank和拥挤度nd。利用这两个属性，可以区分种群中任意两个个体的支配和非支配关系。个体优劣比较依据为：当且仅当irankjd，个体i优于个体j。

选用二元锦标赛选择算子，从种群中随机选择两个个体，根据非支配排序和拥挤度比较两个个体，选择最优的个体进入交配池。

(2) 交叉算子

对于染色体的设备排列序列部分采用映射交叉(PMX)算子。

(3) 基于差分进化的进化算子

对于设备净间距序列部分，引入DE策略进行交叉和变异，提高算法局部搜索能力，在进行精英保留策略选择子代个体时拥有较高的竞争能力，即在一定程度上保证了个体的多样性。

在DE中，常见的差分策略是随机选取两种群中两个不同的个体，将其向量差缩放后与待变异个体进行向量合成，即：

Ti=Xr1+F×[Xr2-Xr3]

其中，T为变异目标个体；F为缩放因子；Xr1表示种群中第r1个个体。F[0,1]；r1≠r2≠r3≠i。在进行变异操作时，为了保证解的有效性，要保证各“基因”满足边界条件，如果不满足边界条件，则随机重新生成。

对xi及其变异的中间体Ti进行个体间的交叉操作：

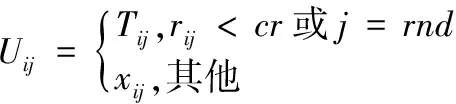
其中，Tij为变异个体Ti的第j个变量，j[1,NP]；rij为个体i第j个变量对应的均匀分布的一人随机变理，rij[0,1]；rnd为均匀分布的整数，rnd[1,NP]；cr为交叉概率，cr[0, 1]。

2.3 惩罚项

由于采用自动换行的布局策略，因此设备在X方向上不会超出工作区域。所以只需要判断在Y方向上最后一行的设备是否会超出车间区域。Pt为Y方向超出车间区域的惩罚项，如式(11)，其中m为布局行数，w最后一行设备的最大宽度，T为正的大数惩罚项。

(11)

2.4 算法流程

采用改进后的NSGA-II算法求解已建立的优化模型，DE-NSGA-II算法过程如图1所示。首先将第t代产生的新种群Qt与父代Pt合并组成Rt，种群大小为2N，然后对Rt进行非支配排序，产生一系列非支配集Zi并计算拥挤度。由于子代和父代个体都包含在Rt中，则经过非支配排序以后的非支配集Z1中包含的个体是Rt中最好的，所以先将Z1放放新的父代种群Pt+1中，依次类推，直到添加Zi时，种群的大小超出N，此时对Zi中的个体使用拥挤度比较，取前(N-num(Pt+1))个元素添加到新的父代种群Pt+1中。对新的父代种群进行选择、交叉、变异操作，产生新的子代种群。

如此反复迭代直至达到最大迭代次数，得到pareto最优解集。为了使得到的布局方案满足鲁棒性的要求，需要验证pareto解集中是否存在满足鲁棒性约束的解，若存在这样的解，则对该解进行解码，即得到鲁棒性布局方案，最后算法可能得到不只一种满足鲁棒性的布局方案，如果没有一个解满足鲁棒性要求，则重启算法。

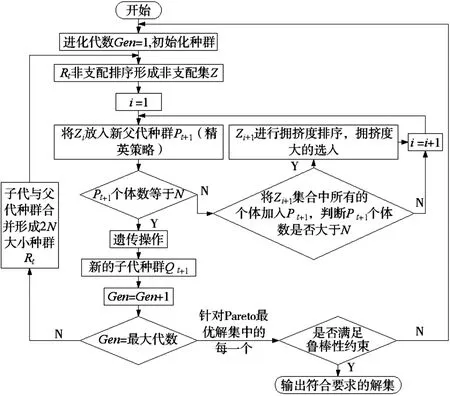
图1 NSGA-II算法流程

3 实例研究

3.1 实例描述

应用上述算法对某柔性制造单元的布局问题进行求解。该柔性制造单元的长为12m，宽为10m，需对12台设备进行布局设计，设备的具体尺寸如表3所示。设备间的净间距?的取值范围为[0, 1.5]，设备间行间距s为2m，第一行设备与车间边界距离s0为1.2m。设惩罚值T=500元，土地面积费用R=500元/m2。分析整个生产周期的实际情况以及车间安全性，可得到非物流关系cij，设备间水平最小间距要求hij和设备与车间边界的最小距离要求hi0；鲁棒性指标δ=0.07。

分析该制造单元连续3个计划期的工艺路线(表4)和物流信息(表5)，求解每个阶段的物流搬运频率矩阵。

表3 设备尺寸(m×m)

表4 工艺路线

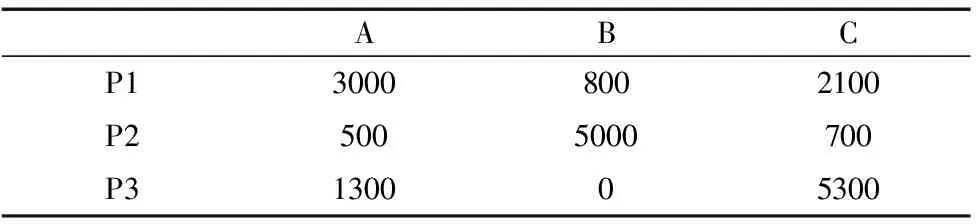
表5 生产计划

3.2 算法参数设计与问题求解

DE-NSGA-II算法的相关参数设置如下：种群规模pop=100；最大遗传代数maxgen=100；交叉概率pc=0.7，以式(1)～式(3)为目标函数，运行程序，最终得到的Pareto解集如图2所示。针对提出的鲁棒性布局模型分别应用DE-NSGA-II、NSGA-II，SADE对该鲁棒性布局模型进行多次求解，结果对比，与NSGA-II及SADE相比，DE-NSGA-II的收敛性和多样性更好，对比结果见表6。

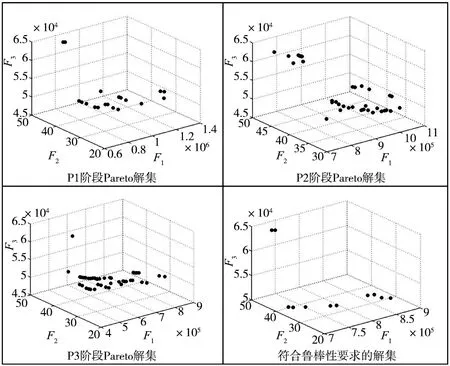
图2 pareto解集

在最终的Pareto解集中，剔除相似度比较高的布局方案，得到如表7所示的5种布局方案。方案1的目标1值是所有解集中最小的，但是目标2和目标3的值是最大的；方案5的目标3的值是最小的，但是目标1的值是最大的；方案4的目标2的值是所有解集中最小的，但是目标1和目标3的值均不是最小的。通过多次实验分析可得，不存在某种方案可以使得3个目标都达到最优。

该实例三个目标的最优解分别为F1=729698.92，F2=33.8，F3=50040，不存在任何一个个体能使三个目标值同时达到最优。企业决策者可以根据实际情况，在多种方案中选择最合适的布局方案。

表6 三种优化算法性能对比

表7 部分Pareto解集

4 结束语

针对提出的鲁棒性布局模型，利用基于差分进化与NSGA-II的多目标算法验证了该模型的有效性，克服了使用加权系数将多目标单一化求解多目标问题的缺点，可以有效地应对复杂多变的市场需求。算法设计的过程中，在NSGA-II算法的基础上引入DE策略，有效地提高了Pareto解集的多样性和算法的收敛速度，最终得出符合鲁棒性要求的布局方案集。