求解圆锥曲线离心率范围问题的常见策略

■河南省濮阳市第一高级中学

离心率是圆锥曲线的一个重要性质,是刻画圆锥曲线形态特征的基本量,因此,求圆锥曲线离心率的取值范围问题是历年高考和模拟考试的热点问题之一。解决此类问题的基本思路是构造关于a,c,e的不等式。下面结合高考题,介绍求圆锥曲线的离心率的几种常用方法,以便同学们能更好地理解和掌握此类题的技巧和规律,提高大家分析问题和解决问题的能力。

一、直接利用条件寻找a,c的关系求解

小结:通过对题目已知条件的分析,尽可能直接建立离心率的不等关系来求解。

解析:设直线l的方程为y=k(x-c)。

令x=0,得y=-ck,即点M的坐标为(0,-ck)。

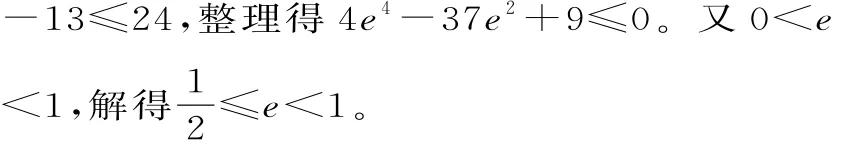
小结:解答本题的关键是如何建立k与e之间的关系,然后再利用k的取值范围来求解e的取值范围,同时要注意椭圆离心率e隐含的范围为e∈(0,1)。

二、利用圆锥曲线的第一定义或第二定义求解

小结:圆锥曲线上的点到焦点的距离或到准线的距离,通常要用它们的第一定义或第二定义来建立联系。

三、利用圆锥曲线的范围(或焦半径的有界性)求解

四、利用数形结合求解

解析:要使椭圆与圆有四个不同的交点,只需满足b＜+c＜a。

小结:将数用形来体现,直接得到a,b,c的关系,这无疑是解决数学问题较好的一种方法,也是重要的解题途径。

从以上四种求圆锥曲线离心率范围的策略来看,我们要明确求离心率范围的关键是建立a,b,c的不等关系,然后利用椭圆与双曲线中a2,b2,c2的默认关系以及离心率的限制范围,最终求出离心率的范围。