为数学点赞——名师例析数学文化(10)解析几何

■北京市第十二中学高中部

■北京市教育学院丰台分院 张 琦

本刊特邀栏目专家简介:

高慧明首届全国十佳班主任,全国著名数学特级教师,国家教育部课程改革“全国先进工作者”,全国著名高考数学命题与考试研究专家,国家教育部“国培计划”全国中小学教师培训、班主任培训、校长培训特邀主讲专家,受邀在全国各地做有关高考科学备考、班级管理等多场专题报告。现任教于北京市第十二中学高中部。

数学是一种文化的观点,早已为人们所接受。从历史上看,古希腊和文艺复兴时期的文化名人,往往本身就是数学家。著名的代表人物如毕达哥拉斯、柏拉图、泰勒斯和达·芬奇等。近代的爱因斯坦、希尔伯特、罗素等文化名人也都是20世纪数学文明的缔造者。

中国科学院院士、北京师范大学数学学院王梓坤教授曾指出:“数学文化具有比数学知识体系更为丰富和深邃的文化内涵,数学文化是对数学知识、技能、能力和素养等概念的高度概括。”在2003年颁布的《高中数学课程标准(实验)》中,更是把“体现数学的文化价值”作为高中数学课程的十项基本理念之一,给予了特别的重视。而在新修订的《普通高中数学课程标准(2017年版)》中,也在基本理念里“强调数学与生活以及其他学科的联系……注重数学文化的渗透”,要“不断引导学生感悟数学的科学价值、应用价值、文化价值和审美价值”。

为什么要这样做呢?一个重要的原因是,20世纪初期的数学曾经存在着脱离社会文化的孤立主义倾向,并一直影响到今天的数学教育。孤立主义的数学,一方面拒人于千里之外,使人望数学而生畏;另一方面,又孤芳自赏,自言自语,令人把数学家当成“怪人”。在孤立主义盛行的年代,人们普遍认为数学只是少数天才脑子里想象出来的“自由创造物”,数学是数学家的游戏。如此这般,对数学教育产生的一个严重后果就是“数学教育的传统地位陷入严重的危机。数学教学有时变成了一种空洞的解题训练”。于是,西方的数学界就有了“经验主义的复兴”。怀特的数学文化论力图把数学回归到文化层面。克莱因的《古今数学思想》、《西方文化中的数学》、《数学:确定性的丧失》相继问世,力图营造数学文化的人文色彩。

在我国,2002年北京国际数学家大会期间,“中国少年数学论坛”会场的大幅标语中,就使用了“数学文化”一词。2003年“数学文化”一词在官方文件(《普通高中数学课程标准(实验)》)中被正式使用,之后被越来越广泛地使用到大学生活动、数学教学与研究等领域。各种版本的高中数学教材基本都安排了蕴含丰富数学文化价值的“阅读材料”。更进一步,无论各省市自主命题的高考数学试卷,还是新课标全国高考数学试卷,均出现了以数学文化为背景的试题,成为新课改理念下高考改革和发展的一道靓丽风景。

在这个栏目里,我们通过系列文章对近些年高考数学文化试题或自编试题进行了剖析,为广大中学生更好地理解数学概念本真提升数学核心素养提供参考。本期我们主要谈谈解析几何试题中的数学文化。

一、阿波罗尼斯圆

阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,描述如下:

到两定点距离之比等于已知数的动点轨迹为直线或圆。

图1

如图1,点A,B为两定点,动点P满足PA=λPB,当λ=1时,动点P的轨迹为直线;当λ≠1时,动点P的轨迹为圆,后世称之为阿波罗尼斯圆。

证明:设AB=2m(m＞0),PA=λPB。以AB中点为原点,以直线AB为x轴建立平面直角坐标系,则A(-m,0),B(m,0)。

又设P(x,y),则由PA=λPB 得

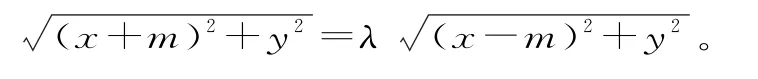
两边平方并化简整理得(λ2-1)x2-2m(λ2+1)x+(λ2-1)y2=m2(1-λ2)。

当λ=1时,x=0,轨迹为线段AB的垂直平分线。

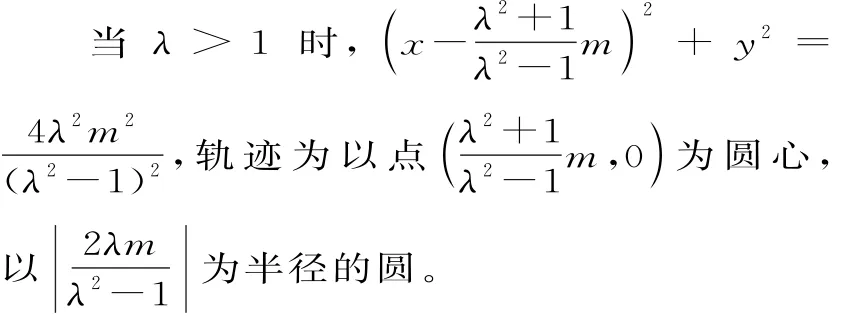
与阿波罗尼斯圆有关的试题在高考中也屡见不鲜,请看下面试题:

例1(2008年江苏13)若AB=2,AC=BC,则S△ABC的最大值为 。

解析:本题可以用边长为自变量,也可以用角为自变量,再利用二次函数或者三角函数的有界性求解,运算量比较大。如果应用“阿波罗尼斯圆”,将问题解析化,运算过程要简单许多。解法如下:

以AB中点为原点,AB所在直线为x轴建立平面直角坐标系,则A(-1,0),B(1,0),设C(x,y),由AC=BC 得平方化简整理得y2=-x2+6x-1=-(x-3)2+8≤8,所以 y ≤2×2·y≤2,所以S△ABC的最大值是2。

练习:(2014年湖北文17)已知圆O:x2+y2=1和点A(-2,0),若定点B(b,0)(b≠-2)和常数λ满足:对圆O上任意一点M,都有|MB|=λ|MA|,则:

③若点P在曲线C上,则△F1PF2的面积不大于a2。

其中正确命题的序号为 。

二、卡西尼卵形线

乔凡尼·多美尼科·卡西尼是一位意大利出生的天文学家和水利工程师,他是第一个发现土星的四个卫星的人。1675年,他发现土星光环中间有条暗缝,这就是后来以他的名字命名的卡西尼环缝。他猜测,光环是由无数个小颗粒构成,两个多世纪后的分光观测证实了他的猜测。为了纪念卡西尼对土星研究的贡献,当代人类探测土星的探测器“卡西尼号”即以他的名字命名。卡西尼卵形线是1675年他在研究土星及其卫星的运行规律时发现的。

例2(2011年北京理14)曲线C是平面内与两个定点F1(-1,0)和F2(1,0)的距离的积等于常数a2(a＞1)的点的轨迹。给出下列三个结论:

①曲线C过坐标原点;

②曲线C关于坐标原点对称;

解析:设P(x,y)为曲线C上任意一点。

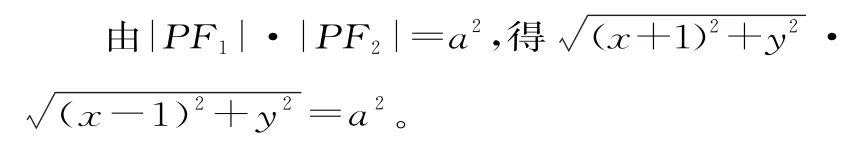
把(0,0)代入方程可得1=a,与a＞1矛盾,故①不正确。

当M(x,y)在曲线C上时,点M关于原点的对称点M′(-x,-y)也满足方程,故曲线C关于原点对称,故②正确。

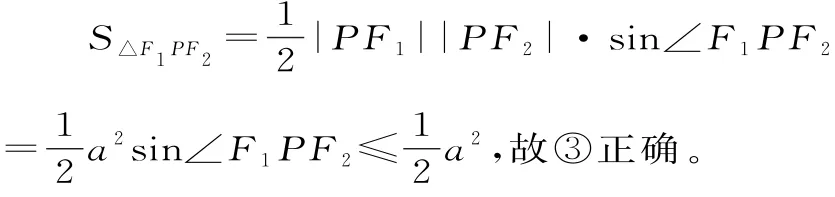
事实上,关于卡西尼卵形线我们可以展开进一步的思考:

思考1:若将“两定点”之一变为“定直线”,那么距离之比为定值的动点轨迹是什么?

思考2:若将“两定点”之一变为“定直线”,那么距离之和为定值的动点轨迹是什么?

思考3:到定点的距离与到定直线的距离的k倍之和为定值的定点轨迹是什么?

思考4:到定点的距离与到定直线的距离之差(的绝对值)为定值的定点轨迹是什么?

思考5:到定点的距离与到定直线的距离之积为定值的定点轨迹是什么?

三、椭圆规

在解析几何教学过程中,为了突出椭圆、双曲线的生成过程,老师基本都采用机械方法作图以加深同学们印象。这时往往就需要用图钉、细绳、拉链等实物辅助教学。老师和同学们其实这时候难免会有疑问,究竟有没有如同圆规、直尺一样的工具,让我们轻松地画出椭圆、双曲线呢?答案是肯定的。荷兰数学家舒腾就曾经设计了三种机械椭圆规,而其中的一种椭圆规刚好是2015年湖北高考数学试题的原型,所以我们不妨来看看这道高考试题。

例3(2015年湖北文22)一种画椭圆的工具如图2所示。O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3。当栓子D在滑槽AB内做往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C。以O为原点,AB所在的直线为x轴建立如图3所示的平面直角坐标系。

(Ⅰ)求椭圆C的方程;

(Ⅱ)略。

图2

图3

分析:(Ⅰ)因为|OM|≤|MN|+|NO|=3+1=4,当M,N在x轴上时,等号成立;同理|OM|≥|MN|-|NO|=3-1=2,当D,O重合,即MN⊥x轴时,等号成立。所以椭圆C的中心为原点O,长半轴长为4,短半轴长为2,其方程为=1。

(Ⅱ)略。

从轨迹的角度看,本题中,D,N带动点M运动,由于点N的轨迹已经知道是单位圆,所以点M的轨迹其实是单位圆的“伴生曲线”,所以我们可以采取相关点法解决该题。本题中如果设M(x,y),并记N(x0,y0),则 D(2x0,0),根 据也可得结果。

本题解题思路非常清晰、简单。这也是舒腾椭圆规的制作原理。舒腾制作了三种椭圆规,还制作了双曲线规、抛物线规。感兴趣的同学可查阅相关资料了解学习,并请思考其作图原理。

事实上,在解析几何中存在着大量的数学文化的案例,圆锥曲线在生活中也是随处可见,如椭圆形镜子、双曲线形通风塔、抛物线拱桥等。再比如在圆锥曲线发展历史过程中具有重要历史地位的dandelion球、圆锥曲线的光学性质、圆锥曲线与三角函数的奇妙联系(如图4,圆柱的截面为一椭圆时,将圆柱侧面沿椭圆的最高点所在母线展开后,椭圆则成了正弦曲线)等。

图4

另外,关于数学文化的学习,有一个误区:许多同学直觉上认为,数学文化就等价于数学史。确实,宏观地观察数学,从历史上考察数学的发展,是揭示数学文化层面的重要途径。但是,除这种宏观的历史考察之外,还应该有微观的一面,即从具体的数学概念、数学方法、数学思想中揭示数学的文化底蕴。同学们在学习过程中,既要多多关注教材内容的编排和编写意图,也要设法多途径、多侧面地理解和体会数学文化。