电动沙发机械结构的运动仿真及优化*

谢 重，谢 巍，杨 杰

(台州职业技术学院，浙江 台州 318000)

0 引 言

功能沙发近年来在中国沙发市场发展迅速，城市中等收入水平者在家具购买时，会更多地选择舒适度好的功能沙发[1]。作为休闲时首选的沙发座具，如果设计不合理，不仅起不到放松、缓解疲劳的效果，还将导致腰肌劳损、累积性创伤疾患等多种疾病[2-3]。

国内外许多学者针对不同的功能座椅进行过力学性能分析、运动功能分析及其结构参数优化等方面的研究。其中：谢巍[4]应用ADAMS对VR动感椅的结构进行了动力学仿真，分析了其运动过程中电动缸所受的扭矩；蔡欢[5]使用ADAMS软件对多功能办公休闲椅进行了运动分析，使用ANSYS软件对座椅进行了强度与疲劳实验分析；谢巍[6]使用ADAMS对办公椅联动机构进行了参数化建模，对连杆参数进行优化设计，实现了办公椅靠背在联动过程中的‘零搓背’；LI Rui-qin[7]对双自由度七杆机构进行工作空间分析，将其拆分为铰链五杆机构和RPP型二级阿苏尔杆组形式，分析了两者耦合点的工作空间和输出曲线间的特性关系，通过控制改变结构参数来达到给定的输出；刘波[8]对混合驱动的九连杆压力机进行了机构构型综合分析，利用复数矢量法建立了机构的运动学模型，并导出了九杆机构的动力学模型。

本文将针对一款多功能电动沙发，在ADAMS中进行机械装置的运动仿真分析，初步验证整体机械装置的运动参数正确性；运用平面杆系运动学理论，建立电动沙发的平面连杆系机构的运动理论模型，求解出搁脚板的角速度和质心运动速度曲线，以此验证ADAMS运动仿真的正确性；采用Matlab中的fmincon优化工具箱对目标函数进行优化求解，优化平面连杆系的参数。

1 电动沙发机械结构

电动沙发分坐姿、休闲姿和躺姿3种状态模式，由于电动沙发的机械结构模型是对称的，笔者采用其一半机械结构的机构简图。

电动沙发的3种姿态的模型如图1所示。

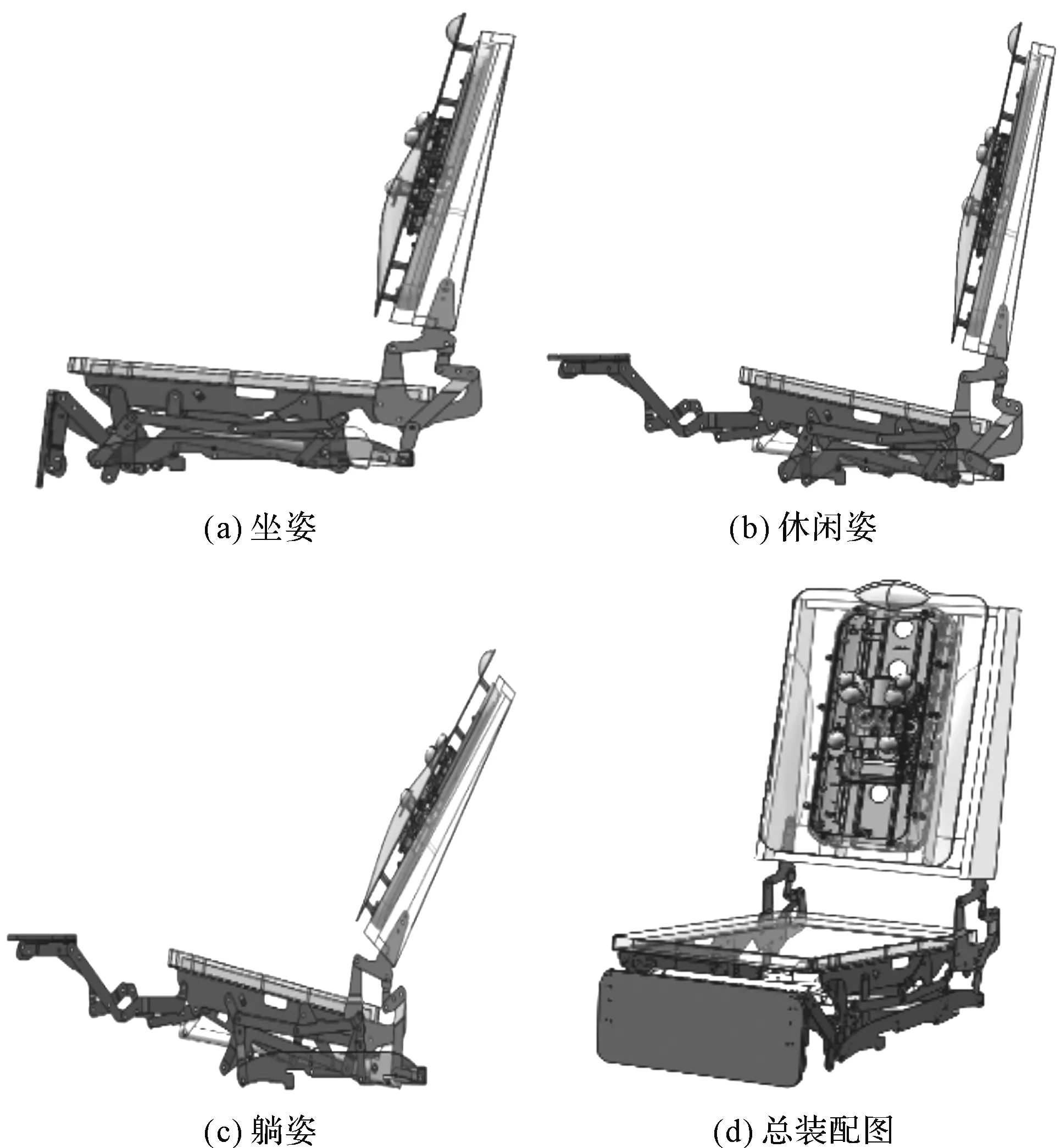
图1 电动沙发整机三维模型

电动沙发机械装置的姿态变化过程分析，如图2所示。

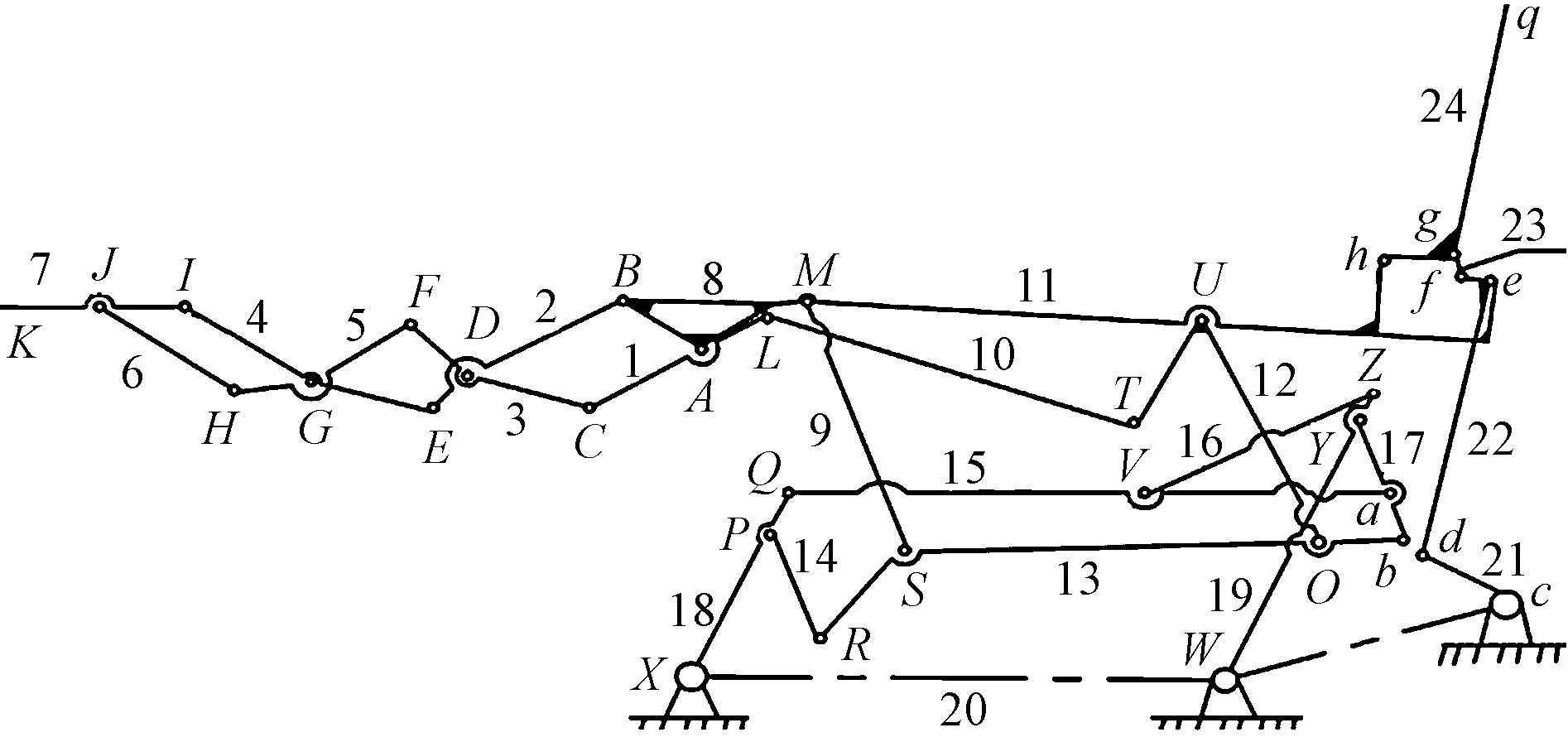
图2 电动沙发装置机构简图1，10—连接杆；2，6—搁脚杆机构；7—搁脚板；9，12，13—休闲姿四边形机构杆；11—座板；14，19—躺姿四边形机构杆；20—机架；21，23—靠背机构杆；24—靠背板

在坐姿到休闲姿的变换过程中实现搁脚板的伸展和坐板的前移，即在电动推杆12的作用下，带动连接杆10来驱动连接杆1，从而使搁脚杆机构运动实现搁脚板7伸展，同时在电动推杆12的驱动下使得与座板11连接的四边形机构MSOU运动，从而实现座板11前移。休闲姿到躺姿的变换过程中实现靠背后仰，即在休闲姿的基础上电动推杆12继续驱动，带动四边形机构QXWZ运动，从而使座板11与搁脚机构做整体的迁移，最终由座板11的前移使得靠背板24后仰。

2 电动沙发的运动仿真分析及理论分析

2.1 仿真模型的建立

电动沙发装置的机械结构为对称的平面杆系机构，本研究对其机械结构取1/2模型进行分析。将简化后模型导入ADAMS，添加材料属性，设置好单位及重力加速度。同时，为描述构件间的相对运动，需要根据实际情况对电动沙发在仿真时添加相应的转动副、移动副和固定约束。

电动沙发驱动件为电动推杆，其启停时间极短，运动平稳。笔者选定电动推杆的运行速度为22 mm/s，电动推杆的加减速时间一般为0.5 s[9]。中间时段电动推杆保持匀速运动。电动沙发运动的两个阶段如表1所示。

表1 仿真运动阶段分析

参照QB/T 4191—2011测试加载要求，可知测试加载的形式，其中，F2为77 kg，F3为24.5 kg，由于是对称模型，加载数值是实际模型中的一半。

测试加载示意图如图3所示。

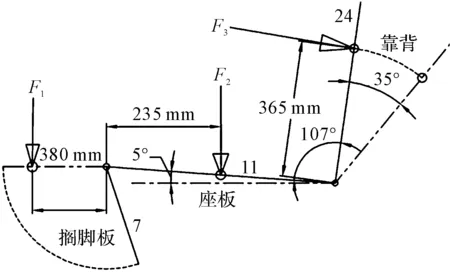
图3 测试加载示意图

2.2 仿真结果及分析

电动沙发在位姿变化的运动过程中，主要研究搁脚板、座板和靠背板的平稳性问题。本研究在ADAMS软件中进行机构的运动仿真后，提取出搁脚板、靠背板和座板的角速度和速度参数，如图(4,5)所示。

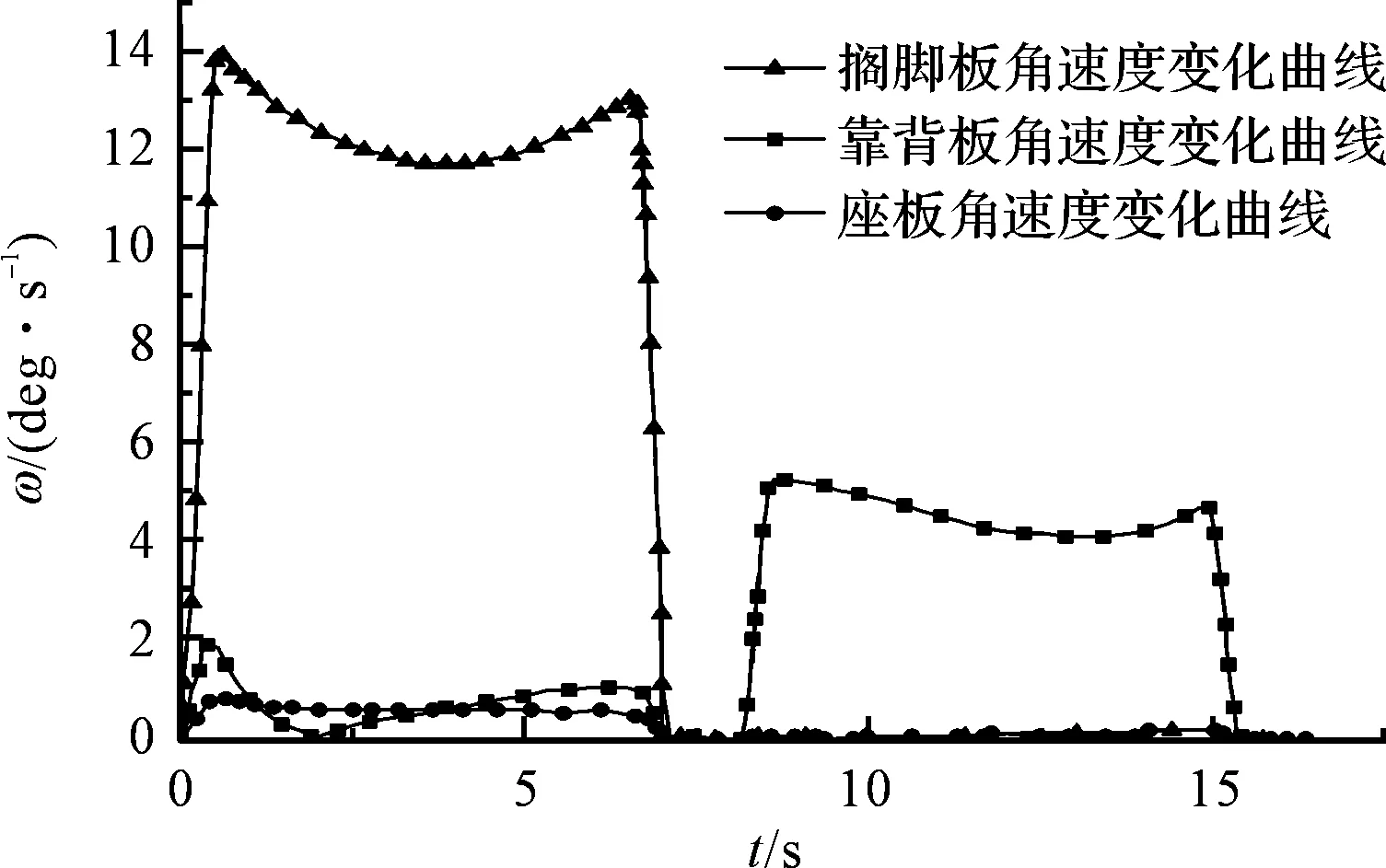
图4 搁脚板、座板及靠背板角速度曲线

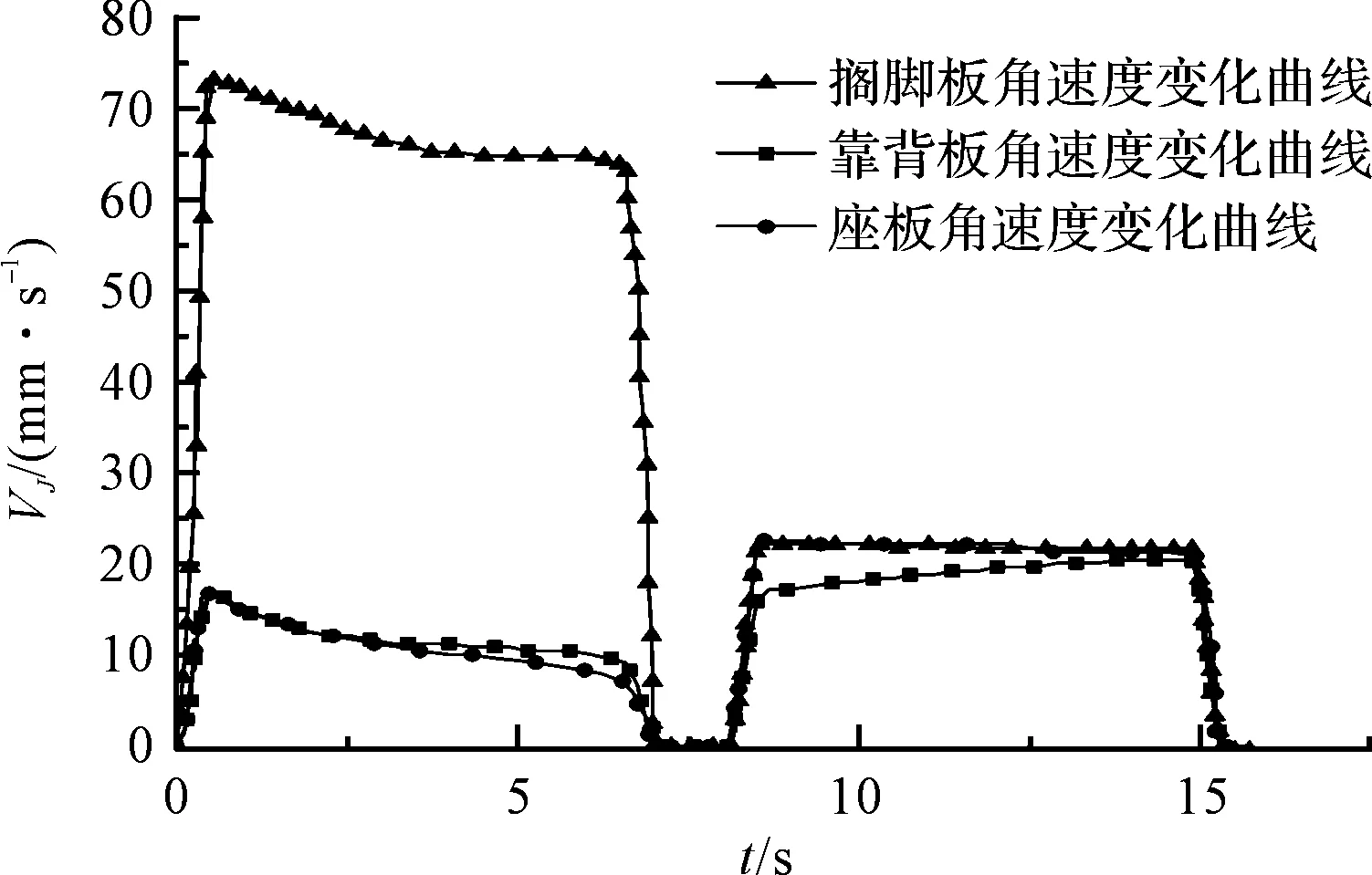
图5 搁脚板、座板及靠背板质心速度曲线

搁脚板从坐姿到休闲姿的过程中，角速度的变化最大，其变动幅度为3.5 deg/s；靠背板在休闲姿到躺姿的过程中，角速度变化值为1.5 deg/s；座板在整个运动过程中的角速度比较平稳。搁脚板从坐姿变换到休闲姿的过程中，搁脚板质心速度的变化最大，其变动幅度为11 deg/s。

在位姿变化过程中，搁脚板的速度和角速度变化幅度较大，特别是在坐姿向休闲姿转换的过程中，如表2所示。

表2 电动沙发重要部件运动参数的变动幅度

搁脚板的运动参数的变化对整个机构的运动平稳性和电动沙发的舒适性影响重大，因此需要对角速度和质心速度变动幅度较大的搁脚板部件进行结构参数优化。

2.3 休闲姿实现的运动分析及求解

由上述仿真可知：搁脚机构在由坐姿向休闲姿变化的过程中不平稳性严重，为了验证仿真的正确性，本研究对简化后的休闲姿机构进行理论分析及求解。通过去除在坐姿向休闲姿变化的过程中不参与运动的杆件和靠背模块得到机构简图，如图6所示。

图6 简化后的休闲姿机构简图

其中杆件参数含义如表3所示。

表3 简化后的机构简图中的杆件参数含义

以O为原点建立坐xoy标系，作封闭矢量多边形，建立矢量方程。该机构独立封闭环的个数为[10]：

l=P-N+1=5

(1)

式中：l—独立封闭形个数；P—机构的运动副个数；N—机构的构件总数。

各个封闭环的环矢量方程为：

l12cosθ12+l11cosθ11=l13cosθ13+l9cosθ9

(2)

l12sinθ12+l11sinθ11=l13sinθ13+l9sinθ9

(3)

r12sin(π+θ12-β12)+l10sinθ10+
l1sinθ1=lAUsin(θ11+∠MUA)

(4)

r12cos(π+θ12-β12)+l10cosθ10+
l1cosθ1=lAUcos(θ11+∠MUA)

(5)

r1cos(θ1+β1)+l3cosθ3=l8cos(β8+
∠BAM+θ11-2π)+l2cosθ2

(6)

r1sin(θ1+β1)+l3sinθ3=l8sin(β8+
∠BAM+θ11-2π)+l2sinθ2

(7)

r2cos(θ2+β2)+l4cosθ4=l5cosθ5+r3cos(θ3-β3)

(8)

r2sin(θ2+β2)+l4sinθ4=l5sinθ5+r3sin(θ3-β3)

(9)

r4cos(θ4-β4)+l7cosθ7=r5cos(θ5-β5)+l6cosθ6

(10)

r4sin(θ4-β4)+l7sinθ7=r5sin(θ5-β5)+l6sinθ6

(11)

Jv=b

(12)

其中：

于是有：

(13)

由此可求得各杆的角速度表达式。因为机构的各杆长参数已知，当各杆件相应的位置角参数θ2、θ3、θ4、θ5、θ6、θ7求解后，那么各杆件在运动过程中的位置参数也就相应的得到了求解。由图6可知，通过解析法可求得搁脚板的质心在X和Y方向运动的表达式：

X7=-[l12cosθ12+r12cos(π+θ12-β12)+l10cosθ10+
r1cos(θ1+β1)+l1cosθ1+r3cos(θ3-β3)+l3cosθ3+
l5cosθ5+r5cos(θ5-β5)+l6cosθ6]

(14)

Y7=l12sinθ12+r12sin(π+θ12-β12)+l10sinθ10+
r1sin(θ1+β1)+l1sinθ1+r3sin(θ3-β3)+l3sinθ3+
l5sinθ5+r5sin(θ5-β5)+l6sinθ6

(15)

结合式(14，15)，可求得搁脚板质心速度v7为：

(16)

由此求得了搁脚板角速度ω7和搁脚板质心速度v7关于时间的理论方程。电动沙发结构参数的初始值数据如表4所示。

本研究将其输入到Matlab中，画出相应曲线图，进一步地与ADAMS输出的搁脚板参数运动曲线进行对比分析，如图7所示。

在搁脚板角速度和质心速度曲线的仿真值与理论值的比较过程中，搁脚机构在由坐姿向休闲姿变化时，ADAMS仿真中得出的搁脚板角速度和质心速度都与Matlab计算出的理论值曲线基本相吻合，误差在5%内。因此，本研究通过对平面连杆机构的运动参数进行计算求解，验证了ADAMS仿真中搁脚板运动的正确性。

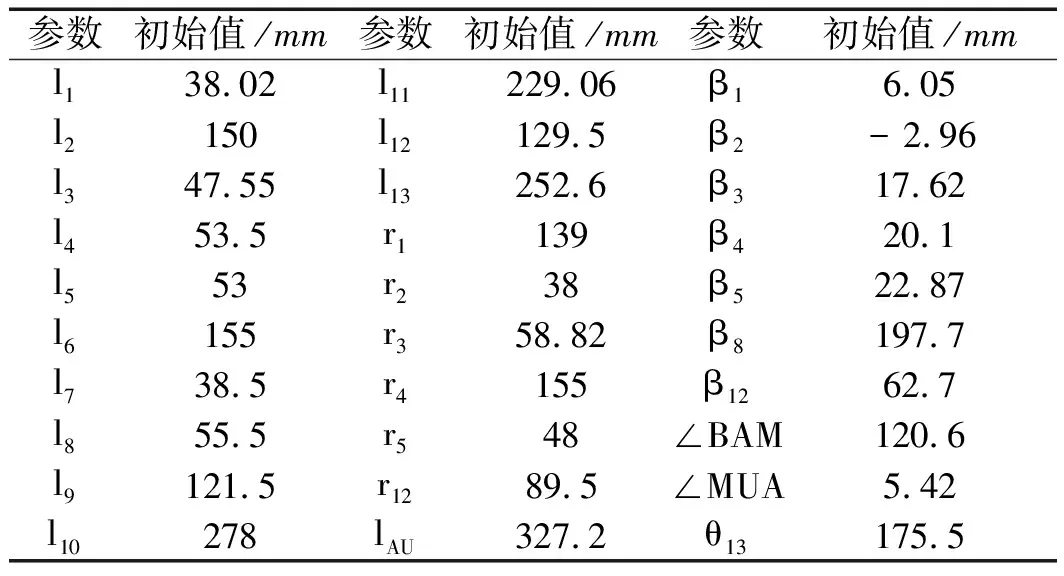
表4 杆件及结构角的初始值

图7 搁脚板角速度和质心速度曲线仿真值与理论值比较

3 结构参数优化

3.1 目标函数的建立

由于搁脚板在姿态变化过程中角速度和质心速度变化幅度较大而影响机构运动的平稳性，本研究以搁脚板运动平稳性为目标，建立目标函数。首先采用搁脚板质心速度的方差来建立目标函数[11]：

(17)

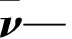
同理，可建立搁脚板角速度的表达式：

(18)

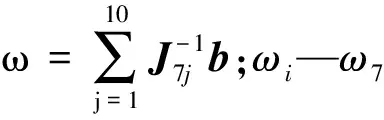
3.2 优化设计变量的选取

影响目标函数的参数量有杆件的长度li、ri及两者之间的结构角βi，由于结构角变化将导致搁脚机构伸展时结构发生干涉，结构角βi不作为优化设计参数。对变量进行灵敏度分析后，取对目标函数f1(x)与f2(x)的影响程度都较大的变量作为最终的设计变量，最终选取：

[X1，X2，X3，X4，X5]=[l4，l6，r3，r4，r5]

3.3 约束条件

(1)锁紧长度L：如图6所示，当电动沙发的姿态为坐姿时，搁脚板前端面到搁脚板与座板的连接点的距离L为：

55≤L=XJ0-XB0≤80

(19)

式中：XB0—坐姿时B点横坐标；XJ0—坐姿时J点的横坐标。

(2)根据人机工程学要求[12]，为了增加休闲姿的舒适性，伸展到位的搁脚板质心点J距离初始状态的J0的水平距离至少要达到440 mm才能在休闲姿时对小腿有很好的支撑作用：

440≤ΔXJ=XJt-XJ0≤465

(20)

式中：XJ0—初始坐姿J点X方向的坐标值；XJt—休闲姿J点X方向的坐标值。

(3)搁脚伸展到位时运动角度要求：

85°≤|θ7t-θ70|≤95°

(21)

式中：θ70—初始坐姿θ7的角度；θ7t—休闲姿时θ7的角度。

(4)休闲姿搁脚板到座板的高度差，转换为两铰接点的Y方向的距离，可表示为：

55≤YIt-YBt≤85

(22)

式中：YIt—休闲姿I点的纵坐标值；YBt—休闲姿B点的纵坐标值。

(5)杆长约束条件：

50≤l4≤70、149≤l6≤171、42≤r3≤63

138≤r4≤161.5、40≤r5≤56

(22)

4 Matlab优化结果

采用Matlab中的fmincon优化工具箱可以解决带非线性约束的优化问题[13]。用加权系数法可以将多目标问题转化为单个目标优化问题，取加权系数为0.6和0.4，可得到总的目标函数为：

f(x)=0.6f1(x)+0.4f2(x)

(23)

本研究将目标函数及约束条件在Matlab中进行编程，设计变量的上下限即为杆长约束条件，通过调用优化工具箱进行迭代运算得到最终的优化解[14-15]，优化后的参数如表5所示。

表5 优化后参数值

通过Matlab优化工具箱求解目标函数，将得出的优化参数代入Matlab的参数模型中，可输出得到搁脚板角速度与质心速度曲线。电动沙发结构参数优化前后搁脚板角速度和质心速度对比曲线如图8所示。

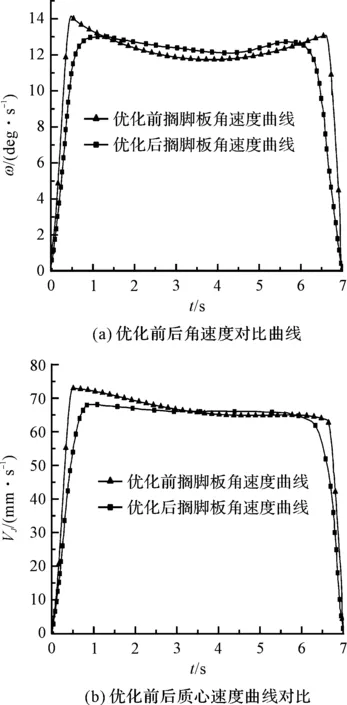
图8 优化前后搁脚板角速度和质心速度对比曲线

在实现机构由坐姿到休闲姿的转变过程中，优化前搁脚板质心速度及其角速度最大变动幅度分别为11 mm/s和3.5 deg/s，优化后两者最大变动幅度为4 mm/s和1.5 deg/s，由此，通过整个结构参数优化过程使得搁脚板在姿态变化过程中的速度平稳性得到了提升，提高了电动沙发的舒适性。

5 结束语

本文对电动沙发整机模型进行运动仿真分析，引出了休闲姿实现的过程中搁脚板角速度及其质心速度不平稳问题，采用复杂平面杆系运动学理论，对实现休闲位姿的复杂杆系建立理论模型，并求得其速度、角速度表达式；同时借助Matlab优化工具箱，以搁脚板的角速度和质心速度作为优化目标，求解出对目标函数影响大的杆长参数的最优解。

结果表明：连杆参数优化后的搁脚机构在姿态转换过程中速度的平稳性得到了增强，提高了电动沙发的舒适性。本研究可为同类型机构的设计优化提供参考。