用正弦定理研究满足“边边角”条件的两个三角形何时全等

甘志国

(北京市丰台二中 100071)

一、判定定理

众所周知，满足“边边角”条件(有两边和其中一边的对角分别对应相等)的两个三角形不一定全等，但有以下结论成立：

定理 有两边和其中一边的对角分别对应相等，且这两边中另一边的对角之和不为平角的两个三角形全等(简记为“SSA，B+B′≠180°”).

已知：如图1所示，在△ABC与△A′B′C′中，AB=A′B′,BC=B′C′,∠C=∠C′,∠A+∠A′≠180°.

求证：△ABC≌△A′B′C′.

证明 由正弦定理，可得

再由题设，可得sinA=sinA′，所以∠A=∠A′或∠A+∠A′=180°.

再由题设∠A+∠A′≠180°，可得∠A=∠A′.

进而可得△ABC≌△A′B′C′(AAS).

推论 有两边和其中一边的对角分别对应相等的两个三角形不全等的充要条件是这两边中另一边的对角之和为平角且另一边的对角不全为直角.

推论的意义即：如图1所示，在△ABC与△A′B′C′中，若AB=A′B′,BC=B′C′,∠C=∠C′，则△ABC与△A′B′C′不全等的充要条件是∠A+∠A′=180°且∠A≠90°.

二、判定定理的应用

题1 求证：等腰三角形的判定定理(等角对等边).

已知：在△ABC中，∠B=∠C.求证：AB=AC.

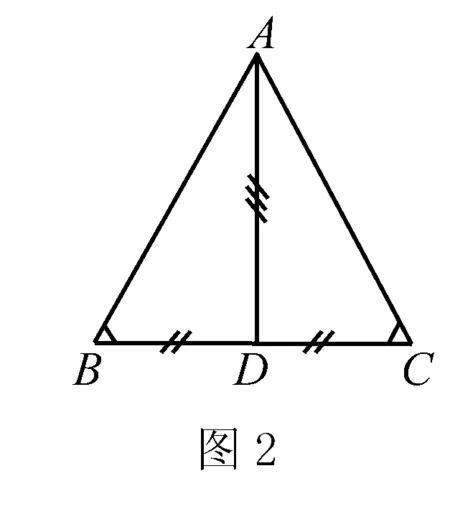
证法1 如图2所示，作∠BAC的平分线AD交BC于D.

可得△ABD≌△ACD，所以AB=AC.

证法2 如图2所示，作AD⊥BC于D，可得△ABD≌△ACD，所以AB=AC.

证法3 如图2所示，设边BC的中点是D，连结AD.

由定理可得△ABD≌△ACD，所以AB=AC.

证法4 如图2所示，作AD⊥BC于D，由∠B=∠C,得∠BAD=∠CAD.可得△ABC≌△ACB(ASA)，所以AB=AC.

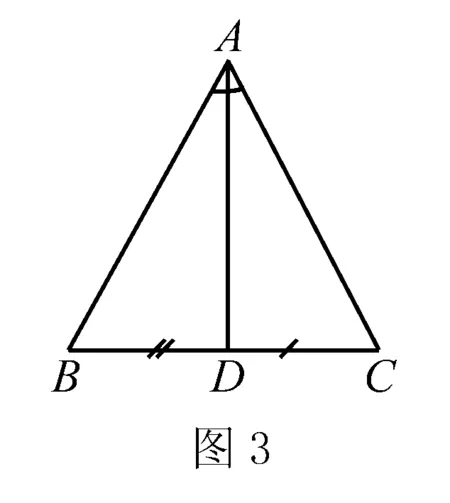
题2 已知：如图3所示，AD是△ABC的角平分线也是中线. 求证：AB=AC.

证明 由∠B+∠C<180°及定理，可得△ABD≌△ACD，所以AB=AC.

注 可证“两线合一推等腰”，但较难的是题2的结论.

题3 已知：如图4所示，点D,E均在△ABC的边BC上，AB=AC,AD=AE.求证：BD=CE.

证明 在△ABC中，由AB=AC，可得∠B=∠C.

由∠1+∠2<180°，可得∠3+∠4>180°.

再由定理可得△ABD≌△ACE，所以BD=CE.

题4 已知：如图5所示，AB=AC，△ABC的两条中线BD,CE交于点O.求证：点O在∠BAC的平分线上.

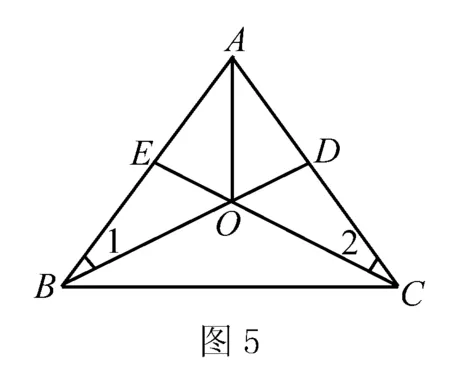
证明 可得△ABD≌△ACE，所以∠1=∠2.

又由∠BOC<180°，可得∠AOB+∠AOC=360°-∠BOC>180°.

再由定理可得△AOB≌△AOC，进而可得点O在∠BAC的平分线上.

三、一道反例的构造

题5 求作一个凸四边形，使其有一组对边相等且有一组对角相等，但这个凸四边形不是平行四边形.

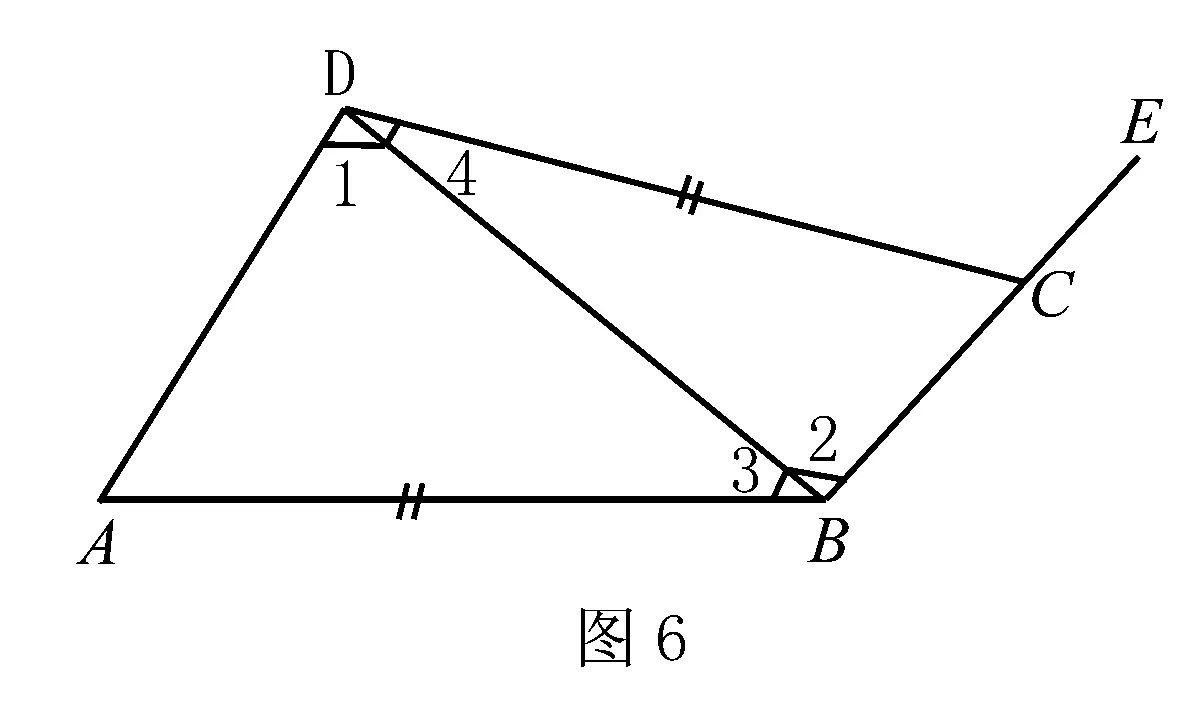
分析 如图6所示，要求凸四边形ABCD不是平行四边形，就是要求满足“边边角”的两个三角形(△ABD与△CDB)不全等.

由推论可得，其充要条件是∠1+∠2=180°且(∠1<90°或∠2<90°).

可不妨设∠1<90°,∠2>90°.在△CDB中，可得DC>DB，所以AB>DB.

又由∠ABC=∠2+∠3=180°-∠1+∠3<180°，可得∠1>∠3,AB>AD.

所以AB是△ABD的最大边，进而可得△ABD是锐角三角形.

从而可得如下：

作法1 (1)如图6所示，作锐角△ABD，且AB>DB,AB>AD.

(2)在△ABD外作∠DBE=180°-∠ADB.

(3)以点D为圆心，AB为半径作弧交射线BE于点C(因为可证得DC>DB，所以点C是唯一存在的).

(4)连结DC.

四边形ABCD就是凸四边形ABCD.

证明 只需证明∠ABC<180°,∠ADC<180°,∠A=∠BCD.

由AB>AD，可得∠1>∠3，即180°-∠2>∠3，所以∠ABC=∠2+∠3<180°.

由∠2>90°，可得∠2>∠4，即180°-∠1>∠4，所以∠ADC=∠1+∠4<180°.

由正弦定理，可得

sinA=sin∠BCD.

又由∠A,∠BCD都是锐角，可得∠A=∠BCD.