高中物理直线运动解题技巧探究

谢金池

(重庆市南开中学 400001)

直线运动是高中运动学比较简单的运动，一般会以地面为参照物.而对于两个或以上的物体运动问题，需要用到运动的合成与分解，参照物也可以选取有利于解决问题的物体.下面我就自己的总结，对直线运动的问题的解决技巧归纳如下：

一、运用基本公式解题

这类问题一般比较简单，根据已知条件进行问题的分析，正确运用公式就可以有效的解决问题.同时，选取正确的参照物和辨别试题中的干扰条件，可以提高正确率.

例题1 一辆汽车在平直的公路上以10m/s的速度匀速行使，这时其正前方出现一辆自行车，已知自行车以4m/s的速度与汽车做同向匀速直线运动，汽车立即刹车，以6m/s2的加速度匀减速行使，那么，汽车离自行车至少多远的距离才刚好不碰上自行车.

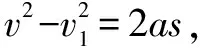
二、运用图像法解题

数形结合的思想在高中物理问题的分析和解决过程中也同样实用，对于一些过程复杂，运用代数方法不好解决的问题，我们可以试试借助图像的方法，通过图像的直观性将问题有效的解决.

例题 将物体A以初速度2v0由水平地面竖直上抛，然后将物体B以初速度v0由同样水平地面竖直上抛，如果物体A和物体B在空中相遇，在忽略空气阻力的情况下，二者抛出的时间间隔应该是多少？

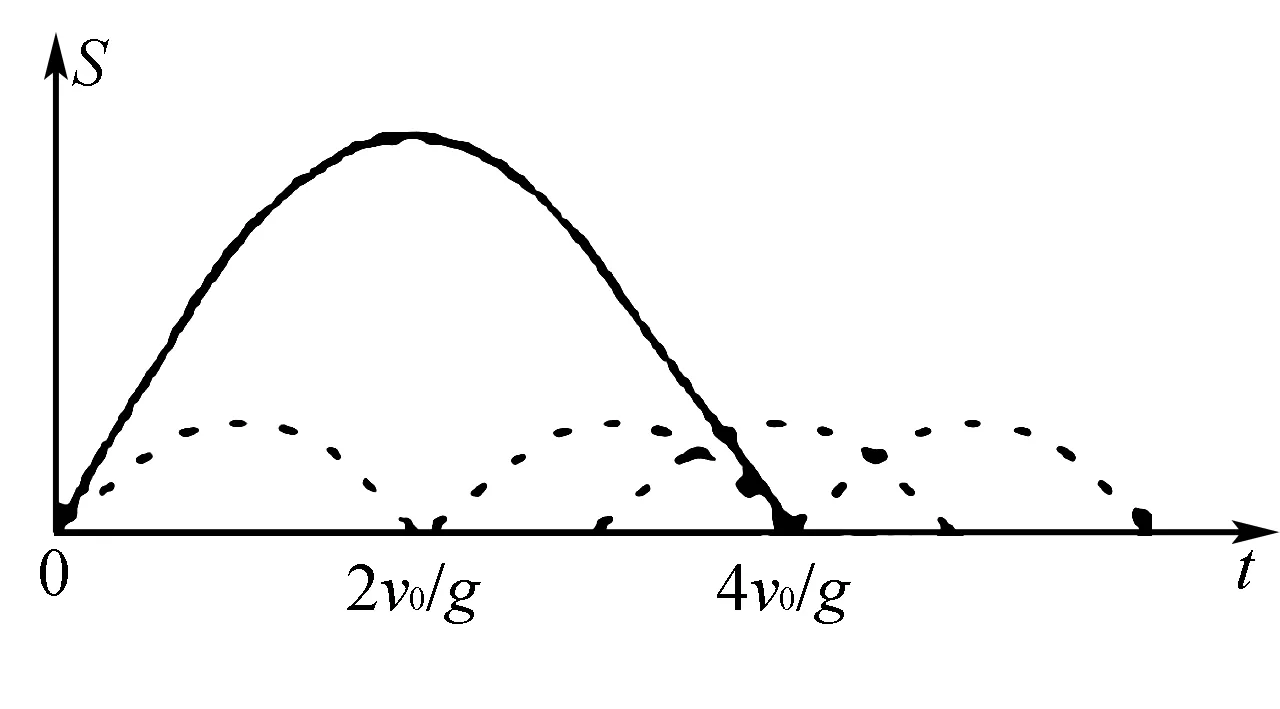
图1

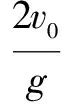
三、运用逆向思维解题

高中物理运动的过程很多时候是可逆的，对于一些直接不容易求出结果的问题，我们可以尝试逆向思维，从结果向过程推导，既能活跃我们的思维，也能有效的解决问题，提高解题效率.

例题3 已知一个物体做加速度a=10m/s2的匀减速直线运动，物体在停止前最后一秒的位移等于物体匀减速直线运动位移的一半，求物体在匀减速直线运动过程中的位移是多少？

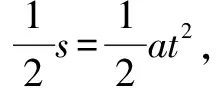
四、运用运动的分解与合成解题

运动是一个矢量，可以分解和合成，尤其是两个物体组成的系统或是两个物体独立运动的时候，正确的使用运动的分解与合成，可以将未知的问题转化为已知的问题，从而有效的解决问题.

例题4 已知物体A与B通过不计重量，长为100m的轻质细绳相连，现在从同一个高度以3m/s的初速度将物体A竖直下抛，同时以4m/s的初速度将物体B水平抛出，忽略物体运动过程中的阻力，那么，经过多长时间以后轻质细绳会被拉直.已知g=10m/s2，轻质细绳拉直前A物体没有落地.

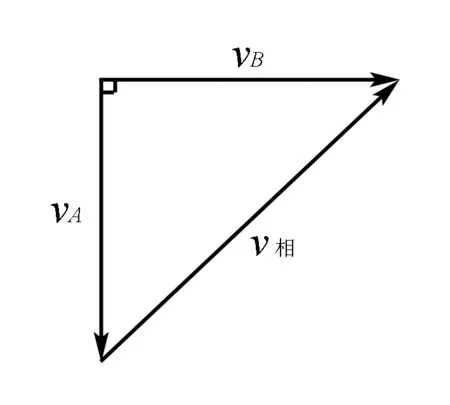
图4

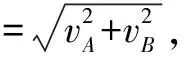
五、运用中间变量解题

有时候一些物理问题可以转化为中间变量，既简单又方面.因此，对于不能直接求解，或是直接求解比较麻烦的问题，我们可以通过中间变量的运用，有效的解决问题.

例题5 从高为105米的房顶以初速度20m/s竖直向下抛出一个小球，忽略空气阻力的情况下，求小球落地前最后一秒通过的位移？(g=10m/s2)

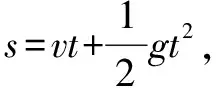
总之，高中物理是一门比较抽象的学科，但是物理知识有其自身的规律，我们在学习的时候，要结合物理知识的规律不断的分析和总结，归纳出有效的解题方法，既可以帮助我们脱离题海战术，又能提高我们的学习效率.