“亚黄金椭圆”的新定义及性质
2018-12-27 08:31:04刘娟娟罗文军
数理化解题研究 2018年34期
刘娟娟 罗文军
(1.甘肃省秦安县郭嘉镇槐川初级中学 741609;2.甘肃省秦安县第二中学 741600)
笔者在文[1]中给出了亚黄金椭圆的5个性质,为本文的性质1到性质5.在文[2]中给出了亚黄金双曲线的定义和6个性质,在文[3]中又给出了亚黄金双曲线的8个性质.
笔者在教学之余又得出了亚黄金椭圆的新定义及3个性质,3个性质为本文中的性质6到8现.介绍如下以供参考.
为了本文探讨亚黄金椭圆性质的需要,这里须对一些概念作些说明.
黄金矩形的定义:
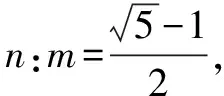
为了以下性质探究的方便,在不影响亚黄金椭圆性质的条件下,做两点假设:
第一,以椭圆的中心为原点,两焦点所在直线为x轴建立直角坐标系;
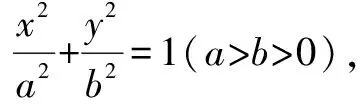
一、亚黄金椭圆的新定义
二、亚黄金椭圆性质的探究
性质1 在亚黄金椭圆中,两条互为共轭直径所在直线的斜率(斜率存在)之积为-e4.
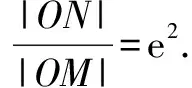
性质3 不平行于亚黄金椭圆对称轴的切线斜率与经过该切点和中心的直线斜率之积为-e4.
性质4 不平行于亚黄金椭圆对称轴且不经过椭圆中心的弦所在直线的斜率与经过该弦中点和椭圆中心的直线斜率之积为-e4.
性质5MN是经过亚黄金椭圆中心的弦,T是亚黄金椭圆上任意一点(顶点除外),如果TM,TN的斜率都存在且不为0,则kTM.kTN=-e4.
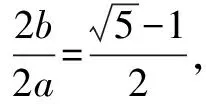
所以由直线x=a,x=-a,y=b,y=-b所围成的矩形为黄金矩形.
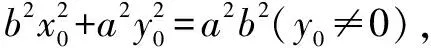
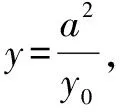
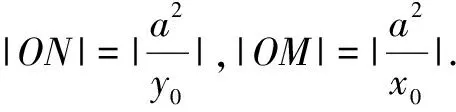
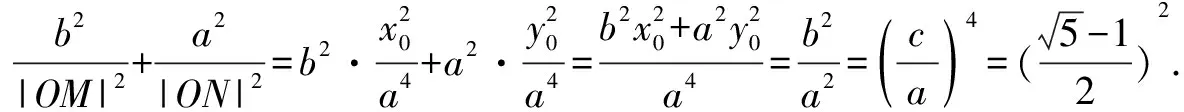
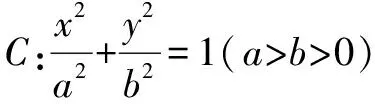
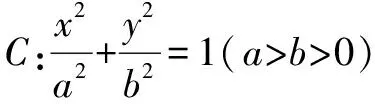
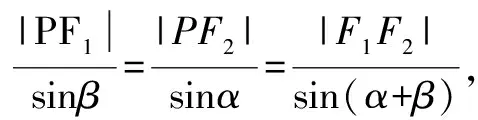
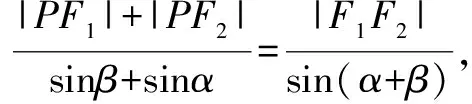
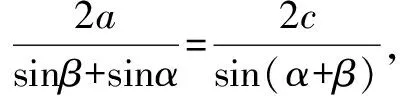
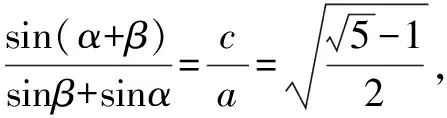
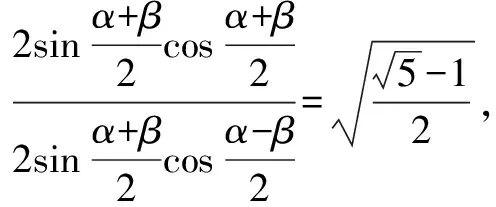
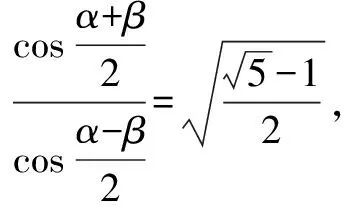
由合分比定理得
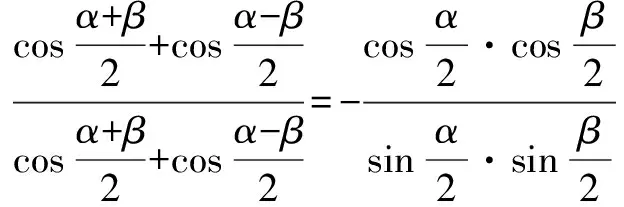
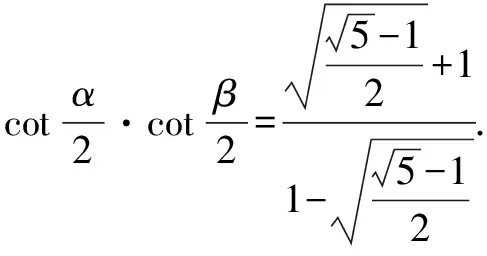
猜你喜欢
甘肃林业(2022年4期)2022-08-15 14:00:20
甘肃林业(2021年5期)2021-10-18 05:07:48
数学年刊A辑(中文版)(2020年2期)2020-07-25 02:04:36
物理之友(2020年12期)2020-07-16 05:39:16
学生天地(2020年28期)2020-06-01 02:18:46
中学生数理化·七年级数学人教版(2019年4期)2019-05-20 10:03:44
中学生数理化·八年级数学人教版(2017年4期)2017-07-08 13:04:56
学生天地(2017年8期)2017-05-17 05:49:48
福建中学数学(2016年7期)2016-12-03 07:10:28
光学精密工程(2016年1期)2016-11-07 09:01:53

