初中数学教学中的类比法运用

刘 勇

(江苏省南通市实验中学 226001)

一、运用类比进行知识联系的构建

1.类比生活实际

将学生熟悉的生活背景与数学知识融合在一起并通过类比教学能使学生更好地掌握数学的本质与模型.

例如，教师在“合并同类项”这一内容的教学中可以创设以下情境：

(1)实物归类：教师首先将形状为圆、方形、三角形等学习用品混在一起，请学生根据自己的标准将这些学习用品进行分类并要求学生回答如下问题：①你是根据什么标准进行分类的？②分类标准一样的情况下分类方法唯一吗？③你心中的分类方法有哪些？

(2)观察多项式-2x+8y-4z+x-y并回答以下问题：①哪几项可以归为一类呢？②你分类时的依据是什么？那么3a2b-4ab2-3+5a2b+2ab2+2ab-6ab+8应怎样归类呢？

学生在实物分类到数学分类的活动中往往会感到数学的可亲可近，数学的神秘和抽象对于学生来说也随之消除很多，学生在熟悉的生活背景下对类比法也形成了更加真切的感受与理解，数学和实际的联系也因此得到具体的体现.

2.类比旧知

运用类比法进行新概念的引入往往能令学生对新概念的内涵与外延形成更好的理解，数学概念的类似也在类比法的运用中而变得更易理解与掌握.

例如，教师在教学“分式”这一内容时可以首先利用类比分数的方式导出分式的概念、分式的基本性质与运算法则.具体操作如下：第一步，引导学生回顾小学阶段学过的分数的概念；第二步，回顾分数的构成以及分母不能为零的特点；第三步，回顾分数的分类并将分数的概念延伸到代数式中，继而获得分式的概念；第四步，在学生掌握分式概念的基础上明确分数和分式之间的区别.

二、在类比中锻炼学生思维

1.类比操作

例如，教师在“角的比较与运算”这一内容的教学中可以这样落实类比操作：首先引导学生对线段的比较方法进行复习与回顾，然后引导学生尝试对两个角的大小进行比较，学生在教师的这种类比操作中自然会联想到线段比较中的度量法与叠合法，最后，教师再引导学生对角的比较法与注意事项进行归纳时，学生在一定的经验与知识基础之上进行总结与归纳也就水到渠成了.

2.类比计算

例如，学生在六十进制的角的度数换算中往往会觉得颇有困难，因此，教师可以引导学生在以下的设计中充分运用类比计算进行学习：

第一步：计算：0.8米=____分米，0.8小时=____分钟，引导学生对这两个计算进行观察并发现其共同点，使学生建立高级单位向低级单位换算需要乘以进率的概念.

第二步：计算：0.8°=____′，5′=____″.学生在这样的计算经历中自然会联想到类比法，反向亦是如此.先请学生计算30分米=____米，30分钟=____小时.

第三步：引导学生对低级单位向高级单位转换的规律进行自主归纳并进行一定的换算运用.

3.类比探究

例如，“线段”这一内容中的一道题：若一线段上有n个点，则共有多少条线段呢？

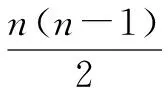
“一元二次方程”中的一个问题也可运用类比思想进行解决：出席某次聚会的每位代表都会与其他各代表均握手一次，统计结果为共握手45次，则参加聚会的代表共有多少呢？

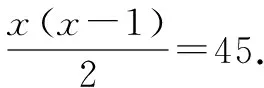
上述两个问题虽然有一定不同，但其本质却是相同的，学生在解决第一个问题的基础上再求解第二个问题也会容易很多.

4.类比归纳

对两种或两种以上在某些关系上具备一定相似特征的对象进行对比与归纳的研究方法即为类比归纳，学生在知识的类比与归纳中往往能将知识体系构建得更加有序和系统.

例如，教师在“一元一次不等式的解法”这一内容的教学中可以首先对一元一次方程的解法进行复习，然后引导学生对一元一次不等式的解法进行讨论，使学生在类比讨论中获得其解法与步骤.

5.类比猜想

运用类比对两个对象或问题的相似性进行比较并获得数学新命题或方法的猜想即为我们经常运用的类比猜想，对命题本身或解题思路方法进行类比继而产生猜测都是获得命题推广与引申的原动力.

例如，教师在“等腰梯形同一底边上的两底角相等”这一内容的讲授中，首先可以引导学生对“等腰三角形的性质”进行回顾，然后引导学生在此基础上上进行类比猜测并加以验证.

由此可见，发现解题思路、导入新概念、记忆与证明公式定理、探索研究新知识等数学学习的多个方面都需要运用到类比法，类比法在数学教学中的运用对学生的知识建构、能力发展都能起到很好的作用.因此，教师应充分认识到类比法的价值，根据不同的教学对象落实不同的类比方法以促进学生知识与能力的发展.