勾股定理及其教学方法探微

池洛阳

(江苏省新沂市瓦窑中学 221400)

一、勾股定理的内涵和应用

1.勾股定理的内涵

勾股定理，又称毕达哥拉斯定理，是人类最早证明并应用于实践的数学定理之一.从希腊的毕达哥拉斯，到埃及金字塔时的建造，再到我国古代数学著作《周髀算经》，都能看到勾股定理的身影.

对于勾股定理的表述，一般为a2+b2=c2，其中，a、b是直角三角形的两条直角边，c是其斜边.勾股定理的逆定理，往往也被作为勾股定理的一部分.在现行教材中，特别将“勾股定理的逆定理”作为“勾股定理”这一章下的第二节进行编排.其具体表述则为：“如果三角形两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形，且最长边所对角为直角”.勾股定理：△ABC为直角三角形⟹a2+b2=c2，及其逆定理：△ABC为直角三角形⟸a2+b2=c2，也可以看作是学生最早接触的一个充分必要命题.

2.勾股定理的应用

勾股定理及其逆定理，以及其证明过程中的多种数学思想，在初中数学中的应用，也是极为广泛的.

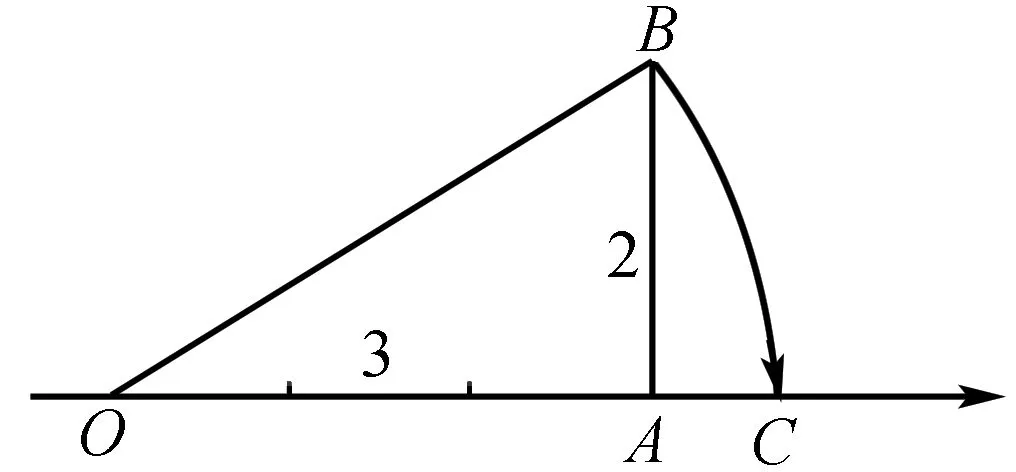
图1

图2

二、勾股定理教学方法策略

勾股定理的教学重点和难点，不止于勾股定理及其证明过程，如何吃透、消化勾股定理及其证明所蕴含的数学意义与数学思想，才是勾股定理教学中最为重要和最为困难的部分.

在实际教学中，我们应当抓住以下几点，以帮助学生更好地理解勾股定理的内涵与思想.

1.渲染数学文化构筑课堂，在浓厚学习兴趣中开展学习

前文提及的勾股定理及其证明，不论定理本身的表述，还是定理的证明过程，都过于抽象和略显脱离实际，这是不利于初中学生积极学习和充分理解的.因此，在课堂开始之初，渲染浓厚的数学文化氛围，激发学生的学习兴趣，是极为必要的.

教师可以在课堂之初，介绍毕达哥拉斯及其证明：“同学们，你们可以想象得到吗？在距今4000多年前，巴比仑人已经发现了勾股定理.古希腊的一位名叫毕达哥拉斯的学者，在2500年前完成了该定理的证明.而伟大的几何定理，它被用在了古埃及金字塔的建造之中，也在世界各地，几乎是每时每刻都发挥着巨大的作用，而它也是我们今天所要学习和掌握的定理，这就是勾股定理——也被称为毕达哥拉斯定理.”这样，学生对于勾股定理的研究兴趣，就自然而然地提升了起来.

除此之外，通过《周髀算经》或《九章算术》中的文言文，打开课堂教学也是可行的：“同学们，老师在最近遇到了一段文言文，不知道该怎么翻译，请问哪位同学可以帮老师翻译一下呢？”然后出示：“勾股各自乘，并之为弦实”，从而引入勾股定理的学习.

2.鼓励学生实践证明过程，在回顾前人思想中打牢基础

勾股定理及其证明过程，包涵诸多数学方法及数学思想，这往往是初中学生所欠缺的.因此，鼓励学生亲自推演勾股定理的一些证明过程，回顾、思考前人的睿智思想，是有助于其理解和掌握勾股定理的.

需要注意的是，要求学生实践这些证明方法，不是要他们简单地亦步亦趋地抄抄了事，而是要反复咀嚼，多加思考，教师也应多多提示，每一步的目的和蕴含的思想，都要针对性地拆解开来，在整个证明过程都吃透了之后，再让学生独自证明，真正做到“钻进去，走出来”.

3.利用相关问题实例，在不断思考练习中彻底掌握

举出一定的题目与实例，帮助学生加以训练，也是极为必要的.考虑到勾股定理在初中数学中的重要地位，关于勾股定理的题目数不胜数，但这也意味着质量上有所差距，教师在选择题目时，应当时刻注意题目所要考察的知识点与学生能力，不能大搞题海战术.

在选择相关题目时，一定要注意题目是否能够考察学生数形结合思维，在表面问题之上构筑直角三角形，将看似不相干的问题转化为勾股定理问题等能力素质，只有这样的题目，才能真正帮助学生彻底掌握勾股定理及其相关思想方法.

勾股定理作为几何学中最为基础和重要的定理，在初中数学中的地位不言自明.因此，在实际教学工作中，教师一定要帮助学生吃透这一重要定理，把握住其包涵的数学思想和方法，为日后的进一步学习打下坚实的基础.