也谈初中数学中“圆”的妙用

黄小燕

(江苏省常州市溧阳市第五中学 213300)

一、问题背景

从事初中数学教学多年，研究了很多题，也教会了学生很多方法和技巧，学生不仅在考试中可以考到较好的成绩，而且在做题过程中也积累了许多经验，体会到了一些好方法的乐趣.现在全国的中考数学卷中，圆的问题都不少见.

二、一般策略

那主要考查圆的哪些知识点和方法呢？

1.角的运算

涉及圆心角，圆周角关系定理.

2.线段长的计算

涉及垂径定理，切线的性质与判定定理，切线长定理，求圆中的弦长一般考虑作弦心距，构造直角三角形，用勾股定理进行运算.

3.位置关系

涉及点与圆，直线与圆.

4.圆与其它图形的综合运用

涉及勾股定理，相似等多种方法

三、圆的“妙用”

1.线段相等→圆

例1 如图，在四边形ABDC中，AB∥CD,AC=BC=DC=4，AD=6，则BD=____.

思路一构造全等三角形和直角三角形，如图1.

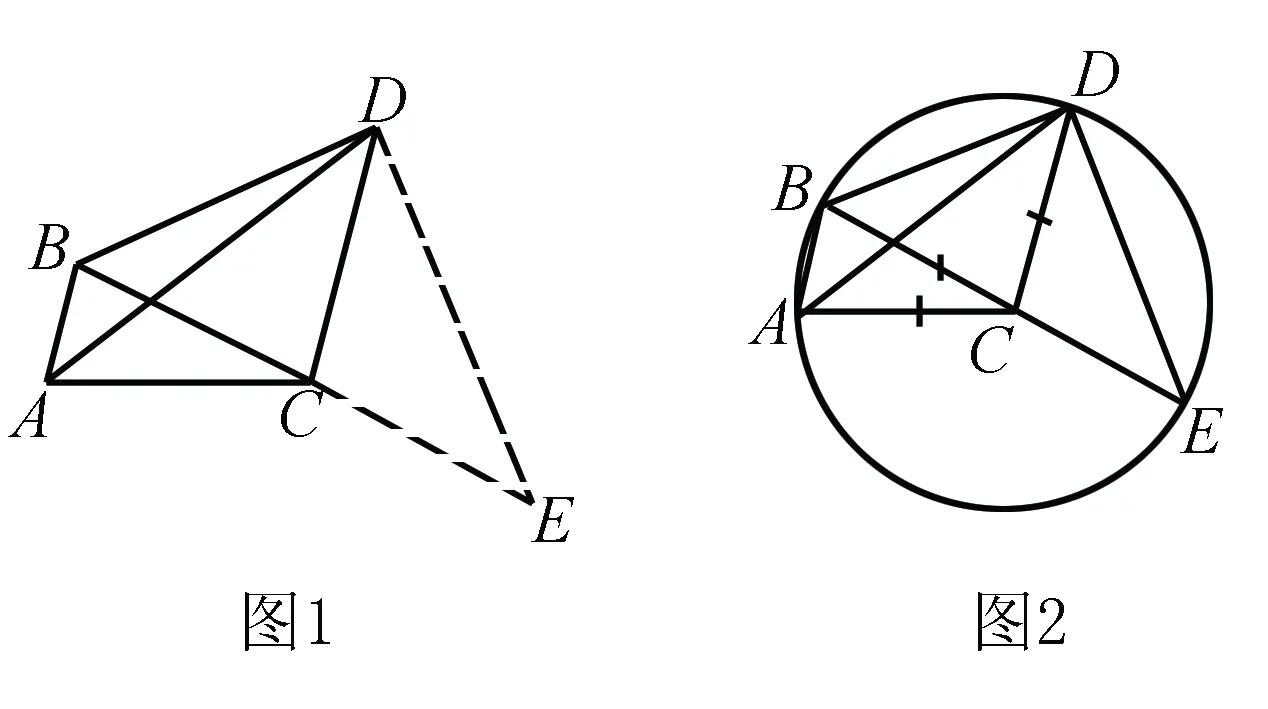
思路二由圆构造直角三角形

如图2，由AC=BC=DC知点A,B,D在同一个圆上，所以经常由点构圆，而根据直径所对的圆周角是直角即可构造直角三角形.

解∵AC=BC=DC，以点C为圆心，AC长为半径作圆C.延长BC交圆C于点E，连接DE，则∠BDE=90°，BE=8，AC=BC=DC=EC.

∵AC=BC，∴∠ABC=∠BAC.

∵AB∥CD，∴∠ABC=∠DCB=∠BAC，∠BAC+∠DCA=180°.

又∵∠DCB+∠DCE=180°，∴∠DCE=∠DCA.

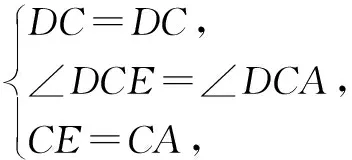
∴△DCE≌△DCA(SAS)，∴AD=ED=6.

2.直角→圆

(1)求线段最值

例2 如图3，直角三角形ABC中，∠ACB=90°,AC=6,BC=4,在△ABC内部以AC为斜边任意作Rt△ACD，连接BD，则线段BD长的最小值是____.

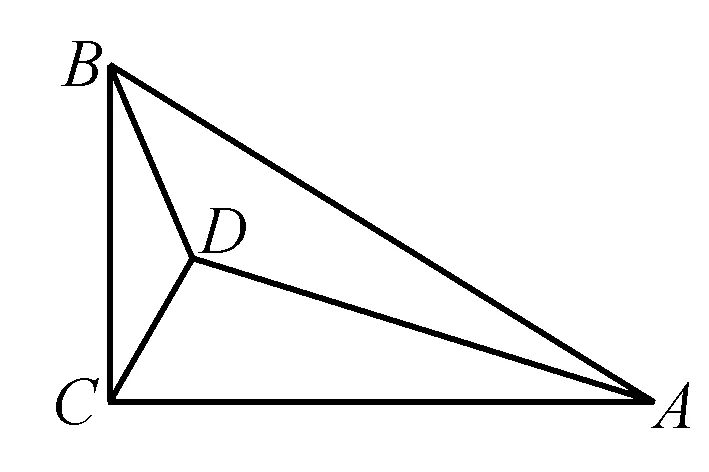
图3

分析此题解决的关键是要认识到点D始终是Rt△ACD的直角顶点，根据“90°的圆周角所对的弦是直径”推断AC是圆的直径从而找出圆心O，就知道了点D是在线段OB上.

解取AC的中点O.

在△ABC内部以AC为斜边任意作Rt△ACD,

则点D在以AC为直径的圆上，

∴当D点在OB上时，BD的值最小.

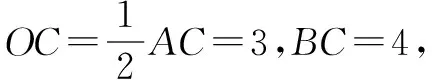
(2)利用圆找等角

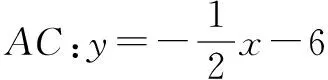
①连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标;

②在①的前提下，y轴上是否存在一点H，使∠AHF=∠AEF？如果存在，求出此时点H的坐标;如果不存在，请说明理由.

分析看到此类角相等，只有角的顶点不同，通常会联想到圆中的圆周角，所以点A,E,F,H在同一个圆上.而由图猜想并验证出∠EAF=90°，则圆被确定.

解②存在．

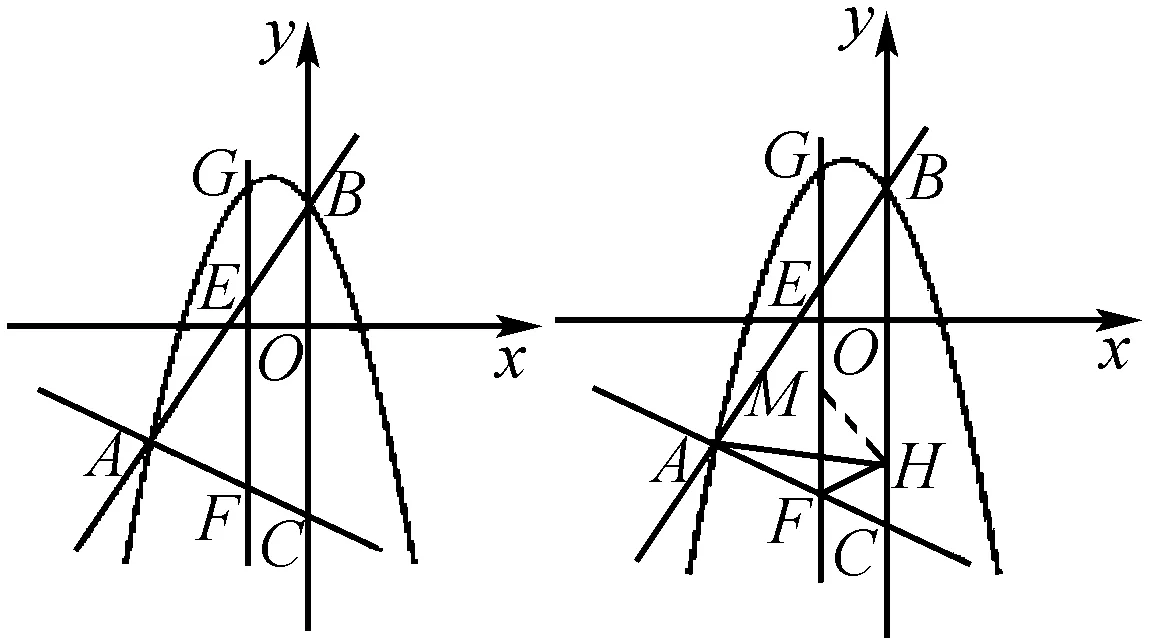
图4 图5

由①可知G(-2，4)，∴E(-2，0)，F(-2，-5).

∵AE2=42+22=20，AF2=12+22=5，EF2=52=25,

∴AE2+AF2=EF2.∴△AEF为直角三角形，∠EAF=90°,∴点A在以EF为直径的圆上.

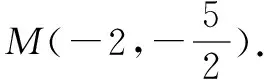
(3)利用圆作图

例4 在四边形ABCD的AB边上任取一点E(点E不与点A、点B重合)，分别连接ED、EC，可以把四边形ABCD分成3个三角形．如果其中有2个三角形相似，我们就把点E叫做四边形ABCD的AB边上的相似点；如果这3个三角形都相似，我们就把点E叫做四边形ABCD的AB边上的强相似点．

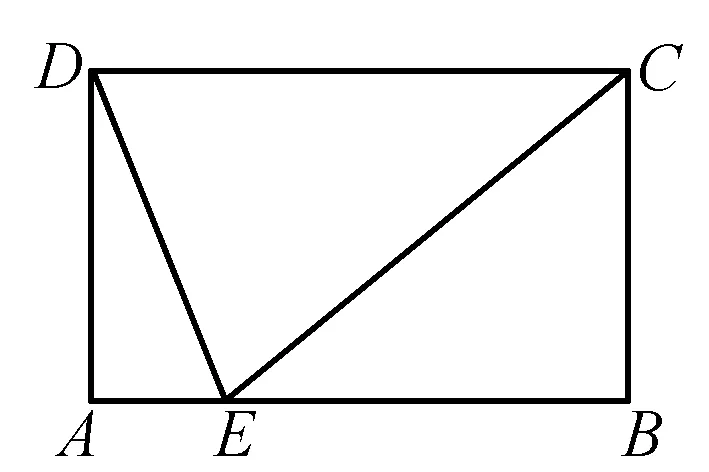
图6

如图6，画出矩形ABCD的AB边上的一个强相似点．(要求：画图工具不限，不写画法，保留画图痕迹或有必要的说明．)

分析以CD为直径画弧，取该弧与AB的一个交点即为所求．(说明略)

圆只是初中数学浩瀚知识海洋中的一隅，但与其它知识也紧密相连，学任何知识只要理解其本质，关键时刻就可融会贯通，事半功倍.学生不仅在中考中可获得满意的成绩，更能通过解题方法技巧经验的提炼和积累，体会成功的乐趣.