浅析初中生几何思维能力的培养方法

张 红

(江苏省连云港市东港中学 222042)

数学思想和思维能力是学生数学素养的具体体现，在初中数学教学中培养学生的逻辑思维能力需要教师因势利导，遵循学生的认知规律，引导学生对几何概念进行分析和推导，通过推理、判断来认识几何内容的性质和应用，锻炼学生的思维能力.这不仅有利于学生主动性发挥，发现几何规律，牢固的掌握几何知识，同时也能激发学生的探究兴趣，运用数学思想进行实际问题的解决，促进学生的几何思维能力的不断提升.

一、数形结合，培养学生几何思维能力

几何知识是初中数学教学的重要组成部分，初中阶段的几何主要是平面图形与代数知识的结合，对学生的数形结合思维能力有较高的要求.因此，初中数学教师要在教学中注重对学生进行数形结合思想的渗透，让学生能够将数学的“数”与“形”统一起来，通过“数”和“形”来进行几何知识的理解，往往能够起到良好的教学效果，也能增强学生的几何观念，培养学生的几何思维能力.

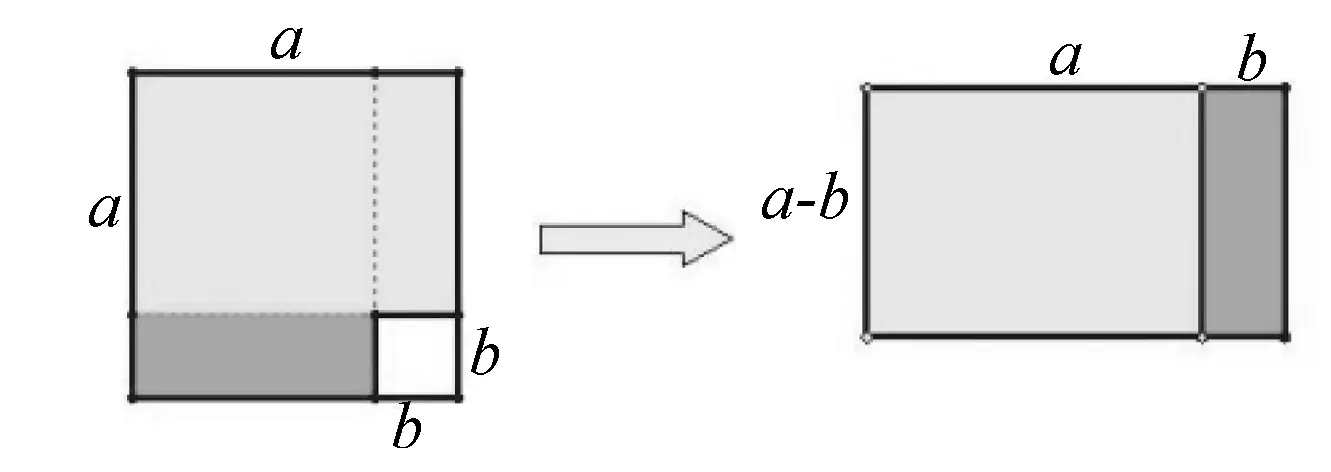
数形结合是提升学生几何思维的有效途径，图形可以将几何抽象的知识直观地表现出来，让学生进行直接的观察，简化复杂的推理和计算过程，更有利于学生的理解.比如在进行“平方差公式”学习的时候，教师可以让学生借助右图，运用割补法让学生直接理解a2-b2=(a+b)(a-b)的含义.反过来“数”可以弥补图形数量的关系，让学生通过数来理解图形中的隐含条件，掌握几何知识的学习和探究规律.以“角平分线的性质”为例，教师可以让学生进行实践活动，用纸裁剪一个任意角，将这个角对折，然后以角的一边为直角边折叠出直角三角形，之后展开.教师引导学生对折痕进行观察和测量，让学生互相交流，通过实践进行角平分线的性质推导，既能丰富教学内容，也能提升学生的几何思维能力.

二、分类讨论，培养学生的发散思维能力

分类讨论思想在初中几何学习和问题的分析、解决过程中有着广泛的应用，是解决初中几何图形位置不确定或是图形形状不确定问题的重要思想方法.分类思想主要是针对问题的不确定性，按照不同的情况对问题进行分类，然后再逐步地解决各类情况的问题.需要注意的是运用分类讨论思想进行分类的时候要同一标准进行；分类应逐级进行；同级互斥、不得越级.这样才能将所有情况都分析到，避免多项和漏项.初中数学教师要结合教学内容，对学生进行分类讨论思想的渗透，促进学生的思考，不断提升学生的思维能力，促进学生的发展.

比如在进行三角形有关问题教学的时候，教师就可以结合等腰三角形的性质引导学生运用分类讨论思想进行分析和探究，培养学生的数学思想意识，锻炼学生的思维能力.

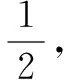
分析本题中的等腰三角形并没有配图，BC边是腰还是底不能确定，因此教师要让学生分别从腰和底两种情况进行讨论，当BC边是腰的时候，由于顶角的不同情况，高线的位置也不同，因此会导致∠BAC的度数不确定，这就要求学生需要根据锐角、直角和钝角的情况进行讨论.

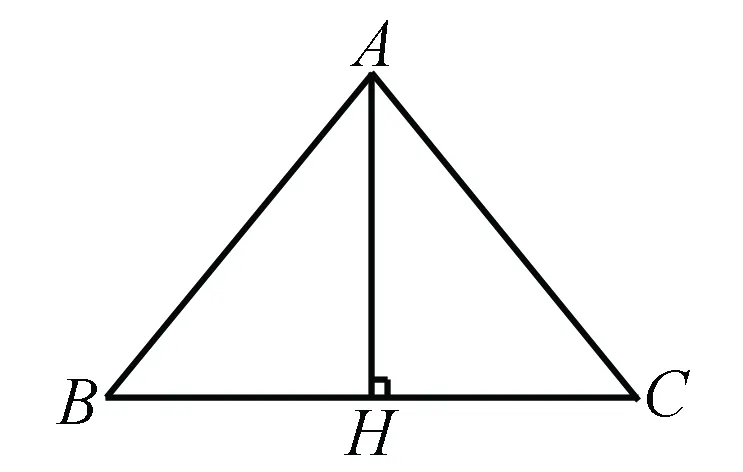
当BC边为底边的时候(如右图)，根据等腰三角形的性质，AH三线合一，根据已知BC=2AH可知高线所分出的两个三角形全等，由此可知∠BAC为直角.

当BC边为腰的时候，需要根据顶角的情况进行分析(如下图)，当∠ABC为锐角的时候，高线在三角形内，根据等腰三角形两腰相等，高线垂直腰可以得出∠ABC=30°；当∠ABC为直角的时候，高线与三角形AB边重合，这就与已知条件矛盾，因此不存在满足条件的三角形；当∠ABC为钝角的时候，高线在三角形外，根据已知条件可以求出∠ABC为150°，问题也就迎刃而解了.

分类讨论思想在初中几何三角形、线段和角等知识中都具有广泛的应用，在教学中对学生进行分类思想的渗透，可以发展学生的思维，帮助学生养成从多角度、多层面进行问题的分析和探究习惯，从而既让学生掌握初中几何知识，也能有效地促进学生的思维发展.

总之，初中数学教学在教学中要以教材几何知识为依托，通过数学思想方法的渗透发散学生的思维，让学生能够从不同的角度进行问题的分析和解决，并引导学生互相借鉴和参考，锻炼学生的思维能力，同时教师也要对学生多进行引导，深化学生的思维能力，培养学生的数学素养.