从几对似同实异的题目说起

孙夏珍

我们都知道解题离不开思维，却不一定知道“解题”与“思维”哪个是手段哪个是目的.有人认为训练思维的目的是为了解题，于是题目解完了就算大功告成了，就立即去解下一道题了.实际上解题只是手段，训练思维才是目的，因而解题过后的反思必不可少.

有些同学颠倒了手段与目的的关系，变成了为解题而解题，热衷于“题型训练”，只想着“套解法”.这样做的后果，很可能是在平时确实“掌握”了不少题型，但在应用的时候连“题型”都识别不清，遑论复杂情境下的变形与转换了.数学上有些题目，形式上非常相近本质上却相差甚远，是很容易张冠李戴的，只有在思维上训练有素才能认清它们.

一、“当”与“仅当”

例1（A）若当x＜1时，表达式lg（1+2x+3x+4x a）有意义，请研究a的取值情况.

（B）若仅当x＜1时，表达式lg（1+2x+3x+4x a）有意义，请研究a的取值情况.

说明这是两个完全不同的题目，仅从答案你就能看到二者间的巨大差异：（A）的答案是一个范围（B）的答案是一个值.详解如下：

解（A）“当”x＜1时，表达式lg（1+2x+3x+4x a）有意义，即∀x∈（-∞，1），恒有成立，即恒成立.左边为减函数，故，从而知，即.

（B）“仅当”x＜1时，表达式lg（1+2x+3x+4x a）有意义，则除了上面“当”的条件而外，还有“当x≥1时，表达式lg（1+2x+3x+4x a）恒无意义”，即 ∀x∈ （-∞，1），恒有1+2x+3x+4x a≤0成立.这时仿照上面的过程可求得.综合知.

注意，这里“当”给出的是一个充分条件，“仅当”给出的是一个充要条件.“仅当”实际上相当于逻辑用语中的“当且仅当”，后者更明显地突出了“充分”和“必要”两个方面的要求，因而更为人们所喜闻乐见.

二、“存在”与“任意”

例2椭圆L的焦点是F1（-3，0），F2（3，0）.

（A）若点P在L上，则，求L离心率的取值范围.

（B）若点P在L上且，求L离心率的取值范围.

说明你能体会到两个小题之间的差异吗？为便于比较，我们同样先给出答案，如下：（A）

解设P（x，y），则由得 （-3-x，-y）·（3-x，-y）≤7，化简得x2+y2≤16，即点P的轨迹是一个圆及其内部.设L的方程为0），且c＝3.如图1所示.

（A）若点P在L上，则，则L上的任意点都在上述的圆及其内部，故a≤4.从而知，即离心率的范围是

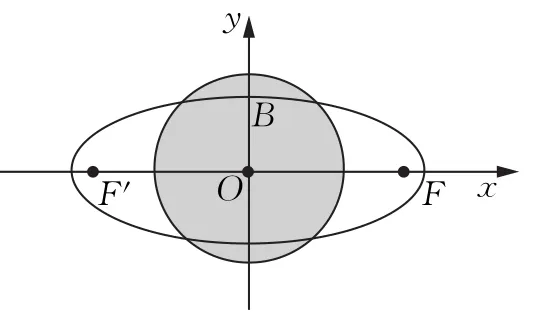
图1

（B）点P在L上且，意为L上存在点P满足所述的条件，即b≤4，从而a≤5.故，即离心率的范围是

三、“连续”与“离散”

例3（A）函数（λ是常数，λ∈R）在[1，+∞）上单调递减，求λ的取值范围.

（B）数列｛an｝的通项公式是an＝（λ是常数，λ∈R），若｛a｝是递减数n列，求λ的取值范围.

解（A），因为函数在[1，+∞）上单调递减，故f′（x）≤0，即得-x2+2x-λ≤0恒成立（当x∈[1，+∞）时）.即λ≥-x2+2x，从而λ≥1.

（B）解法1参照（1）中的解答过程，知只要函数在[2，+∞）上单调递减且f（1）＞f（2），即得.

解法2因为｛an｝是递减数列，故∀n∈ N*，恒有an+1＜an成立，即，变形为λ＞，即得.

说明这里的（2）很容易被误以为等价于（1），但从解答过程里我们可以看到它们的截然不同.连续曲线的上升与下降，不同于离散点的上升与下降，在周期性循环的曲线上，我们也可以找出上升或下降的点列，这给我们提供一个思考用的背景图.需要说明的是，我们时常会有“连续自然数”和“连续正奇数”之类的说法，这又加大了把离散变量与连续变量相混淆的可能性.如果我们用另一个更常见也更显简单的题目来说明，可能更容易理解.比如下面这个题目：

数列｛an｝的通项公式是an＝n2+λn+2（λ是常数，λ∈R），若｛an｝是递增数列，求λ的取值范围.（答案：λ＞-3）

四、“某点处”和“过某点”

例4（A）已知曲线y＝x3-3x+2，求点P（2，4）处的切线方程.

（B）已知曲线y＝x3-3x+2，求过点P（2，4）的切线方程.

解（A）y′＝3x2-3，故点P（2，4）处的切线斜率k＝9，从而得切线方程是y-4＝9（x-2），即9x-y-14＝0.

（B）设切点坐标为A（x0，y0），则点A处的切线 方程是.将点P的坐标代入得，即1）＝0，从而知x0＝2或x0＝ -1，即得切点坐标为（2，4）或（-1，4），易得切线方程是9x-y-14＝0或y＝4.

说明“某点处的切线”和“过某点的切线”，在一种情况下尤其会引起混淆，那就是这个“某点”本身就在曲线上.从这里的（B）我们应该看到，即使这个点在曲线上，也可以不是切点（如图2）.明白了这个，混淆就基本消除了.过三次函数图象上的一点，有可能作出两条切线；过正弦曲线上的一点，有可能作出无数多条切线.

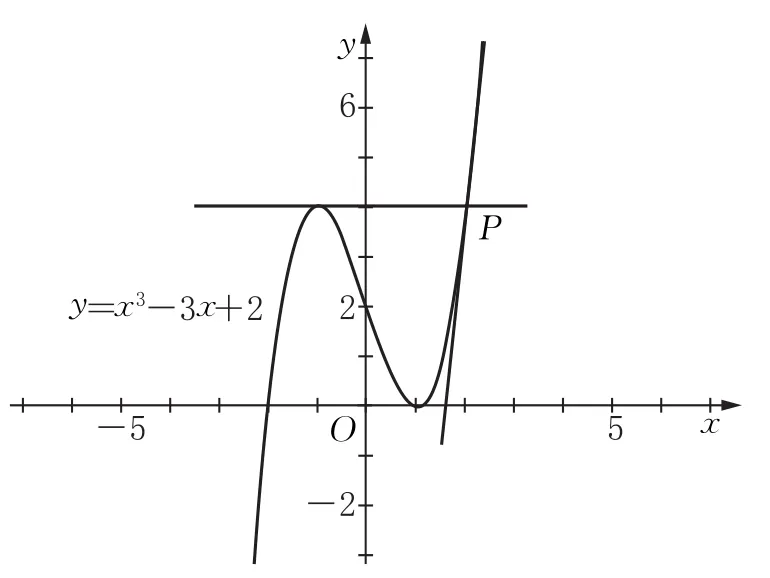
图2

五、“可以是”与“必须是”

数学题中不会有 “可以是”与“必须是”这样的说法，它们不是数学的规范用语但是在生活中常用.也许正因为这样，我们对此没有养成足够的敏感，在解题操作的过程中会不慎“窜入”这种逻辑上的混乱.尤其可怕的是，如果这种错误发生了，则无论自己怎样检查，也很难发现这个错误.

例5（A）若函数f（x）＝x3+（a+1）x2+3ax+2（a是常数，a∈R）在x∈[1，2]时的最大值是f（1），则a的取值范围是__________________.

（B）若函数f（x）＝x3+（a+1）x2+3ax+2（a是常数，a∈R）在x∈[1，2]时的最大值是f（2），则a的取值范围是___________________.

解（A）由图3可见，即解得.

（B）错解令这是仿照（A）给出的.但是，这个条件只给出了一种可能性.在此可能性之下固然“可以”导致f（2）取得最大值，却不能“保证”它取得最大值（图4）.因此，这种解法是错误的.

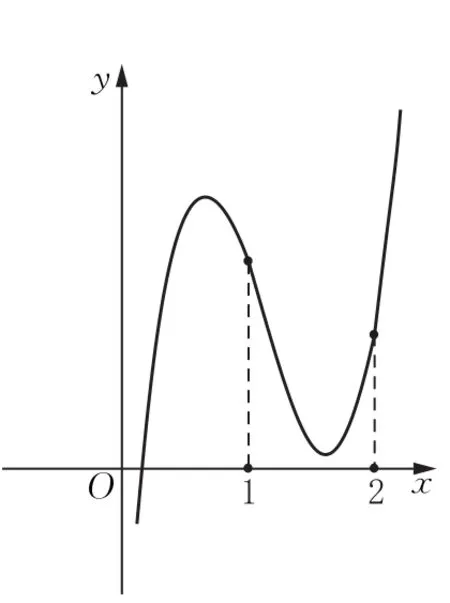
图3

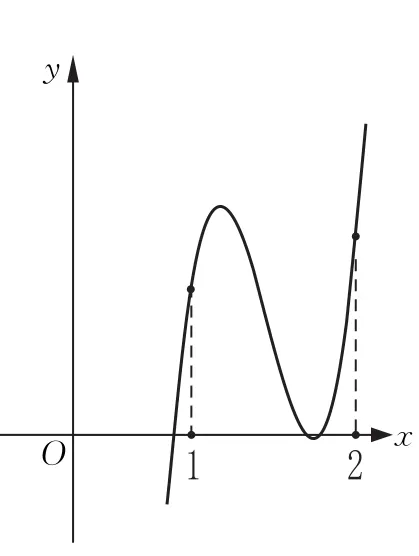
图4

正解在x∈[1，2]时的最大值是f（2），故∀x∈[1，2]，恒有f（2）≥f（x），即23+（a+1）22+6a+2≥x3+，即令，故.

结语

数学是一门非常严谨的学科，每个术语或名词的含义都是非常明确的，必须能进行清晰的辨别.特别是对于有相似性的名词，比如极大值和最大值，公约数和公倍数、中线和中位线，一定不能满足于“有印象”或“一知半解”.另外，对一些变式的说法也应当根据语言的逻辑意义准确把握.