平面向量学习偶得
丁 昀
转眼间高中前两年就过去了,如今我已是一名高三学生了.老师在课上经常讲一些问题的解题技巧,部分同学听了以后就去疯狂刷题,但收效甚微,忘了老师指导我们不能只顾埋头拉车,更要抬头看路,即使记得的同学,对具体怎么看路,也表示很迷茫.
在高中数学学习中,我还没有经历过疯狂刷题的阶段,因为我总想着能否尽量少刷题,也能取得较好的成绩.琢磨多了以后,我对老师常说的高考核心知识点的解题方法有了一些想法.利用暑假时间我定下心来整理了部分问题,别说,还真有豁然开朗的感觉.下面就以平面向量的部分问题来谈谈我的感受.
在平面向量问题中,我们经常要用到基底化方法和坐标化方法,但仅仅知道这些是不够的.
例1在△ABD中,AB=2,AD=,E,C分别在线段AD,BD上,且AE=,则∠A=_________.
解析根据平面向量基本定理,平面内任一向量都可以用一对不共线的向量(基底)来线性表示,利用基底进行运算,即“基底化”,这是我们解决向量问题的“看家本领”.


图1

学习体会:用“基底化”方法解决向量问题,也就是老师上课时经常挂在嘴边的“通法”.根据图形结构,选择合适的基底,直接影响到后续问题计算量的大小,千万不可“乱点鸳鸯谱”,基底的选择体现了我们对问题本质的理解.我的经验是,基底一般选择长度已知的向量、互相垂直的向量或者夹角已知的向量,再把问题中的相关向量用基底表示出来.
例2在矩形ABCD中,,BC=2,点E为BC的中点,点F在边CD上,若,则的值为________.
解析在该问题中,由于点F的确切位置一开始不明确,我考虑从反过来确定点F的确切位置.平面向量可用基底表示,还可以用坐标表示,由于坐标运算的简便性,“坐标化”也是解决向量问题的最基本方法.
考虑到矩形ABCD的条件,以A为坐标原点,AB为x轴建立平面直角坐标系,写出各个需要的点的坐标,解决起来就妥妥的了.
以A为坐标原点,AB为x轴建立平面直角坐标系,

图2
学习体会:在整理的过程中,我发现一般只要题目条件中出现了垂直结构,那么不管是求数量积还是其他相关问题,建立直角坐标系后,坐标化解决问题往往比较顺利!在建系的策略上,当图形为矩形、等腰三角形、圆等具有对称结构时可以优先考虑建系.
例3将函数y=f(x)的图象按向量平移后得到函数y=的图象,求函数y=f(x)的解析式.
解析按向量平移表示的含义是函数y=f(x)的图象向左平移个单位长度,向下平移2个单位长度得到的图象.
将原有平移过程反过来,函数y=中的x用“”替换,再将函数值增加2可得到函数y=f(x)的解析式,即2=sinx.
学习体会:函数图象平移应用广泛,而沿向量平移后许多函数可以得到化简的功效,虽然两者是相通的,但我和我的小伙伴们经常傻傻地将两者混为一谈.这个问题本身不是什么难题,但的确困扰了我好长时间,所以印象特别深刻.在理解向量平移的意义后,不妨将向量平移问题转化为图象平移问题,更容易掌握.后来我慢慢体会到,像这类在知识点交叉的问题,厘清概念的本质就显得尤为重要,这是单纯的刷题难以做到的.
你还别说,有了刚才几个问题的整理过程,我对向量问题的处理一下子自信了许多,下面来看一道思考题.
思考题如图所示,AB是圆O的直径,P是圆弧AB上的一点,M,N是直径上关于O对称的两点,且AB=6,M N=4,则=________.

图3
你会用几种方法解这道题呢?
我想到了几种方法,跟大家分享一下:


图4

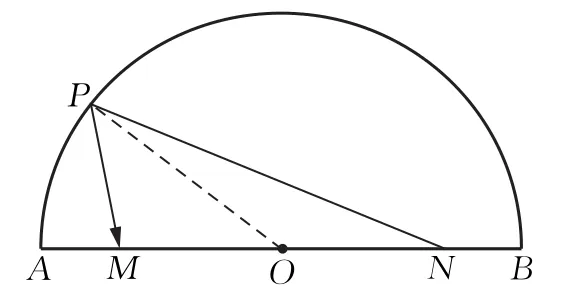
图5
方法3以O为原点建立直角坐标系,设P(x,y),则,,且点P所在的圆O的方程为,.
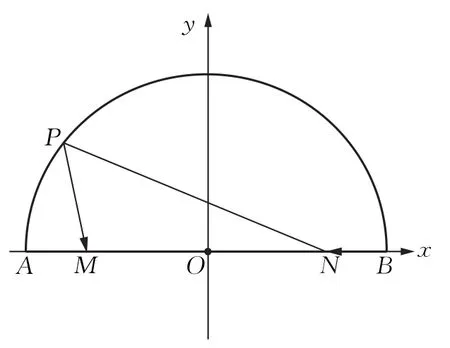
图6
方法4将点P运动到圆弧中点(特殊化),然后求,计算方法:
以O为原点建立直角坐标系,则P(0,3),,
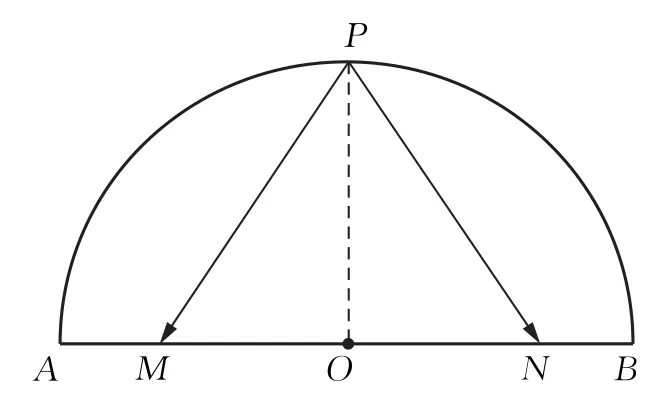
图7
学习体会:方法1和方法2是利用平面内的同一组基底来求解,从不同基底方案的选择中,我们可以体会到合理选择基底的重要性.方法3是通过建立坐标系解决问题的,不同建系方案就不再比较了,相信大家都可以轻松搞定.一般来说,对于特殊的图形往往用坐标化的方法更加简捷有效.方法4可以说是跳出了前面常规思路的限制,特殊化后,秒杀问题,体现出思考后的智慧化解题策略.
王国维在《人间词话》中说:“诗人对宇宙人生,须入乎其内,又须出乎其外.入乎其内,故能写之.出乎其外,故能观之.入乎其内,故有生气.出乎其外,故有高致.”数学学习需要有思考和反思能力,更需要具备举一反三、触类旁通的灵动性,不然就会迷失在茫茫题海中难以自拔.

