例谈如何结合图形判定二面角的平面角

江荣芬

求二面角的平面角是立体几何学习中的重点，也是高考的热点之一.解题时可以先求两个平面的法向量所成的角，由于一个平面的法向量不唯一，长度不等且有两个方向，二面角的平面角范围是0≤θ≤π.二面角的大小与其两个面的法向量所成的角是“相等”还是“互补”成为难点和关键，本文拟给出一个简单的判断方法.

先来分析一下二面角与两个法向量n1，n2所成角的关系，以便突破上述难点：

已知二面角α-l-β，在二面角内任取一点P，过点P作PA⊥α，PB⊥β，垂足分别为A，B，则l⊥平面PAB，设l∩平面PAB于点O，连结OA，OB，则OA⊥l，OB⊥l，记∠AOB＝θ，所以θ为二面角α-l-β的平面角.平面α的一个法向量为n1，平面β的一个法向量为n2，将这两个法向量的起点均移至点P，当两个法向量同时指向平面或者同时远离平面（如图1，图2），则二面角的平面角θ与两个法向量n1，n2所成的角〈n1，n2〉互补，即θ＝π- 〈n1，n2〉，概括为“同向互补”；

将这两个法向量的起点均移至点P，当两个法向量一个指向平面，另一个远离平面（如图3，图4），则二面角的平面角θ与两个法向量n1，n2所成的角〈n1，n2〉相等，即θ＝〈n1，n2〉，概括为“异向相同”.

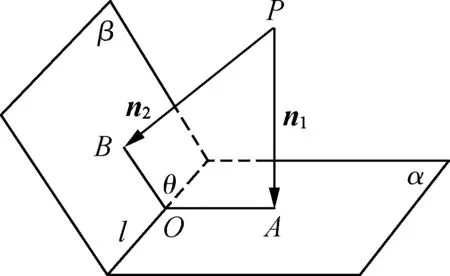
图1

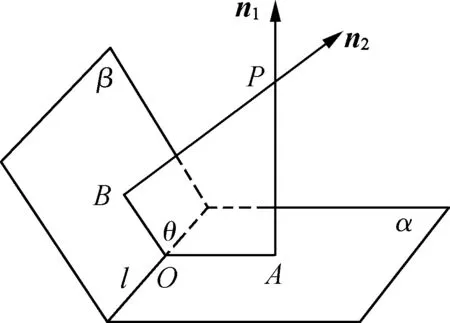
图2

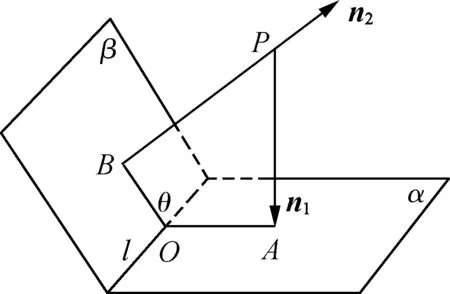
图3

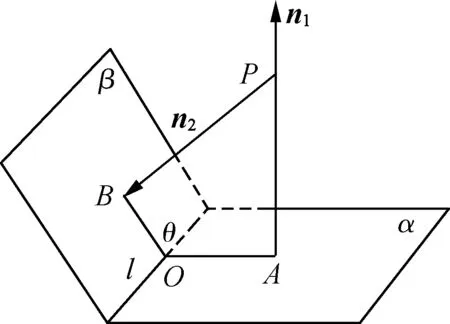
图4

理清了概念，我们再来看两道例题：

例1如图5，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，AB⊥B1C.

（1）证明：AC＝AB1；

（2）若AC⊥AB1，∠CBB1＝60°，AB＝BC，求二面角的余弦值.

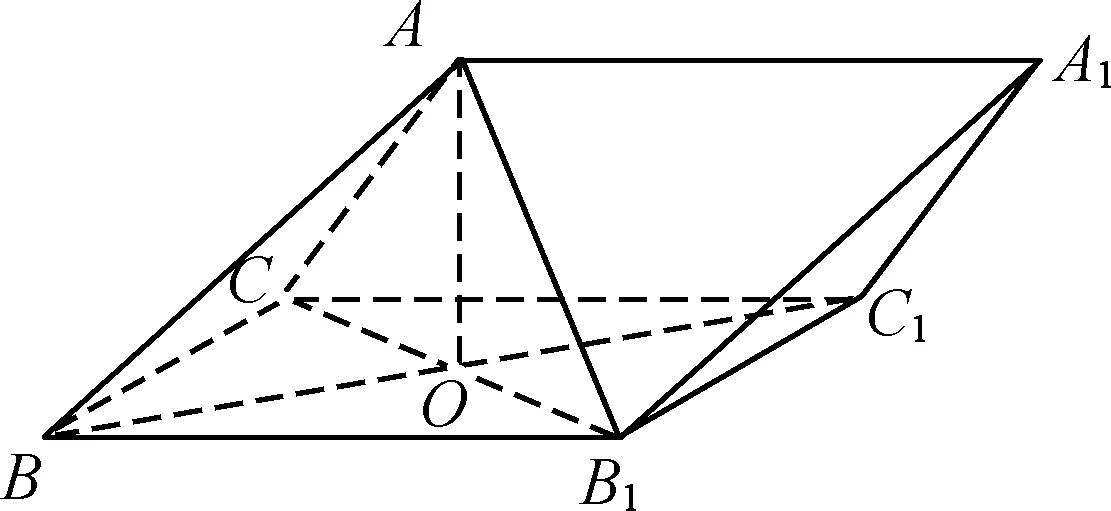
图5

解析（1）略.（2）因为AC⊥AB1，AC＝AB1，O为B1C的中点，所以AO＝CO.又因为AB＝BC，所 以 △BOA≌△BOC，所以OA⊥OB，从而OA，OB，OB1两两互相垂直.以为正交基底，建立如图6所示的空间直角坐标系O-x yz，不妨设，则.因为∠CBB1＝60°，所以△CBB1为正三角形，则，故B1（0，1，0），A（0，0，1），.设平面AB1A1的一个法向量为n1＝（x1，y1，z1），则所以

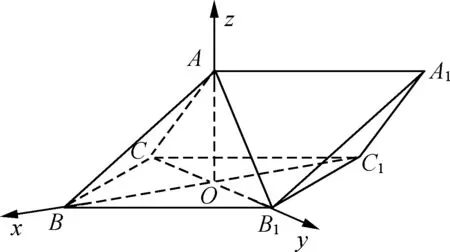
图6

不妨令x1＝1，则，所以平面AB1A1的一个法向量为.

点评二面角的平面角求法：第一步分别求出两个平面的法向量；第二步计算这两个法向量所成的角的余弦值；第三步借助具体的图形判断二面角的平面角与两个法向量所成的角是相等还是互补关系，然后得出结论，这一步始终困扰着大家.先将向量n1＝起点放在坐标系原点O，观察向量n1的方向，再将其起点移至二面角内的任意一点，判断得向量n1指向平面AB1A1，按同样的方法判断得向量n2远离平面A1B1C1，故二面角C1的平面角与两个法向量n1，n2所成的角相等.

例2如图7，四棱锥P-ABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，，M为BC上一点，且.

（1）求PO的长；

（2）求二面角A-PM-C的余弦值.

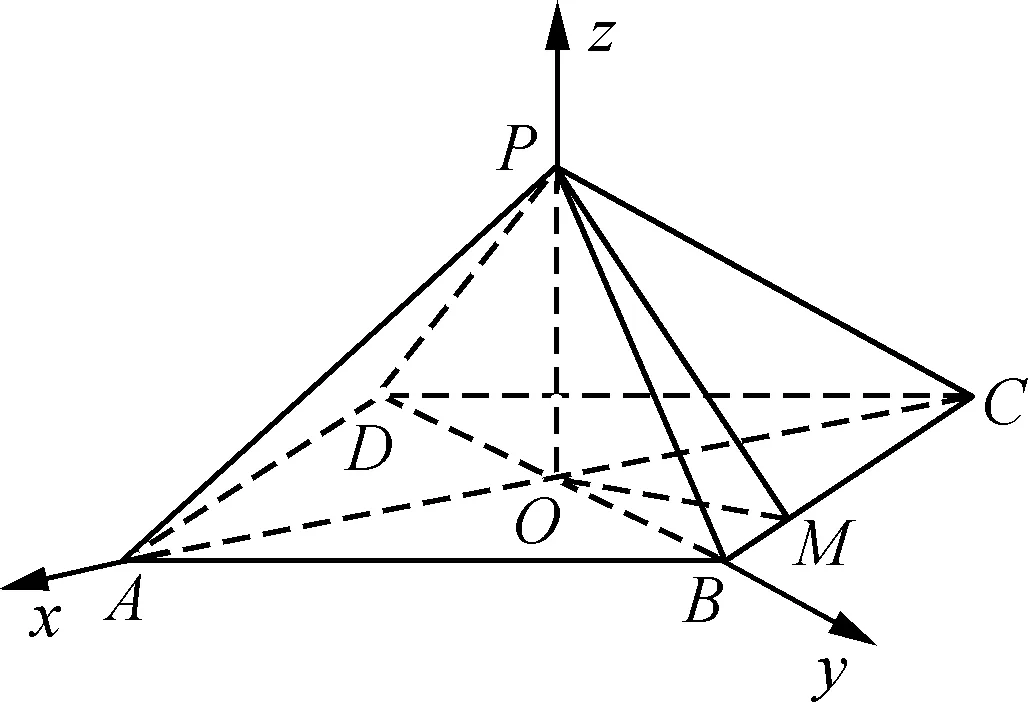
图7

解析连结AC，BD，OM，因为四边形ABCD是以O为中心的菱形，则AC∩BD＝O，且AC⊥BD.以O为坐标原点，为正交基底，建立如图7所示的空间直角坐标系O-xyz，因为∠BAD＝，所以，所以.由题意知，所以设P（0，0，a），a＞0，则.因 为MP⊥AP，故，所以，由a＞0得a＝，即PO的长为.

点评将向量起点放在坐标系原点O（原点O也为二面角APM-C内的一点）观察向量n1的方向，判断得向量n1指向平面AMP，按同样的方法判断得向量n2也指向平面PMC，故二面角APM-C的平面角与两法向量n1，n2所成的角〈n1，n2〉互补.