老师，我怎么学会思考——导数篇

王思俭

经常有同学这样议论：

老师，平时常规的题目我会做，如不含参数的导数问题中求极值、单调区间、最值等，但遇到含有参数的导数题，我就不知道该怎样思考了；

我对求含参数的闭区间上的最大值与最小值，不知道如何思考；

证明函数中的不等式问题，往往到中间某一步不知道如何思考下去；

我对函数综合题不知道怎样思考；

……

针对这些质疑，我邀请几位学生就“导数的应用”进行交流，旨在引导学生学会思考，而不是拼命刷题，指导他们做中悟道，学会体验数学.

生甲：（2018年江苏卷第12题）若函数f（x）＝2x3-ax2+1（a∈R）在（0，+∞）内有且只有一个零点，则f（x）在[-1，1]上的最大值与最小值的和为________.

我也知道要先求出a，然后再求最值，但是“函数有且只有一个零点”该怎么思考呢？我在这一处卡住了.

教师：首先我们利用导数研究函数单调性、极值等问题，其次考虑函数在（0，+∞）上的极值与函数有且只有一个零点的关系，最后再求最值，你再试试看.

生甲：我想到了，只要求出f（x）在（0，+∞）上的极大值或极小值为零，函数在（0，+∞）上就只有唯一零点了.f′（x）＝6x2-2ax，讨论当a≤0时，f（x）在（0，+∞）上单调递增，而f（0）＝1，因此f（x）在（0，+∞）上无零点.当a＞0时，可以讨论得f（x）在处有极小值，于是有由题意知，，即a＝3.所以f（x）＝2x3-3x2+1.又因为f（-1）＝-4，f（1）＝0，f（0）＝1.因此，当x∈ [-1，1]时，f（x）max＝1，f（x）min＝-4，故最大值与最小值之和为-3.

生乙：在求最大值与最小值时，应该先列表讨论单调性，指出极值，最后再求最值.

教师：很好！一定要注意解题的规范性.请看变题1：

已知函数f（x）＝2x3-3x2+1，求当x∈ [0，t]（其中t＞0为常数）时，f（x）的最大值.

生乙：根据刚才的结论，f（x）在（0，1）上单调递减，在（1，+∞）上单调递增，当0＜t≤2时，最大值为f（0）＝1；当t＞2时，最大值为f（t）＝2t3-3t2+1.

教师：你为什么用2作为一个分界点？

生乙：根据函数对称性，x＝2是其对称轴.

生丙：这是三次函数，怎么会有对称轴呢？应该讨论极值点x＝1在区间[0，t]右侧，和在区间[0，t]内，但是这种情况不知道怎么思考了.

生丁：因为极大值f（0）＝1，因此要寻找f（x0）＝1时非零x0的值，解方程得.当时，f（x）的最大值为f（0）＝1；当时，f（x）的最大值为f（t）＝2t3-3t2+1.

生戊：根据f（x）在（0，1）上单调递减，在（1，+∞）上单调递增，因此，f（x）的最大值应该在两个端点取到，于是只要比较两个端点的函数值大小即可，即f（t）-f（0）＝于是分类讨论得出结论.

教师：很好！他先给出函数的单调区间，从而只需比较两个端点的函数值大小即可.变题1是一个端点固定，另一个端点在变化，如果两个端点都在变，又应该如何处理呢？请看变题2：

已知函数f（x）＝2x3-3x2+1（x∈[t，t+1]），记f（x）的最大值与最小值的差为G（t），求G（t）的函数解析式.

生甲：单纯利用生戊的方法无法求解，那应该怎样思考呢？

教师：根据三次函数图象的变化趋势，结合给定区间[t，t+1]，先讨论极值点是否在区间内，再比较大小.

生乙：应该将区间端点与极值点的大小进行比较，将此区间从极值点x＝0的左侧向右移动，再进行分类讨论.当t+1≤0，即t≤-1时，f（x）在[t，t+1]上单调递增，因此f（x）max＝f（t+1），f（x）min＝f（t），所以G（t）＝f（t+1）-f（t）＝6t2-1.同理，当t≥1时，f（x）在[t，t+1]上单调递增，因此f（x）max＝f（t+1），f（x）min＝f（t），所以G（t）＝f（t+1）-f（t）＝6t2-1.当-1＜t＜1时，f（x）max＝1，f（x）min＝0，所以G（x）＝1.

生丙：当-1＜t＜1时，还应该再分极大值点在区间内和极小值点在区间内两种情况.当t+1＞0且t≤0，即-1＜t≤0时，f（x）max＝f（0），f（x）min＝min｛f（t），f（t+1）｝.又因为f（t+1）-f（t）＝6t2-1，所以，当时，f（x）min＝f（t+1），故G（t）＝f（0）-f（t+1）＝-2t3-3t2+1；当时，f（x）min＝f（t），故G（t）＝-2t3+3t2.由对称性，同理可得，当时，G（t）＝2t3+3t2-1；当时，G（t）＝2t3-3t2.

生丁：你的结论也是错的，不能由对称性得出，因为，当0＜t＜1时，f（x）min＝f（1）＝0，f（x）max＝max｛f（t），f（t+1）｝，因此当时，f（x）max＝f（t），即；当时，f（x）max＝f（t+1），即G（t）＝2t3+3t2.综上所述，

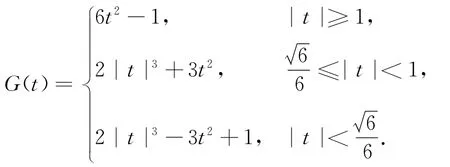
教师：很好！分段函数中可以合并的尽量合并，减少分类的层次，简洁明了.本题分类层次较多，但最后还是可以合并的，先分后合.再看变题3：

已知函数f（x）＝2x3-ax2+1（a＞0），若不等式｜f（x1）-f（x2）｜≥｜lnx1-lnx2｜对任意x1，x2∈[a，+∞）恒成立，求实数a的取值范围.

生甲：这是二元变量的不等式恒成立问题，的确不会思考了.

教师：你们想一想，能否把二元的问题等价转化为一元问题？你们能否想办法将x1，x2分别转移在不等式两侧？

生甲：分类讨论思想，去掉绝对值，移项后，两边代数式的结构不一定相同，怎么办？

教师：分类讨论确实太烦琐了，能否避免分类呢？首先，你们要研究函数f（x）的单调性；其次，由于x1，x2是任意的，于是可以不妨设x1＜x2，这样是否可以了？

生乙：我就是这样想的，由原题知，f（x）在[a，+∞）上单调递增，不妨设x1＜x2，于是有f（x1）＜f（x2），而lnx1＜lnx2，因此不等式等价转化为，即，再转化为，接下来该怎么思考呢？

教师：你们观察不等式两侧的结构是否相同？

生丙：构造函数F（x）＝2x3-ax2+1-lnx，不等式再次转化为F（x1）＜F（x2）.由于x1＜x2，因此函数F（x）在[a，+∞）上单调递增，即0，分离参变量法求解，好像有点困难！

生丁：可以等价转化为6x3-2ax2-1≥0对一切x∈ [a，+∞）恒成立，设h（x）＝6x3-2ax2-1，h′（x）＝18x2-，因此h（x）在[a，+∞）上单调递增，所以h（x）min＝h（a）＝4a3-1.因为对一切x∈ [a，+∞）都有h（x）≥0成立，因此h（x）min≥0，即4a3-1≥0，所以.所以当时，原不等式成立.

教师：很好！经过大家共同努力，此题终于圆满解决了.本题的思考过程请大家再回顾一下，梳理一下，遇到这类题该怎样考虑，如何转化.

生丙：（2018年全国卷一第21题）已知函数.

（1）讨论函数f（x）的单调性；

（2）若f（x）存在两个极小值x1，x2，证明：.

第（1）小题求导后，f′（x） ＝，对于x2-ax+1的判别式Δ＝a2-4≤0，即-2≤a≤2时，f（x）在（0，+∞）单调递减；当a＞2或a＜-2时，，讨论得，函数f（x）在（0，x1），（x2，+∞）上单调递减，在（x1，x2）上单调递增.而第（2）小题怎么思考呢？

生丁：第二种情况结论错了，a＜-2时，x1＜0，x2＜0，不合适，舍去.当a＞2时，根据x1x2＝1，有0＜x1＜1＜x2，因此，函数f（x）在（0，x1），（x2，+∞）上单调递减，在（x1，x2）上单调递增.于是x1是极小值点，x2是极大值点.而第（2）题转化为，要证明原不等式成立，只要证明1，下面我不会做了，该怎么思考呢？

教师：你们能否再进一步转化，转化为一个变量的不等式呢？

生戊：根据等价于，构造函数，于是有在（1，+∞）上单调递增，因此g（x）＞g（1）＝0.所以，即.故.

教师：经过几位同学的共同努力，终于圆满解决了这道高考压轴题.从这道题的求解过程可以看出，同学们的思考过程中经常遇到障碍，如何突破障碍是关键.同学们要在障碍处，尽量找出思维受阻的症结在哪里；再观察题目的条件和结论以及中间结论，比较一下中间的结论与最终的结论还差多远；然后再将一些信息重新组合，再思考、再理解，再实践，多重复几次思考再思考，问题一定会得到解决.

实战演练

（1）讨论函数f（x）的单调性；

（2）若f（x）存在两个极值x1，x2，证明：.

参考答案