准确理解“极值”
陈水青
导数在高中数学中是一个很重要的知识点,在高考中有关导数的解答题常考常新,利用导数研究函数的单调性与极值是解决函数问题的重要方法.笔者在教学过程中发现很多同学在解决极值问题时,因对极值的概念理解不透而导致解题错误.
一、认清本质
极值是函数的局部性质,是函数在某点处的值与其附近“左、右”函数值比较的结果.
图1中f(x1)比左、右侧很小范围内的函数值都大,故f(x1)是一个极大值;上图中f(x2)比左、右侧很小范围内的函数值都小,故f(x2)是一个极小值.同样,f(x3)、f(x4)分别是函数f(x)的极大值、极小值.但是f(a)与f(b)不是极值,因为它们不是与其附近“左、右”函数值比较的结果.
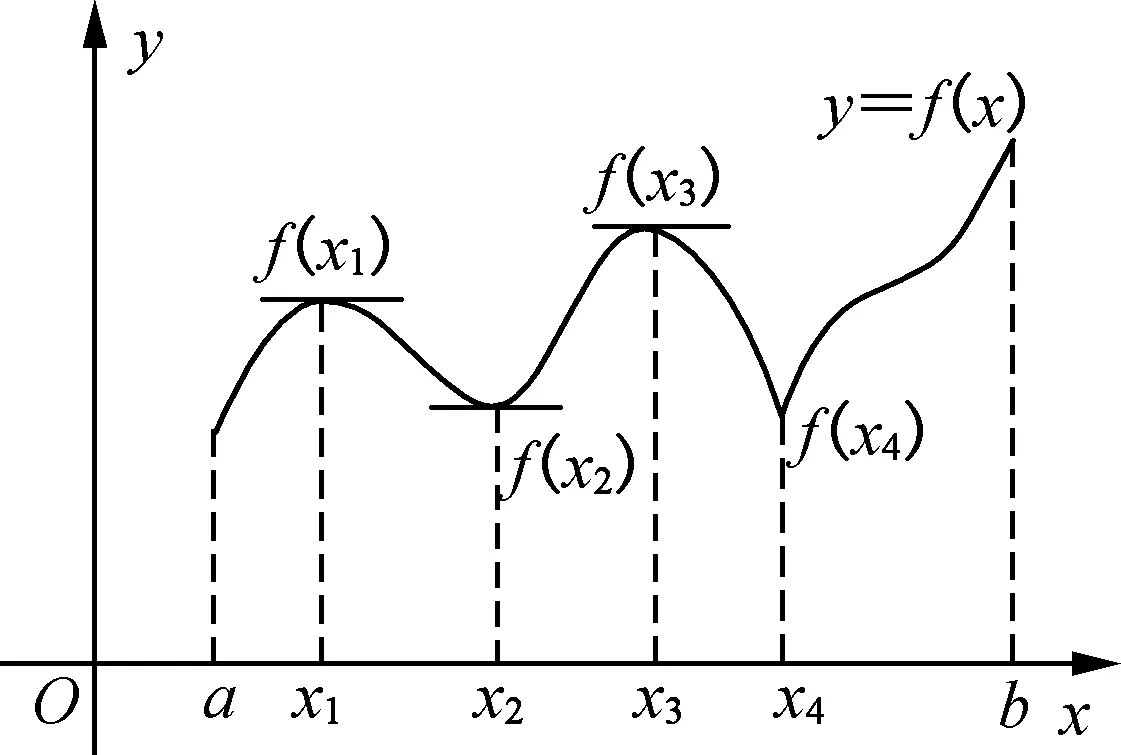
图1
二、走出误区
问题:函数f(x)=x3+1,其导函数f′(x)=3x2,显然f′(0)=0,那么f(0)是f(x)的极值吗?
f(x)是 R上的增函数,f(x)在“0”的左侧单调增、在“0”的右侧还是单调增,f(0)比左侧很小范围内的函数值都大,但是同右侧相比,则要小,故f(0)不是极大值;同样,f(0)也不是极小值.
实际上,f′(0)=0只是反映出在“0”的瞬时变化率为“0”(从图象上可以看出上升速度先是越来越慢,然后又越来越快).可见,若f′(x0)=0,x0未必是极值点.
三、实例分析
例函数f(x)=x3+ax2+bx+a2在x=1处有极值10,求实数a,b的值.
错解f′(x)=3x2+2ax+b,由题意知f′(1)=0,且f(1)=10,即2a+b+3=0,且a2+a+b+1=10,解得a=4,b=-11或a=-3,b=3.
剖析错解中认为f(x0)为极值的充要条件是f′(x0)=0,实际上f(x0)为极值的充要条件是f′(x0)=0且x0附近两侧的单调性相反,所以应对求出的结果进行验证:
当a=4,b=-11时f′(x)=3x2+8x-11=(3x+11)(x-1).
在x=1附近两侧的符号相反,即单调性相反(如图2(1)).
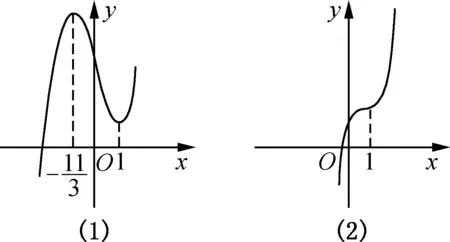
图2
所以a=4,b=-11满足题意.
当a= -3,b=3 时,f′(x)=3(x-1)2.
在x=1附近两侧的符号相同,即单调性一致(如图2(2)),f(1)不是极值.
不符题意,舍去.
所以a=4,b=-11.
四、经验总结
1.若f′(x0)=0,f(x0)未必是极值;f(x0)是否是极值,取决于x0左、右两侧的单调性是否相反,解题时要注意检验其左、右两侧的导数符号是否相反.若f′(x0)≠0,则在x=x0处肯定没有极值.
2.极值是函数的局部性质,是函数在某点处的值与其附近“左、右”函数值比较的结果,极值点不可能出现在区间(不论开区间还是闭区间)端点处.
3.极值与最值联系紧密,但也要注意其区别.例如求函数f(x)=x3+4x2-11x+16在[0,3]上的最值.据图2(1)可以看出,在区间[0,3]上,实际上只有一个极值点,且为极小值,故在[0,3]上的最小值就是极小值10,而最大值则是f(0)与f(3)的比较.在注意与区间端点处的函数值比较的同时,也是灵活地根据图象,避免无效的计算,如本题计算最小值时,便不用将f(1)=10与f(0),f(3)比较.但若将区间扩大至[-2,3],便需要全面比较了.灵活运用,方为正道.
4.要注意转化.有些题目看起来与极值无关,实际上则由极值把关最关键处.如:已知函数f(x)=x3+ax2+x+1,若要f(x)的图象与x轴有且只有一个交点,求a的取值范围.由f′(x)=3x2+2ax+1知,导函数图象开口向上,若Δ≤0,则原函数图象如图2(2),符合题意;若Δ≥0,观察图2(1),则需极小值大于0或极大值小于0即可.

