图形数探秘

李 红

数学的发展离不开数，我们对于数学最初、最直观的认识就是数字.古希腊数学家毕达哥拉斯认为“万物皆数”（由于历史条件的限制，这里的数当时是指有理数），毕达哥拉斯学派研究数时，喜欢用沙滩上的小石子摆成不同的几何图形，于是就产生了一系列的图形数.

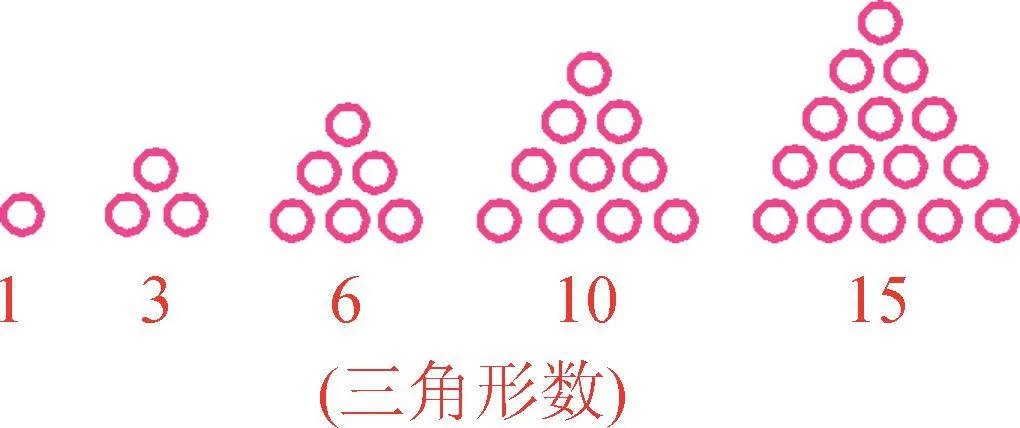
图1

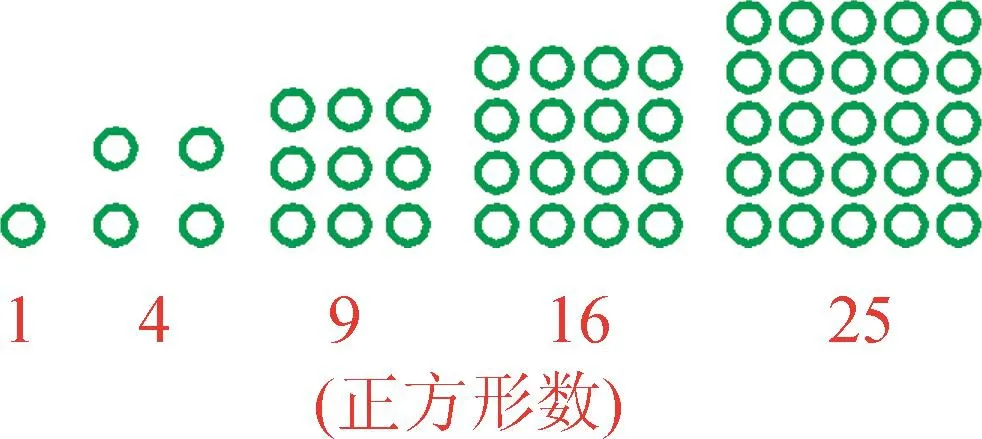
图2

毕达哥拉斯发现，当小石子的数目是1，3，6，10，15，…时，小石子都能摆成正三角形，他把这些数叫做“三角形数”（如图1）；当小石子的数目是1，4，9，16，25，…时，都能摆成正方形，这些数叫做“正方形数”（如图2）.以此类推，还有长方形数、梯形数、五边形数、六边形数等等.

仔细观察上面的图形，不难发现图形数有着很多有趣的规律：

三角形数是从1开始的一些连续自然数的和，如

正方形数是自然数n的平方n2，如

任意两个相邻的三角形数之和都是正方形数，如

古希腊人不仅研究了把点排列在平面上的图形数，而且将其升级到了空间.如果把三角形数1，3，6，10，15，21，28，36，45，55，66，…“一层一层摞起来”，就可以形成“三棱锥数”1，4，10，20，35，56，84，120，…（如图3）；同样，如果把正方形数1，4，9，16，25，36，49，64，81，100，…“一层一层摞起来”，就可以形成“四棱锥数”1，5，14，30，55，91，140，204，…（如图3）.其中已经体现出我们数列学习中的“数列求和”的韵味了.

图3

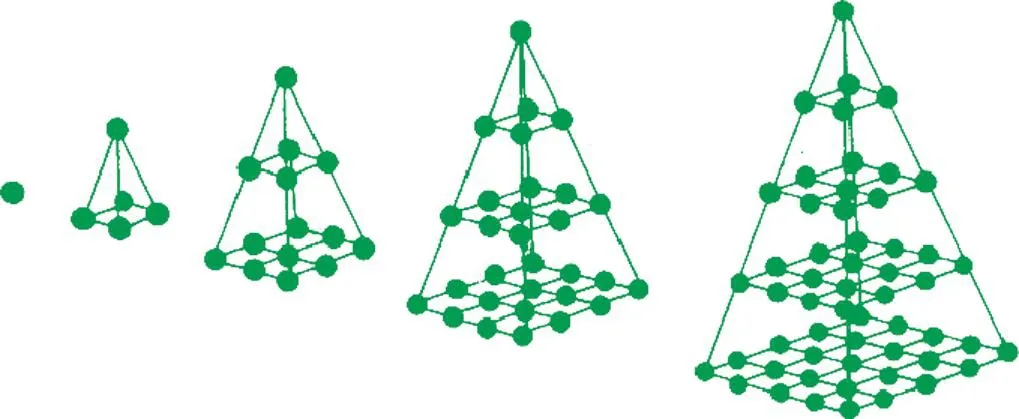
图4

图形数把抽象的数与直观的图形巧妙地联系起来，真是集数形宠爱于一身呀！利用这个特点可以推出许多重要公式.把1，4，9，16，25这5个连续的正方形数稍加变形，排成如图5的“摩天楼形数”.如果在它的两侧各加上同样的5个连续的正方形数，就会得到一个如图6的“长方形数”.

图5

图6

推而广之，就得到n个连续平方数的和的公式：.

图形数用其生动直观的图形，替代了烦琐的计算，演绎出许多重要公式，真是不可思议！我国古代著名数学家杨辉也曾用独特的“中国式图形数”方法得出了这个公式.下面，就让我们重温一下他的方法：

取3份12，22，32，…，n2个小立方体，分别把它们组成A，B，C三个阶梯状的四角锥形，再把它们拼成如D的模样（如图7，以n＝4为例）：

图7

然后，把最上面突出的一层小立方体，从水平方向一半的位置横切一刀，则每个突出的小立方体都被一分为二，再凹凸相对合在一起，正好铺满层，于是得到一个长方体.这个长方体长n+1、宽n，而高等于，体积是

因为这个立方体是由3份12，22，32，…，n2个小立方体拼成的，所以，于是得到连续平方数的和的公式：12+22+32+…+n2＝.这与古希腊人用图形数法得到的公式是一致的.杨辉所用的方法，更直观、更容易理解，真称得上是精彩绝伦！

我们用数形结合与合情推理的方法，妙趣横生地得到了重要的公式，小伙伴们是不是“惊艳”于图形数的神奇呢？图形数的魅力，妙不可言！