视角发散，价值多元——以平面向量数量积问题为例

晋 杰

平面向量数量积是向量知识的重要内容，也是高考的热点问题.我们在解决平面向量数量积问题时一般采用的方法是基底法或解析法.把握好问题的本质，快速、准确地解决平面向量问题，达到“事半功倍”的效果，这是我们每一个同学学习数学努力的方向.下面我们就以一道高三模拟考试中出现的考题为例，剖析如何在多元视角下处理好一类平面向量数量积问题.

试题呈现

如图1，在平面四边形ABCD中，AB＝2，△BCD是等边三角形，若，则AD的长为________.

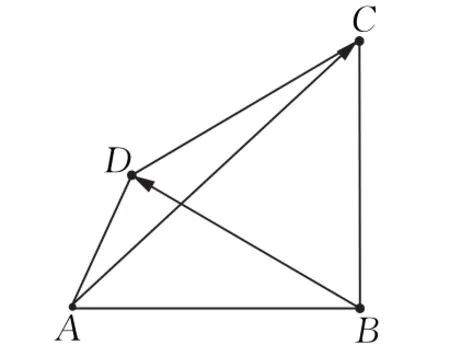
图1

试题分析应用平面向量的数量积解决平面几何问题，是高考的热点问题.本题中是以四边形和三角形为基本图形背景，数量积为题眼（核心条件）.如何处理好这个数量积是我们首先需要思考的问题.对于数量积的处理，我们通常从两个角度考虑：①基底法，抓住向量的模和夹角的关系；②解析法，将向量坐标化以后再进行数量积运算.若采用角度①，直接将转化为模与夹角的关系，则无法发现与所求边长AD的关系，因此选择恰当的基底，将数量积中的部分（或全部）向量分解，架起已知量与未知量之间的“桥梁”，势在必行.那么如何选择基底？分解还是，抑或是两个向量都分解，值得我们好好推敲.若采用角度②，如何合理地建立坐标系也是个大问题.

下面尝试从多个视角剖析这个问题，希望对读者有所启发.

视角一由于AD是四边形的一条边，故可选取四边形的相邻两边为基底，把对角线所在向量问题转化到所求模长的向量上来.同时准确地运用向量数量积的定义，找准向量的夹角，以及余弦定理的应用是解决本题的关键.

将上面的两个结论以及等边△BCD中DC＝BC，AB＝2均代入（＊）式，

即可求出AD的长度.

视角二整体代换，优化解题，化繁为简.这需要同学们在解题时，细心观察，理清思路，不能急于求成.

视角三利用平面图形的特征，因为AB与AD都集中在△ABD中，若取线段BD的中点M，连结AM，则，而，即以为基底分别将分解，至此AB（已知）与AD（所求）建立了联系，但还缺少“桥梁”（方程），而就是一个方程，此时我们只需将也用为基底分解即可.不难发现，而 △BCD为等边三角形，恰巧CM⊥BD，则，问题得到圆满解决.

解析取线段BD的中点M，连结AM，CM.

图2

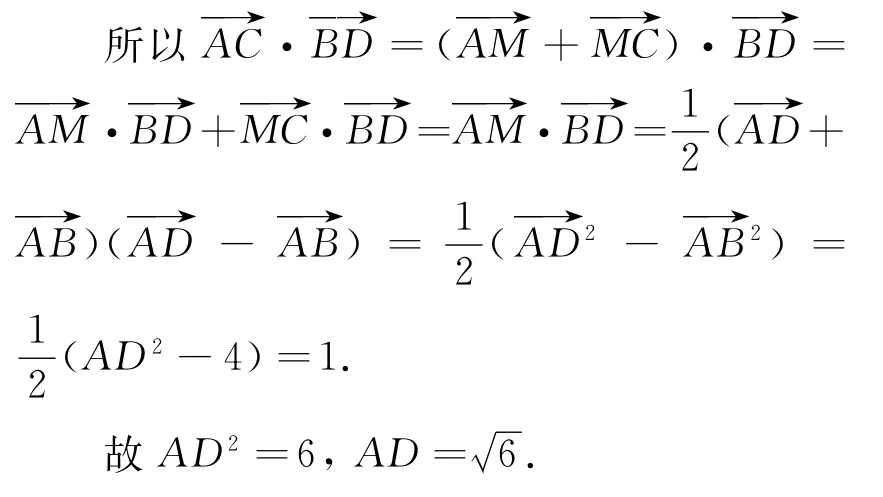
视角四采用解析法时，如何合理建系是我们首先需要反复权衡的问题.我们可以抓住等边三角形的图形特征，合理建系、设点.虽然解题中会出现多元变量，但是整体代入的思想和方程思想的渗透，以及设而不求的解题方法的灵活运用，最终达到消元的目的.

解析等边三角形建系（如图3，可以把图形适当旋转），引入A（m，n），B（t，0），D（-t，0）这三个点坐标，易求得C（0，，于是得到下 面的解 法：，所以2tm＝1①.又因为，所以②.

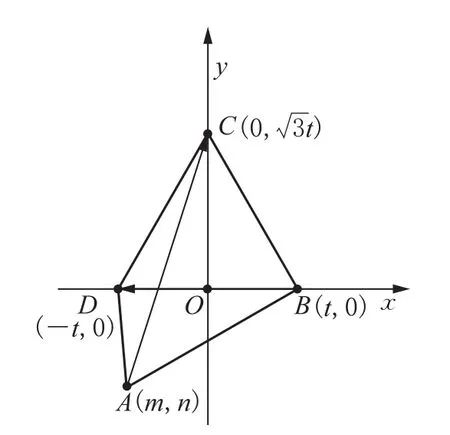
图3

视角五利用“四点向量定理”：平面四边形ABCD中，，快速解题.该定理的证明过程可以参考视角一的路径②，有兴趣的同学可以自己尝试证明，这里不再赘述.

解析由“四点向量定理”，得，又因为△BCD是等边三角形，BC＝DC，故，得解.

解题感悟在处理平面向量数量积的有关问题时，基底法和解析法是两种基本方法.视角一从定义出发，上手虽容易，但在求cosθ时容易卡壳，考试时不易深入，但平时学习，如能继续探究，虽然有些繁，但若将平面向量和解三角形相结合，对高三复习的知识融合一定有所帮助.视角二是对视角一的有力补充，降低了视角一的运算量，但对学生的观察能力和信息的整合能力有较高的要求.视角三“以巧拨千斤”，首先要对平面向量的几何运算熟悉，就能有效解决此问题，这是解决此类问题的通性通法.视角四通过建系，借助向量的坐标表示，成功将几何问题变成了代数问题，体现了平面向量的代数表征.视角五，独辟蹊径，抓住四边形对角线数量积与四边的关系，巧用“四点向量定理”，拓宽了学生的知识面.上面五种不同的视角体现了平面向量“数与形”的特征.

高考与平时学习并不完全是同一回事.高考注重解题时效，即在最短时间内准确地解决问题.而我们在平时的学习中要善于通过分析，多角度思考，纵横联系，充分暴露思维的过程，从而达到优化解题的目的，找到最优解，价值多元.同学们在平时要能坚持这样做下去，并辅以适当的变式练习，及时归纳、整理、提炼，方能在高考中轻松应对.