不可小觑的渐近线

张春琦

纵观近几年各省高考题，直线与双曲线的关系问题可以说不再是重点，而双曲线几何性质之一的渐近线，其重要性就凸显出来，有必要认真研究.

我们先来欣赏你可能会忽略的、几种常见函数图象的渐近线：

2.正切函数y＝tanx的图象中，x＝是它的渐近线；

原来除双曲线外，还有这么多函数图象有着渐近线.那么研究双曲线的渐进线有哪些作用呢？

一、作图的需要

了解渐近线的定义，会使函数渐近线的学习更为自然、简明，同时解释或证明中学数学所涉及的一些函数图象的渐近线也就有了依据，进而有利于它们的作图.

例如，在双曲线的几何性质中，渐近线是双曲线所特有的性质，过双曲线实轴的两个端点与虚轴的两个端点分别作对称轴的平行线，它们围成一个矩形，其两条对角线所在直线即为双曲线的渐近线.

我们还可以利用渐近线确定双曲线的“张口”大小.

二、数形结合的需要

在解决有关双曲线问题时，需结合渐近线从数形结合上找突破口.

证明设双曲线b＞0），直线，代入得，化简得，仅有一解，即双曲线与直线仅有一个交点.

同时，易证并非切线.

我们首先来看看上个月本杂志的一道例题：

例1已知双曲线与直线y＝kx+1只有一个公共点，则满足条件的直线有几条？

思路将方程与方程y＝kx+1联立方程组，得（1-4k2）x2-8kx-8＝0，再就1-4k2是否为0两种情况进行讨论，得或者，答案为4条.

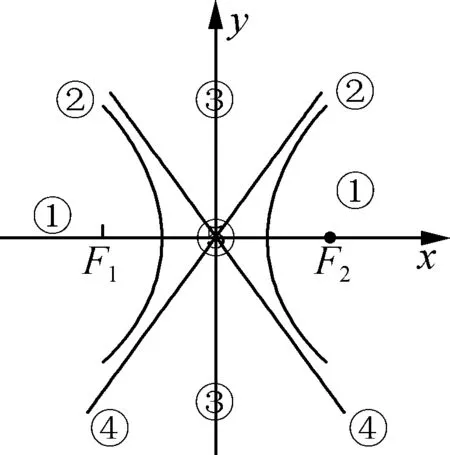
图1

思路2直线y＝kx+1，过 定 点（0，1），可以作出两条分别与渐近线y＝平行以及两条双曲线的切线，一共4条，这样可以避开上面的计算.

问题进一步引申：如图1所示，定点可以分布在5个区域，过定点作直线与双曲线有且仅有一个交点，可以作出的直线数目可能有几种？

区域①：无切线，2条与渐近线平行的直线，合计2条；

区域②：即定点在双曲线上，1条切线，2条与渐近线平行的直线，合计3条；

区域③：2条切线，2条与渐近线平行的直线，合计4条；

区域④：即定点在渐近线上且非原点，1条切线，1条与渐近线平行的直线，合计2条；

区域⑤：即过原点，无切线，无与渐近线平行的直线.

小结：过定点作直线与双曲线有且仅有一个交点，可以作出的直线数目可能有0，2，3，4条.

以上抓住了渐近线与图象的位置的特殊关系，简化了解题，从而达到优化思维的目的.

三、深入研究双曲线性质的需要

例2已知双曲线的两条渐近线方程为x±2y＝0，求此双曲线的离心率.

解设双曲线方程，即，则，即.

证明或者.（或用数形结合证明之）

特别地，等轴双曲线（即实轴和虚轴等长的双曲线），其渐近线方程为x±y＝0，它们互相垂直，且平分双曲线实轴和虚轴所成的角，离心率为.

例3求与双曲线有共同的渐近线，并且过点的双曲线的标准方程.

解与双曲线有共同渐近线的双曲线方程都可以表示的形式.

评注对于双曲线，当t＞0时，所求双曲线的焦点在x轴上，这时其渐近线方程是；当t＜0时，所求双曲线的焦点在y轴上，这时双曲线的标准方程是，其渐近线方程是.

因此，不管t的取值如何，它们的渐近线相同，而将双曲线设为的形式，本质就是设有相同渐近线的双曲线系，再有一个条件（如双曲线的一个点）就可以确定曲线的方程.

限于篇幅，不另外举例，再提供以下三个性质，同学们还可以自己补充有关双曲线渐近线的知识.

1.双曲线上任意一点到两渐近线的距离的乘积是一个常数.

2.从双曲线的一个焦点到一条渐近线的距离等于虚半轴的长b.

四、结束语

渐近线，他像一位正直慈爱的师长，呵护指引着曲线成长的人生轨道，循规蹈矩走向遥远的未来而从不对他强制干涉.

有了渐近线，我们可以较准确地画出曲线的草图；

有了渐近线，双曲线的轨道有了可靠的护栏；

有了渐近线，我们对“曲”、“直”之间存在着这种和谐统一之美，有了更深刻的认识和理解.