在数学课堂教学中培养学生的思维能力

孟维云

摘要：如何在数学课堂上培养学生的思维能力是一个重要课题。初中数学教学高度重视学生思维能力的开发，注重创设教学情境，努力培养学生多角度的思维能力，使学生真正懂得如何学好数学。只有这样，才能更好地适应新课改的需要，培养出会思考、会创新的人才。

关键词：数学课堂;创设情境;培养;多角度思维能力

中图分类号：G633.6   文献标识码：A   文章编号：1992-7711（2018）09-0036

在数学教学中如何发展学生的数学思维，培养学生的思维能力是广泛而值得探讨的课题。培养学生的思维可以从以下几个方面入手：

一、培养学生思维的正确性

思维的正确性，是指学生的思维活动符合逻辑、形成概念正确、判断推理准确。有些学生由于对题目中的某些“字眼”的片面理解，往往导致思维错误。

例如：有这样一道题目：“某种贺年卡大量上市，几天来价格不断下跌。小红第一天买了2张;第二天贺年卡的价格打8折，小红买了5张;第三天贺年卡的价格又下跌了0.2元，小红又买了5张，三天共花了29元。如果用29元在第三天买这种贺年卡，能买多少张？”这道题条件较多，比较复杂，如果审题不清，很容易列错方程;只有把题目理解透彻，弄清每一次的单价关系，才能正确解题。还有，笔者发现初中学生学数学一个很大的盲区，就是定义弄不清楚。例如在学习“对顶角”时，笔者在结合实例的基础上，抽象出它的定义：“如果两个角有公共顶点，并且这两个角的两边互为反向延長线，则这样的两个角称为对顶角。”很快就有学生在问：“老师，什么叫反向延长线？”其实像这样的例子还有很多，所以笔者认为学好数学首先要有正确的概念理解，正确的思维认识，才能有正确的判断推理。另外，在平时教学中，教师要鼓励学生敢于突破常规的思想方法和解题模式，有主见的评价事物，能严格批判自己提出的假设或问题是否正确，善于提出问题和发表不同的看法，训练学生的“质疑”心理，多问几个“为什么”。

二、培养学生思维的灵活性

培养思维的灵活性，要注意引导学生借助已有知识，从不同角度去思考，通过思路发散，激发求异心理，寻找多种解题方法，从中发现最佳解法，从而发展学生的灵活运用能力。我们可以大胆尝试运用开放、民主的教学模式，从教学中充分发挥学生的主体作用，即从学生的生活实际出发，展开学生之间的讨论：可以是教师提问题，学生集体协作解决;可以是学生提问题，学生解决;也可以采用学生授课等形式。其中学生之间的讨论，主要以自由组合为主。笔者在课堂教学中也在一定程度上“退居二线”了，教师的主要任务是组织教学。笔者认为教学方法的选择应体现以人为主的教学理念，我们所面对的是活生生的人，每一位学生的情况又不同，因此，在选择教学方法时，不能局限于一两种方法，应该让学生发挥各自的特长，允许一道题目有多种解题的方法，然后通过讨论让学生明确哪一种方法较为简便，还要向学生提倡具有创新性的解题方法。这样的教学方法既可以让学生明白解决一个问题可以有多种多样的方法，又可以让学生学会选择合理的方法，提高解题能力。

在数学课堂上，培养学生的逆向思维也是思维灵活性的一种表现，因此应重视培养学生的逆向思维，引导学生进行逆向思维和逆向推理，做到既善于从左到右的正向运动，又能够从右到左的逆向运动。为此，必须把握时机，既要在概念、性质、法则的教学中强化逆向思维，又要在习题课、练习课中强化逆向思维。

三、培养学生思维的多向性

多向思维即从尽可能多的方面来考察同一问题，使人们的思维不拘泥于一个途径，一种方法，例如，笔者在教七年级（下）“多项式与多项式相乘”这一节里，有一道题目：“有一块菜地，长为a，宽为m;现在将它的长增加b，宽增加n，求扩大后菜地的面积。”如图所示：

问：你有几种表示扩大后菜地面积的方法？

学生思考、讨论、踊跃发言，最后有以下几种方法：（1）（a+b）（m+n）;（2）am+an+bm+bn;（3）（a+b）m+（a+b）n;（4）（m+n）a+（m+n）b.

所以有（a+b）·（m+n）=（a+b）m+（a+b）n=am+bm+an+bn

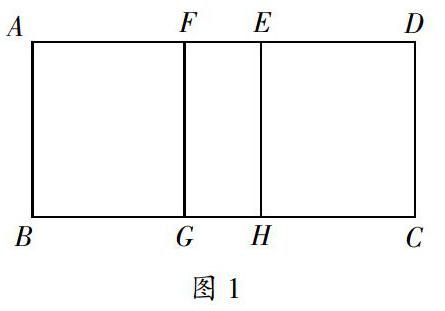
由于同学们的积极探讨、主动发言，多项式与多项式的乘法通过乘法分配律转化成单式与多项式的乘法，最后计算出结果。这是“一题多解，让学生自己动脑思考，最后发掘出多项式与多项式相乘的法则。也可以进行“一题多变”来训练学生的思维。改变条件或结论，使学生养成广泛联想和类比的思维习惯，鼓励学生从多角度、多层次、多方向解决问题。例如，在学习过“平移”知识后，笔者让孩子们看这样一例：例：图1中，在长为acm、宽为bcm的长方形ABCD中，剪去一个长为1cm的小长方形EFGH（它的位置不确定），则余下的部分面积是多少？

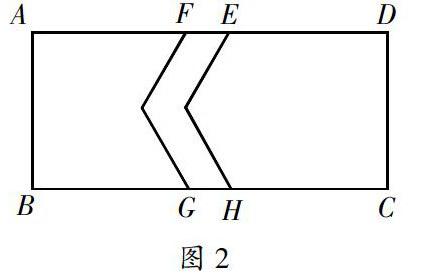
变化一：若问题变成如图2，小长方形被变成两个等宽的平行四边形，EF仍为1cm，则余下的部分面积是多少？

变化二：若问题变成如图3，小长方形被变成多个等宽的平行四边形，EF仍为1cm，则余下的部分面积是多少？

四、培养学生思维的创新性

人类智慧的核心是创造性思维，而创造性思维的核心就是发散思维。发散思维是客观存在的，它是指对于同一问题，从不同角度、不同层次、不同方面出发，得出多种多样的设想和解决问题途径的思维过程。培养学生的发散能力，有助于他们从不同角度分析问题，以达到问题的解决。

发散思维具有多向性、变异性、独特性的特点，即思考问题时注重多途径多方案，解决问题时举一反三，触类旁通，给学生提供丰富的思维材料，抓好思维飞跃点，精心设置问题情境，抓好情感激发点，常用方法有：

1. 题型发散法

题型发散法是将有发散点的典型问题变换题型，进行发散。例：

（1）如果n是方程x²+mx+n=0（n≠0）的根，则m+n=（）

A. -1/2B. -1 C. 1/2D. 1

（2）方程2/（1-x）²=1/（x+1）-1的解是（）

A. 2 B. 0 C. -1 D. 2、-1

2. 變形发散法

变形发散法是通过代数式、不等式、函数等形式的改变，达到化繁为简、化难为易的目的再或者适当的运用对称、平移、旋转、位移、等积等几何变换，将那些分散、远离的条件从图形的某一部分转移到适当的位置上得以相对集中，从而发现解题的思路，达到巧妙解题的目的的发散思维。如：

例1.已知一个多边形的每个内角都等于135°，求这个多边形的边数。

解：设这个多边形的边数为n，则（n-2）·180=135°·n，解之得n=8，∴这个多边数是8

变式1  已知一个多边形内角和是1080°，求这个多边形的边数。

变式2  已知一个多边形的边数是8，求这个多边形的内角和。 以上两变式的解法都用原例同一关系式，解法略。

变式3  已知一个正多边形的外角是45°，求这个正多边形内角和。

解：设这个多边形的边数为n，而它的每个外角都等于45°，则n·45°=360°∴n=8

变式4  已知多边形的内角和与某一个外角的度数总和为1180°，求此多边形的边数。

解：设这个多边形为n边形，且这个外角为x度，则0°

（n-2）·180°+x=1180°，即（n-2）180°=1180°-x

由于左边是180°的整数倍，故1180°-x也必是180°的整数倍。即1180°-x=n·180°（n为自然数），故x必是1180°÷180°的余数1180°÷180°=8……100°

∴x=100°，由（n-2）180°=1180°-100°，得n=8

以上变式从不同角度调换例题的题设和结论，解法不尽相同，但是它们都依据了多边形内角和公式和外角和公式，这样教学，为学生从不同角度去观察问题，思考问题，用不同方法解决问题提供了丰富的材料，使学生的知识在更广阔的领域内进行循环，观察的灵活性得以培养和训练，在突破学生定向性思维模式上具有一定的意义。把握它的实质，克服思维的静止孤立状态，培养学生发散机智，提高发散思维的流畅性。

总之，新课程教学中，教师是学生学习的合作者、引导者和参与者。教师的职责已由知识的传授转向促进学生发展，要引导学生学会观察、学会思考、学会如何学习、培养终身学习的能力，而在数学课中培养学生的数学思维能力则是教学的根本目的，这需要教师充分利用教材内容，通过数学知识的学习，努力培养和提高学生的数学思维能力。数学能力的培养不是一朝一夕的事，坚持正确的教学方向，贯彻先进的教学理念，既注重知识信息的传播，又不断努力开发学生的创造潜能，教会学生学习的方法，数学教育事业才会欣欣向荣。