论皮尔士的溯因逻辑*

李烜

西南大学政治与公共管理学院哲学系

lixuan5332218@163.com

1 引言

皮尔士在研究十九世纪逻辑的过程中提出了溯因推理，它是不同于演绎和归纳的第三种推理。最初皮尔士认为演绎是数学的逻辑，而归纳和溯因则是科学发现的逻辑。但是，后来皮尔士认为，三种推理不过代表了科学发现过程的三个不同阶段。任何实际推理过程都不是单一的，都要遵循“溯因——演绎——归纳”的模式。第一阶段是溯因，形成猜想或假设，以便解释令人惊讶的事实。第二阶段是演绎，从假设出发必然得出结论。第三阶段是归纳，检验结论，概括结论得到一般性结论。即便在数学证明中，实际推理过程也是复杂的，而不是单一的。对于溯因这种推理，皮尔士的解释经历从早期到晚期的三种不同形式。本文将这三种形式分别概括为三段论式、假言式和探究式。对这三种形式，本文分别从三段论、命题逻辑和动态学的角度进行逻辑分析，建立它们的分析模型。探究式溯因推理是皮尔士晚期对溯因做出的较为成熟的代表性的解释，从动态学的角度可以重建皮尔士的溯因逻辑，将溯因逻辑理解为科学猜想随着新数据的出现而不断变化的过程。

2 皮尔士溯因推理的三副面孔

在1860–1870年代的著作中，皮尔士运用三段论说明三种基本的推理形式：演绎、归纳和溯因，分别对应于下图中三种三段论的格：

图1.三段论的格

对于第二格，皮尔士举了这样的例子：光是可极化的。以太波是可极化的。所以，光是以太波。（W1：427，18661W为参考文献[14]，后接卷数与页码，下同。）皮尔士认为，这种假设论证是唯一一种能够使我们“看到事物的为什么”（W1：428）的论证形式。

在1870年代到1880年代，皮尔士将溯因和归纳描述为演绎三段论的逆推形式（[13]）。在图1中，第一格的大前提称为规则，小前提称为例子，结论称为结果。溯因就是从规则和结果到例子的推理。归纳就是从例子和结果到规则的推理。演绎就是从规则和例子到结果的推理。下面是皮尔士给出的例子：

图2.三种推理举例

皮尔士把演绎推理看做最可靠的推理，而溯因推理是最不可靠的。但是，正是由于溯因推理是制造假设的推理，它才能广泛用来处理不确定性和科学猜想。运用三段论的格，早期皮尔士对溯因推理做出了一种解释，我们称之为三段式溯因推理。

皮尔士的第二种对溯因的解释是对三段论式溯因推理的推广，也是常见的关于溯因推理的“经典”解释。这种解释可以表述如下：

图3.假言式溯因推理

这个模式是从观察到的令人惊讶的事实C出发，根据假言条件句“A蕴涵C”，推出A可能是C的解释或原因。这种对溯因推理的解释流传较广，几乎成为溯因推理的经典模式（[17]）。皮尔士在1903年第七次哈佛讲座中发表了这个模式（CP 5.1982CP为文献[15]，后接卷数和页码。），但是此后皮尔士几乎没有提到这种解释。可见假言式溯因推理并非皮尔士最满意的表述形式。

假言式溯因推理在后来的文献中有着多种不同的再解释，其中一种最重要的说法称为最佳推理解释（IBE），认为溯因推理仅仅是寻求最佳解释的推理过程。这里要澄清溯因与IBE的区别。溯因推理允许做出多个不同的假设，而IBE只允许一个最佳假设。溯因推理是建立科学理论的方法，而IBE是比较假设的解释性价值的方法。3辛迪卡也批评了把溯因推理解释为IBE的做法。他认为溯因推理的关键因素就是“猜想”（[7]）。文献[2]也比较了溯因推理与IBE的区别。

皮尔士的第三种对溯因的解释出现于1905年7月16日他写给威比（Victoria Welby）的信中。在溯因中，大前提是陈述句，而结论是疑问句。皮尔士对这种疑问语气进行了解释：

这种“疑问语气”意思不是观念的单纯无意义的娱乐。它的意思是，依赖于从知道任何/有的S是M产生的优势，某些耗费就是明智的，只要这些耗费在假设它真的条件下行动起来是安全的。这就是那种所谓的从后果到前提的推理。它与否定后件推理（Modus Tollens）有关，因此

与“疑问的”相比，结论的语气可以更精确地成为“探究的”，可以表达如下：“探究A是否是真的。”

这种推理可以称为“从惊奇到探究的推理”。（[5]，1905年7月16日）

这种推理称为探究式溯因推理。“探究”这个概念是非常有意义的，在科学发现中有八个方面与它有关：(1)注意到惊奇的现象；(2)寻找相关条件；(3)提出问题；(4)做出猜想；(5)说明该猜想至少表面上看能够解释惊奇的现象；(6)采纳该猜想，它是可想象的、可理解的、合理的；(7)对假设的检验进行成本收益分析；(8)在特定条件下根据这些假设采取行动。这些都属于探究过程的溯因推理阶段。这个阶段的核心是形成科学猜想。在1905年之后，皮尔士将溯因描述为从惊奇到探究的推理过程，这也是比较成熟的关于溯因推理的解释，应该是溯因推理的最佳解释。

皮尔士从早期到晚期提出了三种形式的溯因推理。关于溯因推理的一般性研究参见[11,12,16,18]。虽然皮尔士有许多解释，但是对它们从逻辑的角度进行分析，形成关于溯因推理的逻辑理论，确是还没有完全实现的任务。在接下来的三节中，要分别对这三种形式的溯因推理从逻辑上加以解释。尤其是探究式溯因推理，我们将赋予它一种动态解释，建立一种动态逻辑，由此使溯因逻辑究竟是什么的问题得到部分回答。

3 三段论式溯因推理

皮尔士早期的三段论式溯因推理是把图1中三段论第二格作为溯因推理的形式。亚里士多德的三段论只有三个格（图1）4亚里士多德的三段论系统只有三个格。后来传统逻辑加上第四格。第四格是否是亚里士多德提出的，这一点有争议。，每个格有64个式，总共192个式。这些式是在格上增加全称量词“所有”、存在量词“有的”、系词“是”和否定“不是”得到的。基本命题形式是“S是P”，增加量词和系词及否定之后有四种形式：全称肯定命题“所有S是P”（称为A命题），全称否定命题“所有S不是P”（称为E命题）；特称肯定命题“有的S是P”（称为I命题），特称否定命题“有的S不是P”（称为O命题）。图1中三段论第二格，如果补充否定，那么也有64个式。但是这个格的前提和结论都是肯定命题，因此只有A和I两种命题，于是只有如下8个三段论式：AAA、AAI、AIA、AII、IAA、IAI、IIA、III。这8个式都不是有效的，如下文恩图足以反驳所有这些式：

图4.三段式溯因推理的非有效性

这说明三段式溯因推理都不是逻辑上有效的推理，其结论都不是必然从前提得到的。图1中第一格是演绎推理。在所有8个三段式中，第一格只有AAA、AAI和IAI等3个逻辑有效式。类似地，图1中第三格（归纳推理）只有AAI、AII、IAI等3个逻辑有效式。这也反映了皮尔士的说法，溯因推理是最不可靠的。

那么皮尔士以三段论的格来区分演绎推理、溯因推理和归纳推理究竟是什么意思？演绎推理是必然性推理，结论必然从前提得出。溯因推理和归纳推理都不是必然性的。从图2的例子来看，可以推测皮尔士的意思是考虑AAA式。演绎推理第一格的AAA是有效的，第二格和第三格的AAA式都不是有效的。具体来说，溯因推理的AAA式与归纳推理的AAA式非有效的方式可以不同。图4说明了三段论式溯因推理AAA式的非有效性。下图5则说明了三段论式归纳推理AAA式的非有效性：

图5.三段论式归纳推理的非有效性

第二格AAA式的反驳模型如下：大前提（规则）“所有P是M”是真的，即P包含于M；小前提（结果）“所有S是M”是真的，即S包含于M；而结论“所有S是P”是假的。第三格AAA式的反驳模型如下：大前提（规则）“所有M是P”是真的，即M包含于P；小前提（结果）“所有M是S”是真的，即M包含于S；而结论“所有S是P”是假的。

在科学探究中，溯因推理的用处是显而易见的，从结果中事物的情况和规则猜测事物的原因。当然这里要假设规则和结果都是真的，溯因推理才有意义。但是三段论式处理溯因推理的能力有限。考虑下面这个推理：

规则： 如果火星曾经有液态水，那么火星地表一定有水流的痕迹。

结果： 火星地表有水流的痕迹。

例子： 火星曾经有液态水。

假设规则和结果都是真的。结论具有合理性，它解释了观测得到的结果。这个推理应该算作溯因推理，它既不是演绎推理，也不是归纳推理。但是它无法以三段论形式来表述。命题联结词在三段论中无法定义，量词在命题逻辑中也无法定义。

4 假言式溯因推理

皮尔士推广三段论式溯因推理而得到假言式溯因推理，这种形式可以用来处理前面指出的无法用三段论处理的例子。图3给出了假言式溯因推理的一般形式。从逻辑上看，它是一种命题逻辑推理。在命题逻辑中，我们用“A→C”表示“如果A，那么C”，称为假言命题。那么假言式溯因推理的格式可以写成命题逻辑中的肯定后件式推理：

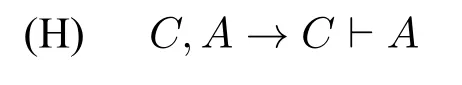
肯定后件式在命题逻辑中不是有效的。这也是溯因推理的特点：结论不是必然从前提得出的，图3中结论的限定语“有理由认为”就是这个意思。那么从逻辑上如何来分析“有理由认为”这个限定语？让我们来看(H)为什么不是有效的。

首先，在命题逻辑中我们假定任何命题都是真的或假的，而且非真即假、非假即真。在(H)中有两个命题A和C，它们的真假组合只有四种情况：TT、TF、FT、FF。在推理之前可能的情况只有这四个。其次，“A→C”这个假言命题只有在A真而C假（即TF）这种情况下才是假的，在其它情况下都是真的。由这两点可知，在FT这种情况下（A假而C真），(H)的结论是假的，而前提都是真的。所以(H)不是有效的。

如果我们从信息动态变化的角度来看，(H)还可以告诉我们溯因推理更多的东西。首先假定有A和C两个命题，初始的信息状态有四个TT、TF、FT、FF，它们构成信息状态的范围。现在对于(H)这个推理，依次输入两个前提。输入前提C相当于肯定C是真的（C是一个令人惊讶的事实），于是信息状态的范围改变为：TT、FT。

这个变化是删除了使C假的两个状态。下面继续输入前提A→C，即肯定A→C是真的。此时没有任何状态会被删除，在TT和TF两个状态上，A→C都是真的。于是我们得到最终的信息状态范围，在这个范围中，A可以是真的，也可以是假的。因此，有理由认为A是真的，A真是可能的。

演绎推理也可以进行这样的动态分析。考虑否定后件推理(MT)¬C,A→C⊢¬A，其中¬表示否定。从四个初始信息状态出发，经过两次输入而达到结论。第一次是输入¬C而产生的信息变化，删除了C为真的两个状态。第二次是输入A→C而产生的信息变化，删除了A→C为假的状态TF。最后只剩下状态FF，其中A是假的，所以¬A是真的。演绎推理过程可以这样来表述，一个从前提A1,...,An到结论B的演绎推理是这样一个信息变化过程，在初始2n+1个信息状态中，依次输入信息A1,...,An，在最终达到的信息状态范围中所有状态上B都是真的。一种特殊情况是所有信息都被删除，例如考虑推理¬A,A⊢B，那么显然B在最终“所有”状态上都是真的，因为最后的范围中没有状态存在。

相反，就溯因推理而言，在最后得到的信息状态范围中，结论在一些状态上真，而在另一些状态上假。这也充分说明了溯因推理的或然性。虽然假言式溯因推理有一定的道理和实用价值，在科学探究中这种推理形式常常被使用，但是它却忽略了结论“A”作为面对令人惊讶的事实“C”时的“猜想”意义。溯因推理本质上就是形成科学猜想的过程，而且面对同一个事实C，可以形成多个不同的猜想。不同的猜想也会受到新的证据的支持或反驳，这样一些猜想会被排除，而一些猜想在新的数据出现时仍然能够支持结论。如何研究形成猜想的动态变化过程，恰恰是研究溯因推理应该回答的问题。

5 探究式溯因推理

皮尔士晚期提出的探究式溯因推理正是突出科学发现中的“猜想”的努力。前面提到，皮尔士在1905年认为溯因推理是从后果到前提的推理，为了突出溯因推理中的猜想特征，皮尔士用疑问句作为溯因推理的结论。根据皮尔士的例子，探究式溯因推理的形式可以写成：

结论“?A”表示“探究A是否是真的”。这与前面提到的假言式溯因推理有较大的差异，结论从陈述语气改为疑问语气。疑问句“?A”并不像问句逻辑中那样，表示将A真和A假的情况划分为两个等价类，而是表示对A是否真的探究5在近年来的问句逻辑中，处理疑问的动态方法将提出问题看作对所有信息状态的等价类划分，对于要求“是/不是”回答的问题，被划分的等价类只有两个（[1]）。。探究过程就是溯因推理过程。我们首先来看杜威在《我们如何思维》中所举的一个例子：

从我每天过河的渡轮上方夹板水平看去，是一个白色的长杆子，末端有一个镀金球。我第一次看见它就联想到旗杆；它的颜色、形状和镀金球与这个想法是一致的，这些理由似乎足以让我觉得这个信念是合理的。但很快困难出现了。杆子接近水平线，这个位置对于旗杆来说很不寻常；在另一个位置上，没有滑轮、环或者挂旗子的绳子；最后，其它位置还有两个垂直的东西，有时旗子是从哪里飘起来的。似乎有可能那个杆子在那儿不是挂旗子的。

然后我尝试想想这个杆子所有可能的目的，考虑最适合它的目的：(a)可能它是装饰。但是所有渡轮、甚至是拖轮都有类似的杆子，因而这个假设被否认了。(b)可能他是无线电终端。但是同样的考虑使得这不可能。此外，这样一个终端更自然的位置是船的最高处，在驾驶室顶端。(c)它的目的可能是指示船前进的方向。

为了支持这个结论，我发现这根杆子比驾驶室低一些，驾驶员可以很容易看见它。此外，末端比基础端足够高，从驾驶室的位置看，它似乎超出船前面投射很远。此外，驾驶员靠近船前部，需要航向指引。拖船也需要一根杆子达到这样的目的。这个假设要比其它假设更有可能性，所以我接受了它。我形成了结论，这个杆子是用来向驾驶员指示船前进的方向，使他正确地驾驶。（[3]）

杜威的这个例子虽然是关于日常生活中的推理，但是它也与科学探究一样使用溯因推理6例如开普勒发现天体的椭圆形轨道的案例（[8]）。。最初令人惊讶的事实是下面这个命题：

(F)有一根白色杆子，在顶端装有镀金球，而且靠近渡船的上部夹板。然后下面四个疑问句被认为是可能的：

(A1)这根白色的长杆子是旗杆吗？

(A2)它是装饰吗？

(A3)它是无线电终端吗？

(A4)它是指引船前进方向的杆子吗？这四个假设在某个阶段都支持事实F。恰恰是这个事实F令人联想到四个可能的原因。这样我们有四个可能的猜想：

(C1)在其它位置有类似的旗杆。

(C2)每艘船在相应位置都有类似的杆子。

(C3)类似的船有类似的杆子，无线电终端应该在更高的位置。

(C4)杆子低于驾驶室。

当(C1)这个事实被联想到，猜想(A1)不再支持(C1)，它被反驳。同样，当(C2)和(C3)依次出现之后，猜想(A2)和(A3)分别被反驳。最后只剩下猜想(A4)，它支持事实(C4)。这个猜想的动态变化过程就是溯因推理过程，或者称之为探究过程。现在来看如何对探究式溯因推理进行逻辑分析。

猜想是一种命题态度。这里“命题态度”意思是将猜想看做是关于命题的一种态度。其它命题态度还有“知道”、“相信”等等。它究竟是一种怎样的命题态度？它与信念、知识等命题态度又有何差别？这里仅以辛迪卡的知识和信念逻辑为例来简单讨论这个问题（[6]）。

第一、如果命题A是猜想，那么它是信念。也就是说，猜想是一种拟信念。这一点符合我们关于猜想和信念的直觉，如果一个人猜想A可以支持某事实C，那么A必定被相信是C的解释或原因。那么是否信念都是猜想呢？我认为不是。一个证据是考虑信念的正内省性质：如果一个人相信A，那么他相信他自己相信A。但是对于猜想来说，一个人关于自己的猜想的猜想是没有什么意义的。对于负内省性质来说也是如此：如果一个人不相信A，那么他相信自己不相信A。但是对于猜想而言，假设一个人没有猜想A，这并不意味着他猜想自己没有猜想A。猜想和信念的一点差别是，内省性质对信念可以成立，对猜想则是没有意义的。

第二、还有一些原理对于猜想来说是可以成立。例如，猜想必定是一致的。这就是说，不能同时猜想A和猜想非A。猜想是单调性的，即如果A蕴涵B，那么猜想A必定蕴涵猜想B。猜想还是封闭的，即如果猜想“A”并且猜想“B”，那么一定会猜想“A并且B”。但是猜想不具备正规性，一个命题A是重言式并不必然导致猜想A。这些都是猜想的基本逻辑性质，如果希望从公理系统的角度给出一个关于猜想的逻辑系统，这是可以做到的。

现在我们转向猜想的动态变化。一般地说，动态是在动态认知逻辑中引入的一种关于信息变化的机制，在语言方面引入动态算子，在模型上引入模型更新的运算（[4]）。为了显示猜想的动态变化机制，例如杜威的例子中猜想的动态变化，先引进一些基本概念。以W表示所有状态的集合，任何命题都解释为W的一个子集。集合W上的一个邻域函数N是从W到W的幂集之幂集的函数，也就是说，对每个状态w，N(w)是W的幂集的一个子集，称为w的邻域，其中每个集合分别代表一个“潜在的命题”，也就是在状态w上所有猜想的集合。在N(w)中有四个猜想是杜威例子中给出的。

我们用“!C”表示事实C被联想或观察到。当C1出现时，N(w)变化为NC1(w)，其中A1被删除了，因为A1这个猜想不支持C1这个事实。进一步而言，经过C2和C3出现，最终得到w的领域为NC1C2C3(w)，其中只剩下一个猜想A4。当然，A4也可能被新的事实删除，这样就要求寻找新的猜想。在杜威的例子中，A4是被确定下来作为最初令人惊讶的事实F的合理猜想。这个猜想与经验事实一致。这就是猜想的动态变化过程。这个过程完全可以形式化，从而得到一个关于猜想动态变化的逻辑理论，它就是探究式溯因推理的逻辑（[9]）。

这种动态变化的逻辑理论与内波穆塞诺·费尔南德斯等人关于溯因推理提出的动态认知逻辑处理方法（[10]）是不同的。最主要的不同在于，本文提出的处理方法是在邻域模型上来解释猜想的动态变化，而后者是在克里普克模型中通过引入合理性次序来分析溯因过程。此外，本文是在分析皮尔士的疑问解释的基础上进行的分析，它与最佳解释模型是不同的。在IBE解释中，假设在众多猜想中有一个最好的猜想。但是前面的动态分析不假定这一点。皮尔士的溯因推理与最佳解释推理是有区别的。

6 结语

本文对皮尔士三个阶段对溯因推理的三种解释分别进行了逻辑分析，从形式上解释了三种溯因推理形式。三段论式溯因推理和假言式溯因推理都过于简单，没有充分体现溯因推理中的猜想因素以及猜想的动态变化过程，只有探究式溯因推理才是比较成熟的溯因推理形式。最终可以达到了一种溯因推理逻辑，这里所说的逻辑，不是说溯因推理的有效性，溯因推理不是有效的演绎推理，而是将猜想处理为命题态度，进而从模态逻辑的角度提出的一种逻辑，并且可以处理猜想的动态变化。当然，关于猜想还有许多问题值得进一步研究。比如集体猜想和个体猜想的差异、集体猜想及其动态变化的逻辑等等。此外，前面我们讨论过把猜想看做一种“前信念”，猜想的性质在信念逻辑中是成立的，但反之不必然。如何刻画猜想的性质，这也是一个可以从哲学和逻辑上加以分析的问题。