Neighborhood Contingency Logic:A New Perspective*
Jie Fan
School of Humanities,University of Chinese Academy of Sciences
jiefan@ucas.ac.cn
Abstract.In this paper,we propose a new neighborhood semantics for contingency logic,by introducing a simple property in standard neighborhood models.This simplifies the neighborhood semantics given in Fan and van Ditmarsch(2015),but does not change the set of valid formulas.Under this perspective,among various notions of bisimulation and respective Hennessy-Milner Theorems,we show that c-bisimulation is equivalent to nbh-∆-bisimulation in the literature,which guides us to understand the essence of the latter notion.This perspective also provides various frame definability and axiomatization results.
1 Introduction
Under Kripke semantics,contingency logic(CL for short)is non-normal,less expressive than standard modal logic(ML for short),and the five basic frame properties(seriality,reflexivity,transitivity,symmetry,Eucludicity)cannot be defined in CL.This makes the axiomatizations of CL nontrivial:although there have been a mountain of work on the axiomatization problem since the 1960s[15,9,10,11,12],overK,D,T,4,5 and any combinations thereof,no method in the cited work can uniformly handle all the five basic frame properties.This job has not been addressed until in[5],which also contains an axiomatization of CL onBand its multi-modal version.This indicates that Kripke semantics may not be suitable for CL.
Partly inspired by the above motivation(in particular,the non-normality of CL),and partly by a weaker logical omniscience in Kripke semantics(namely,all theorems are known to be true or known to be false),a neighborhood semantics for CL is proposed in[4],which interprets the non-contingency operator∆in a way such that its philosophical intuition,viz.necessarily true or necessarily false,holds.However,under this(old)semantics,as shown in[4],CL is still less expressive than ML on various classes of neighborhood models,and many usual neighborhood frame properties are undefinable in CL.Moreover,based on this semantics,[1]proposes a bisimulation(called ‘nbh-∆-bisimulation’there)to characterize CL within ML and within first-order logic(FOL for short),but the essence of the bisimulation seems not quite clear.
In retrospect, no matter whether the semantics for CL is Kripke-style or neigborhoodstyle in the sense of[4],there is an asymmetry between the syntax and models of CL:on the one hand,the language is too weak,since it is less expressive than ML over various model classes;on the other hand,the models are too strong,since its models are the same as those of ML.This makes it hard to handle CL.1Analogous problem occurs in the setting of knowing-value logic[13,14].
Inspired by[6],we simplify the neighborhood semantics for CL in[4],and meanwhile keep the logic(valid formulas)the same by restricting models.This can weaken the too strong models so as to balance the syntax and models for CL.Under this new perspective,we can gain a lot of things,for example,bisimulation notions and their corresponding Hennessy-Milner Theorems,and frame definability.Moreover,we show that one of the bisimulation notions is equivalent to the notion of nbh-∆-bisimulation,which helps us understand the essence of nbh-∆-bisimulation.We also obtain some simple axiomatizations.
2 Preliminaries
2.1 Language and old neighborhood semantics
First,we introduce the language and the old neighborhood semantics of CL.Fix a countable set Prop of propositional variables.The language of CL,denotedL∆,is an extension of propositional logic with a sole primitive modality∆,wherep∈Prop.

∆φis read “it is non-contingent thatφ”.∇φ,read “it is contingent thatφ”,abbreviates¬∆φ.
A neighborhood model forL∆is defined as that for the languageL□of ML.That is,to sayM=⟨S,N,V⟩is a neighborhood model,ifSis a nonempty set of states,N:S→22Sis a valuation assigning each propositional variable inSa set of neighborhoods,andV:Prop→2Sis a valuation assigning each propositional variable in Prop a set of states in which it holds.A neighborhood frame is a neighborhood model without any valuation.
There are a variety of neighborhood properties.The following list is taken from[4,Def.3].
Definition 1(Neighborhood properties)
(n):N(s)contains the unit,ifS∈N(s).
(r):N(s)contains its core,if∩N(s)∈N(s).
(i):N(s)is closed under intersections,ifX,Y∈N(s)impliesX∩Y∈N(s).
(s):N(s)issupplemented,orclosed under supersets,ifX∈N(s)andX⊆Y⊆SimpliesY∈N(s).We also call this property ‘monotonicity’.
(c):N(s)isclosed under complements,ifX∈N(s)impliesSX∈N(s).
(d):X∈N(s)impliesSX/∈N(s).
(t):X∈N(s)impliess∈X.
(b):s∈Ximplies{u∈S|SX/∈N(u)}∈N(s).
(4):X∈N(s)implies{u∈S|X∈N(u)}∈N(s).
(5):X/∈N(s)implies{u∈S|X/∈N(u)}∈N(s).
FrameF=⟨S,N⟩(and the corresponding model)possesses such a propertyP,ifN(s)has the propertyPfor eachs∈S,and we call the frame(resp.the model)P-frame(resp.P-model).
Given a neighborhood modelM=⟨S,N,V⟩ands∈S,the old neighborhood semantics ofL∆[4]is defined as follows,whereφM⊩={t∈S|M,t⊩φ}.
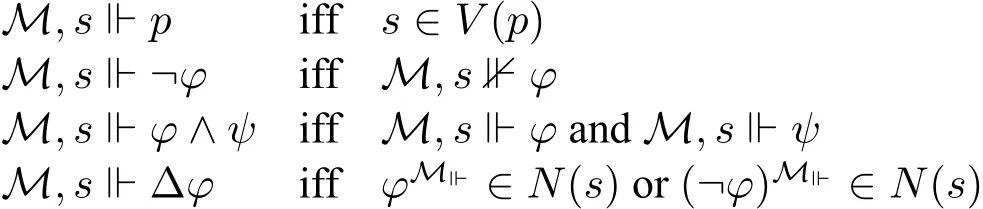
2.2 Existing results on old neighborhood semantics
Under the above old neighborhood semantics,it is shown in[4,Props.2-7]that on the class of(t)-models or the class of(c)-models,L∆is equally expressive asL□;however,on other class of models in Def.1,L∆is less expressive thanL□;moreover,noneof frame properties in the above list are definable in CL.
Based on the above semantics for CL,a notion of bisimulation is proposed in[1],which is inspired by the definition ofprecocongruencesin[8]and the old neighbourhood semantics of∆.
Definition 2(nbh-∆-bisimulation)LetM=⟨S,N,V⟩andM′=⟨S′,N′,V′⟩be neighborhood models.A nonempty relationZ⊆S×S′isanbh-∆-bisimulationbetweenMandM′,if for all(s,s′)∈Z,
(Atoms)s∈V(p)iffs′∈V′(p)for allp∈Prop;
(Coherence)if the pair(U,U′)isZ-coherent,2Let R be a binary relation.We say(U,U′)is R-coherent,if for any(x,y)∈ R,we have x ∈ U iff y ∈ U′.We say U is R-closed,if(U,U)is R-coherent.It is obvious that(∅,∅)is R-coherent for any R.then
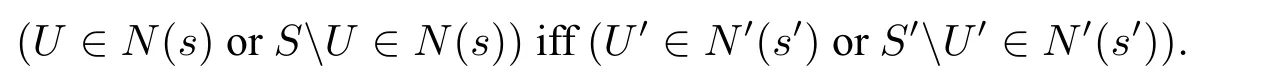
(M,s)and(M′,s′)isnbh-∆-bisimilar,notation(M,s)∼∆(M′,s′),if there is a nbh-∆-bisimulation betweenMandM′containing(s,s′).3In fact,the notion of nbh-∆-bisimilarity is defined in a more complex way in[1].It is easy to show that our definition is equivalent to,but simpler than,that one.
Although it is inspired by both the definition ofprecocongruencesin[8]and the old neighbourhood semantics of∆,the essence of nbh-∆-bisimulation seems not so clear.
It is then proved that Hennessy-Milner Theorem holds for nbh-∆-bisimulation.For this,a notion of∆-saturated model is required.
Definition 3(∆-saturated model) [1,Def.11]LetM=⟨S,N,V⟩be a neighborhood model.A setX⊆Sis∆-compact,if every set ofL∆-formulas that is finitely satisfiable inXis itself also satisfiable inX.Mis said to be∆-saturated,if for alls∈Sand all≡L∆-closed neighborhoodsX∈N(s),bothXandSXare∆-compact.
Theorem 1(Hennessy-Milner Theorem for nbh-∆-bisimulation) [1,Thm.1]On∆-saturated modelsMandM′and statessinMands′inM′,if(M,s)≡L∆(M′,s′),then(M,s)∼∆(M′,s′).
3 A new semantics for CL
As mentioned above,there is an asymmetry between the syntax and neighborhood models of CL,which makes it hard to tackle CL.In this section,we propose a new neighborhood semantics for this logic.This semantics is simpler than the old one,but the two semantics are equivalent in that their logics(valid formulas)are the same.
The new neighborhood semantics⊪and the old one⊩differ only in the case of non-contingency operator.

whereφM={t∈M|M,t⊪φ}.To say two models with the same domain arepointwise equivalent,if every world in both models satisfies the same formulas.
We hope that although we change the semantics,the validities are still kept the same as the old one.So how to make it out?Recall that non-contingency means necessarily true or necessarily false,which implies that∆p↔∆¬pshould be valid.However,although the formula is indeed valid under the old neighborhood semantics,it is invalid under the new one.In order to make this come about,we need make some restriction to the models.Look at a proposition first.
Proposition 1Under the new semantics,∆p↔∆¬pdefines the property(c).
ProofLetF=⟨S,N⟩be a neighborhood frame.
First,supposeFpossesses(c),weneedtoshowF⊪∆p↔∆¬p.Forthis,assume any modelMbased onFands∈Ssuch thatM,s⊪∆p,thuspM∈N(s).By(c),SpM∈N(s),i.e.,(¬p)M∈N(s),which means exactlyM,s⊪∆¬p.Now assumeM,s⊪ ∆¬p,we have(¬p)M∈N(s),that isSpM∈N(s).By(c),S(SpM)∈N(s),i.e.pM∈N(s),and thusM,s⊪ ∆p.HenceM,s⊪ ∆p↔∆¬p,and thereforeF⊪∆p↔∆¬p.
Conversely,supposeFdoes not possess(c),we need to showF̸⊪ ∆p↔∆¬p.By supposition,there existsXsuch thatX∈N(s)butSX/∈N(s).Definea valuationVonFasV(p)=X.We have nowpM=V(p)∈N(s),thusM,s⊪ ∆p.On the other side,V(¬p)=SX/∈N(s),thusM,s¬p.HenceM,sp→∆¬p,and thereforeF̸⊪ ∆p↔∆¬p. □
This means that in order to guarantee the validity∆p↔∆¬punder new semantics,we(only)need to ‘force’the model to have the property(c).Thus from now on,we assume(c)to be theminimalcondition of a neighborhood model,and call this type of model‘c-models’.
Definition 4(c-structures) A model is ac-model,if it has the property(c);intuitively,if a proposition is non-contingent at a state in the domain,so is its negation.A frame is ac-frame,if the models based on it arec-models.
The following proposition states that onc-models,the new neighborhood semantics and the old one coincide with each other in terms ofL∆satisfiability.
Proposition 2LetM=⟨S,N,V⟩be ac-model.Then for allφ∈L∆,for alls∈S,we haveM,s⊪φ⇐⇒M,s⊩φ,i.e.,φM=φM⊩.
ProofBy induction onφ∈L∆.The only nontrivial case is∆φ.
First,supposeM,s⊪ ∆φ,thenφM∈N(s).By induction hypothesis,φM⊩∈N(s).Of course,φM⊩∈N(s)or(¬φ)M⊩∈N(s).This entails thatM,s⊩∆φ.
Conversely,assumeM,s⊩ ∆φ,thenφM⊩∈N(s)or(¬φ)M⊩∈N(s).SinceMis ac-model,we can obtainφM⊩∈N(s).By induction hypothesis,φM∈N(s).Therefore,M,s⊪∆φ. □
Definition 5(c-variation)LetM=⟨S,N,V⟩be a neighborhood model.We sayc(M)is ac-variationofM,ifc(M)=⟨S,cN,V⟩,where for alls∈S,cN(s)={X⊆S:X∈N(s)orSX∈N(s)}.
The definition ofcNis very natural,in that just as“X∈N(s)orSX∈N(s)”corresponds to the old semantics of∆,X∈cN(s)corresponds to the new semantics of∆.It is easy to see that every neighborhood model has a solec-variation,that every suchc-variation is a c-model,and moreover,for any neighborhood modelM,ifMis already ac-model,thenc(M)=M.
Proposition 3LetMbe a neighborhood model.Then for allφ∈L∆,for alls∈M,we haveM,s⊩φ⇐⇒c(M),s⊪φ,i.e.,φM⊩=φc(M).
ProofThe proof is by induction onφ,where the only nontrivial case is∆φ.We have
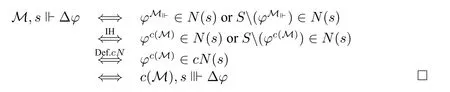
Let Γ ⊪cφdenote that Γ entailsφover the class of allc-models,i.e.,for eachc-modelMand eachs∈M,ifM,s⊪ψfor everyψ∈Γ,thenM,s⊪φ.With Props.2 and 3 in hand,we obtain immediately that
Corollary 1For all Γ∪{φ}⊆L∆,Γ⊪cφ⇐⇒Γ⊩φ.Therefore,for allφ∈L∆,⊪cφ⇐⇒⊩φ.
In this way,we strengthened the expressive power of CL,since it is now equally expressive as ML,and kept the logic(valid formulas)the same as the old neighborhood semantics.The noncontingency operator∆ can now be seen as a package of□ and∆in the old neighborhood semantics;under the new neighborhood semantics,on the one hand,it is interpreted just as□;on the other hand,it retains the validity∆p↔∆¬p.
4 c-Bisimulation
Recall that the essence of the notion of nbh-∆-bisimulation proposed in[1]is not so clear.In this section,we introduce a notion ofc-bisimulation,and show that this notion is equivalent to nbh-∆-bisimulation.Thec-bisimulation is inspired by both Prop.1 and the definition ofprecocongruencesin[8,Prop.3.16].Intuitively,the notion is obtained by just adding the property(c)into the notion of precocongruences.
Definition 6(c-bisimulation)LetM=⟨S,N,V⟩andM′=⟨S′,N′,V′⟩becmodels.A nonempty relationZ⊆S×S′is ac-bisimulationbetweenMandM′,if for all(s,s′)∈Z,
(i)s∈V(p)iffs′∈V′(p)for allp∈Prop;
(ii)if the pair(U,U′)isZ-coherent,thenU∈N(s)iffU′∈N′(s′).
We say(M,s)and(M′,s′)arec-bisimilar,written(M,s)↔c(M′,s′),if there is a c-bisimulationZbetweenMandM′such that(s,s′)∈Z.
Notethatbothc-bisimulation andc-bisimilarity are defined betweenc-models,rather than between any neighborhood models.L∆formulas are invariant underc-bisimilarity.
Proposition 4LetMandM′bec-models,s∈Mand
ProofLetM=⟨S,N,V⟩andM′=⟨S′,N′,V′⟩be bothc-models.By induction onφ∈L∆.The nontrivial case is∆φ.
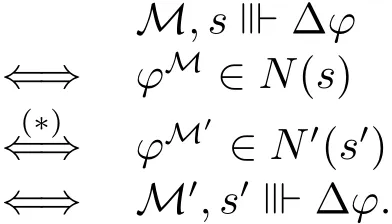
(∗)follows from the fact that-coherent plus the condition(ii)ofcbisimulation.To see why-coherent,the proof goes as follows:if for anythen by induction hypothesis,M,x⊪φiff
Now we are ready to show the Hennessy-Milner Theorem forc-bisimulation.Sincec-bisimulation is defined betweenc-models,we need also to add the propertycinto the notion of∆-saturated models in Def.3.
Definition 7(∆-saturatedc-model) LetM=⟨S,N,V⟩be ac-model.A setX⊆Sis∆-compact,if every set ofL∆-formulas that is finitely satisfiable inXis itself also satisfiable inX.Mis said to be∆-saturated,if for alls∈Sand all≡L∆-closed neighborhoodX∈N(s),Xis∆-compact.4Note that we do not distinguish≡L∆ here from that in Def.3 despite different neighborhood semantics.This is because as we show in Prop.2,on c-models the two neighborhood semantics are the same in terms of L∆satisfiability.Thus it does not matter which semantics is involved in the current context.
In the above definition of∆-saturatedc-model,we write“Xis∆-compact”,rather than “bothXandSXare∆-compact”,since under the condition thatX∈N(s)and the property(c),these two statements are equivalent.Thus each∆-saturatedc-model must be a∆-saturated model.
We will demonstrate that on∆-saturatedc-models,L∆-equivalence impliesc-bisimilarity,for which we prove that the notion of c-bisimulation is equivalent to that of nbh-∆-bisimulation,in the sense that every nbh-∆-bisimulation(between neighborhood models)is a c-bisimulation(betweenc-models),and vice versa.By doing so,we can see clearly the essence of nbh-∆-bisimulation,i.e.precocongruences with property(c).
Proposition 5LetM=⟨S,N,V⟩andM′=⟨S′,N′,V′⟩be neighborhood models.IfZis a nbh-∆-bisimulation betweenMandM′,thenZis a c-bisimulation betweenc(M)andc(M′).
ProofSuppose thatZis a nbh-∆-bisimulation betweenMandM′,to showZis a c-bisimulation betweenc(M)andc(M′).
First,one can easily verify thatc(M)andc(M′)are bothc-models.
Second,assume that(s,s′)∈Z.SinceMandc(M)have the same domain and valuation,item(i)can be obtained from the supposition and(Atoms).For item(ii),let(U,U′)beZ-coherent.We need to show thatU∈cN(s)iffU′∈cN′(s′).For this,we have the following line of argumentation:U∈cN(s)iff(by definition ofcN)(U∈N(s)orSU∈N(s))iff(by(Coherence))(U′∈N′(s′)orS′U′∈N′(s′))iff(by definition ofcN′)U′∈cN′(s′). □
Proposition 6LetM=⟨S,N,V⟩andM′=⟨S′,N′,V′⟩bec-models.IfZis a c-bisimulation betweenMandM′,thenZis a nbh-∆-bisimulation betweenMandM′.
ProofSuppose thatZis a c-bisimulation betweenc-modelsMandM′,to showZis a nbh-∆-bisimulation betweenMandM′.Assume that(s,s′)∈Z,we only need to show(Atoms)and(Coherence)holds.(Atoms)is clear from(i).
For(Coherence),letthepair(U,U′)isZ-coherent.Thenby(ii),U∈N(s)iffU′∈N′(s′).We also have that(SU,S′U′)isZ-coherent.Using(ii)again,we infer thatSU∈N(s)iffS′U′∈N′(s′).Therefore,(U∈N(s)orSU∈N(s))iff(U′∈N′(s′)orS′U′∈N′(s′)),as desired. □
Since everyc-variation of ac-model is just the model itself,by Props.5 and 6,we obtain immediately that
Corollary 2LetM=(S,N,V)andM′=⟨S′,N′,V′⟩be bothc-models.ThenZis ac-bisimulation betweenMandM′iffZis an nbh-∆-bisimulation betweenMandM′.
Theorem 2(Hennessy-Milner Theorem forc-bisimulation) LetMandM′be∆-saturatedc-models,ands∈M,s′∈M′.If for all
ProofSupposeMandM′are∆-saturatedc-modelssuchthatforallφ∈L∆,M,s⊪By Prop.2,we have that for allM′,s′⊩φ.Since each∆-saturatedc-model is a∆-saturated model,by Hennessy-Milner Theorem of nbh-∆-bisimulation(Thm.1),we obtain(M,s)∼∆(M′,s′).Then by Coro.2,we conclude that
5 Monotonic c-bisimulation
This section proposes a notion of bisimulation for CL over monotonic,c-models.This notion can be obtained via two ways:one is to add the property of monotonicity(s)intoc-bisimulation,the other is to add the property(c)into monotonic bisimulation(for ML).5For the notion of monotonic bisimulation,refer to[7,Def.4.10].For the sake of reference,we call the notion obtained by the first way‘monotonicc-bisimulation’,and that obtained by the second way ‘c-monotonic bisimulation’.We will show that the two notions are indeed the same.
Definition 8(Monotonicc-bisimulation)LetM=⟨S,N,V⟩andM′=⟨S′,N′,V′⟩bebothmonotonic,c-models.A nonempty binary relationZisamonotonicc-bisimulationbetweenMandM′,ifsZs′implies the following:
(i)sands′satisfy the same propositional variables;
(ii)If(U,U′)isZ-coherent,thenU∈N(s)iffU′∈N′(s′).
(M,s)and(M′,s′)is said to bemonotonic c-bisimilar,written(M,s)↔sc(M′,s′),if there is a monotonicc-bisimulation betweenMandM′such thatsZs′.
Definition 9(c-monotonic bisimulation)LetM=⟨S,N,V⟩andM′=⟨S′,N′,V′⟩be both monotonic,c-models.A nonempty binary relationZis ac-monotonic bisimulationbetweenMandM′,ifsZs′implies the following:
(Prop)sands′satisfy the same propositional variables;
(c-m-Zig)ifX∈N(s),then there existsX′∈N′(s′)such that for allx′∈X′,there is anx∈Xsuch thatxZx′;
(c-m-Zag)ifX′∈N′(s′),then there existsX∈N(s)such that for allx∈X,there is anx′∈X′such thatxZx′.
(M,s)and(M′,s′)is said to bec-monotonic bisimilar,writtens′),if there is ac-monotonic bisimulation betweenMandM′such thatsZs′.
Note that both monotonicc-bisimulation andc-monotonic bisimulation are defined between monotonic,c-models.
Proposition 7Everyc-monotonic bisimulation is a monotonicc-bisimulation.
ProofSuppose thatZis ac-monotonic bisimulation betweenMandM′,both of which are monotonic,c-models,to show thatZis also a monotonicc-bisimulation betweenMandM′.For this,assume thatsZs′,it suffices to show the condition(ii).
Assume that(U,U′)isZ-coherent.IfU∈N(s),by(c-m-Zig),there existsX′∈N′(s′)such that for allx′∈X′,there is ax∈Usuch thatxZx′.By assumption andx∈UandxZx′,we havex′∈U′,thusX′⊆U′.Then by(s)andX′∈N′(s′),we conclude thatU′∈N′(s′).The converse is similar,but by using(c-m-Zag)instead. □
Proposition 8Every monotonicc-bisimulation is ac-monotonic bisimulation.
ProofSuppose thatZis a monotonicc-bisimulation betweenMandM′,both of which are monotonic,c-models,to show thatZis also ac-monotonic bisimulation betweenMandM′.For this,given thatsZs′,we need to show the condition(c-m-Zig)and(c-m-Zag).We show(c-m-Zig)only,since(c-m-Zag)is similar.
Assume thatX∈N(s),defineX′={x′|xZx′for somex∈X}.It suffices to show thatX′∈N′(s′).The proof is as follows:by assumption and monotonicity ofM,we haveS∈N(s),then by(c),∅∈N(s).Since(∅,∅)isZ-coherent,by(ii),we infer∅∈N′(s′).From this and monotonicity ofM′,it follows thatX′∈N′(s′),as desired.□
As a corollary,the aforementioned two ways enable us to get the same bisimulation notion.
Corollary 3The notion of monotonicc-bisimulation is equal to the notion ofc-monotonic bisimulation.
So we can choose either of the two bisimulation notions to refer to the notion of bisimulation of CL over monotonic,c-models.In the sequel,we choose the simpler one,that is,monotonicc-bisimulation.One may easily see that this notion is stronger than monotonic bisimulation(for ML).
Similar to the case forc-bisimulation in Sec.4,we can show that
Proposition 9LetMandM′be monotonic,c-models,s∈Mands′∈M′.Ifthen for all
Theorem 3(Hennessy-Milner Theorem for monotonicc-bisimulation)LetMandM′be monotonic,∆-saturatedc-models,s∈Mands′∈M′.If for allφ∈L∆,M,s⊪
Similarly,we can define regularc-bisimulation,which is obtained by adding the property(i)intomonotonicc-bisimulation,and show the corresponding Hennessy-Milner Theorem.We omit the details due to space limitation.
6 Quasi-filter structures
We define a class of structures,called ‘quasi-filter structures’.6Note that our notion of quasi-filter is different from that in[2,p.215],where quasi-filter is defined as(s)+(i).For example,the latter notion is not necessarily closed under complements.
Definition 10(Quasi-filter frames and models) A neighborhood frameF=⟨S,N⟩is aquasi-filter frame,ifforalls∈S,N(s)possesses the properties(n),(i),(c),and(ws),where(ws)means being closed under supersets or co-supersets:for allX,Y,Z⊆S,X∈N(s)impliesX∪Y∈N(s)or(SX)∪Z∈N(s).
We say a neighborhood model is aquasi-filter model,if its underlying frame is a quasi-filter frame.
Note that in the above definition,the property(n)can be replaced with the property of“N(s)being nonempty”;in symbol,N(s)̸=∅.
The main result of this section is the following:for CL,every Kripke model has a pointwise equivalent quasi-filter model,butnotvice versa.
Definition 11(qf-variation) LetM=⟨S,R,V⟩is a Kripke model.qf(M)is said to be aqf-variationofM,ifqf(M)=⟨S,qfN,V⟩,where for anys∈S,qfN(s)={X⊆S:for anyt,u∈S,ifsRtandsRu,then(t∈Xiffu∈X)}.
The definition ofqfNis also quitenatural,sincejustas“for anyt,u∈S,ifsRtandsRu,then(t∈Xiffu∈X)”corresponds to the Kripke semantics of∆,X∈qfN(s)corresponds to the new neighborhood semantics of the operator,as will be seen more clearly in Prop.10.Note that the definition ofqfNcan be simplified as follows:

It is easy to see that every Kripke model has a(sole)qf-variation.We will demonstrate that,every such qf-variation is a quasi-filter model.
The following proposition states that every Kripke model and its qf-variation are pointwise equivalent.
Proposition 10LetM=⟨S,R,V⟩be a Kripke model.Then for allφ∈L∆,for alls∈S,we haveM,s⊨φ⇐⇒qf(M),s⊪φ,i.e.,φM⊨=φqf(M),whereφM⊨={t∈S|M,t⊨φ}.
ProofBy induction onφ.The nontrivial case is∆φ.
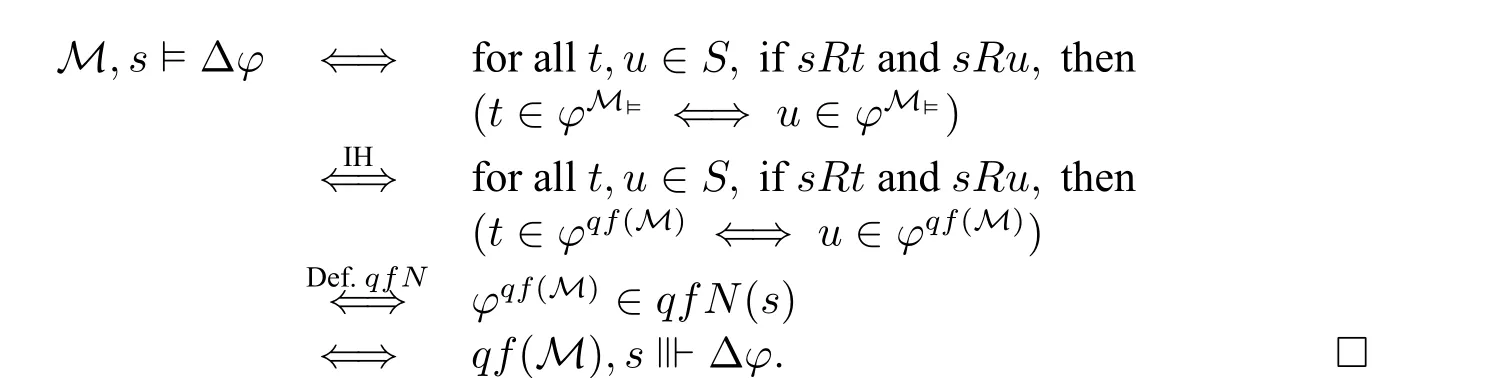
Proposition 11LetMbe a Kripke model.Thenqf(M)is a quasi-filter model.
ProofLetM=⟨S,R,V⟩.For anys∈S,we show thatqf(M)has those four properties of quasi-filter models.
(n):it is clear thatS∈qfN(s).
(i):assume thatX,Y∈qfN(s),we showX∩Y∈qfN(s).By assumption,for alls,t∈S,ifsRtandsRu,thent∈Xiffu∈X,and for alls,t∈S,ifsRtandsRu,thent∈Yiffu∈Y.Therefore,for allt,u∈S,ifsRtandsRu,we have thatt∈X∩Yiffu∈X∩Y.This entailsX∩Y∈qfN(s).
(c):assume thatX∈qfN(s),to showSX∈qfN(s).By assumption,for alls,t∈S,ifsRtandsRu,thent∈Xiffu∈X.Thus for alls,t∈S,ifsRtandsRu,thent∈SXiffu∈SX,i.e.,SX∈qfN(s).
(ws):assume,for a contradiction,that for someX,Y,Z⊆Sit holds thatX∈qfN(s)butX∪Y/∈qfN(s)and(SX)∪Z/∈qfN(s).W.l.o.g.we assume that there aret1,u1such thatsRt1,sRu1andt1∈X∪Ybutu1/∈X∪Y,and there aret2,u2such thatsRt2,sRu2andt2/∈(SX)∪Zbutu2∈(SX)∪Z.Thent2∈Xandu1/∈X,which is contrary to the fact thatX∈qfN(s)andsRu1,sRt2.□
The following result is immediate by Props.10 and 11.
Corollary4ForCL,every Kripke model has a pointwise equivalent quasi-filter model.
However,for CL,not every quasi-filter model has a pointwise equivalent Kripke model.The point is that quasi-filter models may not be closed underinfinite(i.e.arbitrary)intersections(see the property(r)in Def.1).
Proposition 12For CL,there is a quasi-filter model that has no pointwise equivalent Kripke model.
ProofConsider an infinite modelM=⟨S,N,V⟩,where
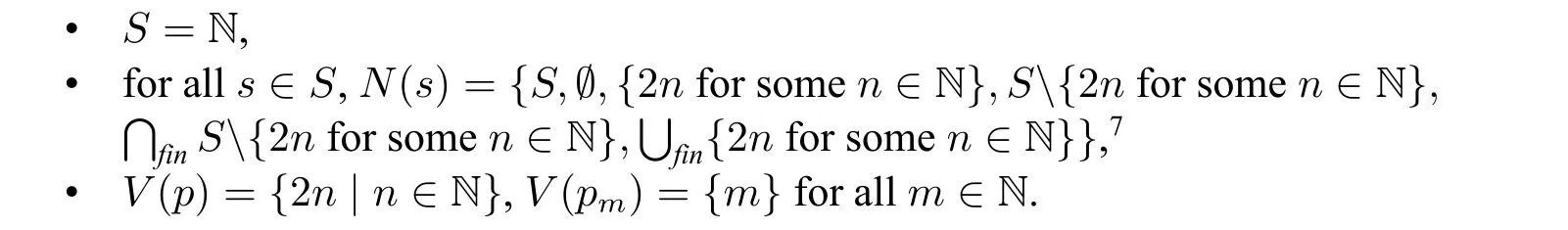
7{2n for some n∈N}denotes the union of finitely many sets of the form{2n for some n∈N},e.g.{0}∪{2}∪{4}.
It is not hard to check thatMis a quasi-filter model.8To verify(ws),we need only show the nontrivial caseFor this,we show a stronger result:for allThe cases for Z=S or Z=∅are clear.For other cases,we partition the elements in Z nto three disjoint(possibly empty)parts:odd numbers,even numbers in even numbers inNote that the first and third parts all belong;moreover,the union of the second part andis also in N(s).Note that for alls∈S,pM/∈N(s),thusIn particular
Suppose that there is a pointwise equivalent Kripke modelM′,thenThus there must be 2mand 2n+1 that are accessible from 0,wherem,n∈N.Since
However,when we restrict quasi-filter models to finite cases,the situation will be different.
Proposition 13For every finite quasi-filter modelM,there exists a pointwise equivalent Kripke modelM′,that is,for allφ∈L∆,for all worldss,M′,s⊨φ⇐⇒M,s⊪
ProofLetM=⟨S,N,V⟩be a finite quasi-filter model.DefineM′=⟨S,R,V⟩,whereRis defined as follows:for anys,t∈S,
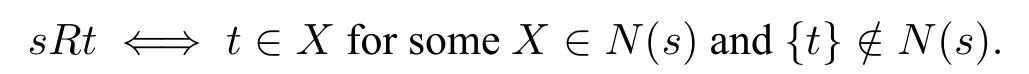
We will show that for allφ∈L∆and alls∈S,we have that

The proof proceeds with induction onφ∈L∆.The nontrivial case is∆φ,that is to show,M′,s⊨∆φ⇐⇒M,s⊪∆φ.
“⇐=:”Suppose,for a contradiction,thatM,s⊪ ∆φ,butM′,s⊭ ∆φ.ThenφM∈N(s),and there aret,u∈Ssuch thatsRtandsRuandM′,t⊨φandM′,u⊭φ.SinceφM∈N(s),by(c),we getSφM∈N(s);moreover,by(ws),we obtain thatφM∪{u}∈N(s)orSφM∪{t}∈N(s).IfφM∪{u}∈N(s),then bySφM∈N(s)and(i),we derive that(φM∪{u})∩SφM∈N(s),i.e.,{u}∩SφM∈N(s),by induction hypothesis,{u}={u}∩SφM∈N(s),contrary tosRuand the definition ofR.IfSφM∪{t}∈N(s),similarly we can show that{t}∈N(s),contrary tosRtand the definition ofR.
“=⇒:”Suppose thatto show thatthat is,there aret,u∈Ssuch thatsRt,sRuandM′,t⊨φandM′,u⊨¬φ.By supposition,φM/∈N(s).We show that there is at∈φMsuch that{t}/∈N(s)as follows:if not,i.e.,for allt∈φMwe have{t}∈N(s),then by(c),we getS{t}∈N(s),and using(i)we obtainviz.SφM∈N(s).9Since M is finite,we need only use the property that N is closed under finite intersections,which is equivalent to the property(i).This is unlike the case in Prop.12.Therefore using(c)again,we conclude thatφM∈N(s),which contradicts with the supposition.
Therefore,there is at∈φMsuch that{t}/∈N(s).Sincet∈SandS∈N(s)(by(n)),by the definition ofR,it follows thatsRt;furthermore,fromt∈φMand induction hypothesis,it follows thatM′,t⊨φ.
Similarly,we can show that there is au∈(¬φ)Msuch that{u}/∈N(s).ThussRuandM′,u⊨¬φ,as desired. □
In spite of Prop.12,as we shall see in Coro.5,logical consequence relations over Kripke semantics and over the new neighborhood semantics on quasi-filter models coincide with each other for CL.
7 qf-Bisimulation
This section proposes the notion of bisimulation for CL over quasi-filter models,called ‘qf-bisimulation’.The intuitive idea of the notion is similar to monotoniccbisimulation andc-bisimulation,i.e.the notion of precocongruences with particular properties(in the current setting,those four properties of quasi-filter models).
Definition 12(qf-bisimulation)LetM=⟨S,N,V⟩andM′=⟨S′,N′,V′⟩be quasifilter models.A nonempty relationZ⊆S×S′is aqf-bisimulationbetweenMandM′,if for all(s,s′)∈Z,
(qi)s∈V(p)iffs′∈V′(p)for allp∈Prop;
(qii)if the pair(U,U′)isZ-coherent,thenU∈N(s)iffU′∈N′(s′).
We say(M,s)and(M′,s′)areqf-bisimilar,writtenif there is a qf-bisimulationZbetweenMandM′such that(s,s′)∈Z.
Note that the notion ofqf-bisimulation is defined between quasi-filter models.It is clear that every qf-bisimulation is ac-bisimulation,but it is not necessarily a monotonicc-bisimulation,since it is easy to find a quasi-filter model which is not closed under supersets.
Analogous to the case forc-bisimulation in Sec.4,we can show that
Proposition 14LetM,M′be both quasi-filter models,s∈M,s′∈M′.If(M,s)then for all
Theorem 4(Hennessy-Milner Theorem for qf-bisimulation)LetMandM′be∆-saturated quasi-filter models,ands∈M,s′∈M′.If for allφ∈L∆,M,s⊪φ⇐⇒
We conclude this section with a comparison between the notion of qf-bisimulation and that of rel-∆-bisimulation in[1,Def.6].
Definition 13(rel-∆-bisimulation) LetM=⟨S,R,V⟩andM′=⟨S′,R′,V′⟩be Kripke models.A nonempty relationZ⊆S×S′is arel-∆-bisimulationbetweenMandM′,if for all(s,s′)∈Z,
(Atoms)s∈V(p)iffs′∈V′(p)for allp∈Prop;
(Coherence)if the pair(U,U′)isZ-coherent,then
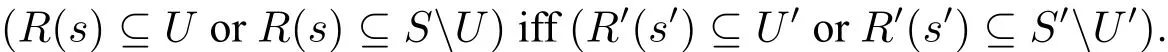
We say(M,s)and(M′,s′)arerel-∆-bisimilar,writtenif there is a rel-∆-bisimulationZbetweenMandM′such that(s,s′)∈Z.
The result below asserts that every rel-∆-bisimulation between Kripke models can be transformed to a qf-bisimulation between quasi-filter models.
Proposition 15LetM=⟨S,R,V⟩andM′=⟨S′,R′,V′⟩be Kripke models.IfZis a rel-∆-bisimulation betweenMandM′,thenZis a qf-bisimulation betweenqf(M)andqf(M′).
ProofSupposeZisarel-∆-bisimulation betweenMandM′.ByProp.11,qf(M)andqf(M′)are both quasi-filter models.It suffices to show thatZsatisfies the two conditions of a qf-bisimulation.For this,assume that(s,s′)∈Z.(qi)is clear from(Atoms).
For(qii):let(U,U′)beZ-coherent.We have the following line of argumentation:U∈qfN(s)iff(by definition ofqfN)(R(s)⊆UorR(s)⊆SU)iff(by Coherence)(R′(s′)⊆U′orR′(s′)⊆S′U′)iff(by definition ofqfN′)U′∈qfN′(s′). □
In the current stage,we do not know whether every qf-bisimulation between quasifilter models can be transformed to a rel-∆-bisimulation between Kripke models.Note that this is important,since if it holds,then we can see clearly the essence of rel-∆-bisimulation,i.e.precocongruences with those four quasi-filter properties.We leave it for future work.
8 Frame definability
Recall that under the old neighborhood semantics,all the ten neighborhood properties in Def.1are undefinable inL∆.In contrast,under the new semantics,almost all these properties are definable in the same language.The following witnesses the properties and the corresponding formulas defining them.Recall that(c)is the minimal condition of neighborhood frames.

Proposition16The right-hand formulas define the corresponding left-hand properties.
ProofBy Prop.1,∆p↔∆¬pdefines(c).For other properties,we take(d)and(b)as examples,which resort to the property(c).Given anyc-frameF=⟨S,N⟩.
Suppose thatFhas(d),to show thatF⊪∇p.Assume,for a contradiction that there is a valuationVonF,ands∈S,such thatwhereM=⟨F,V⟩.ThenpM∈N(s).On the one hand,by supposition,SpM/∈N(s);on the other hand,by(c),SpM∈N(s),contradiction.Conversely,assume thatFdoes not have(d),to show thatF̸⊪∇p.By assumption,there is anXsuch thatX∈N(s)andSX∈N(s).Define a valuationVonFsuch thatV(p)=X,and letM=⟨F,V⟩.ThuspM∈N(s),i.e.,M,s⊪ ∆p,and hence
SupposeFhas(b),to showF⊪p→∆∇p.For this,given anyM=⟨S,N,V⟩ands∈S,assume thatM,s⊪p,thens∈pM.By supposition,{u∈S|SpM/∈N(u)}∈N(s).By(c),this is equivalent to that{u∈S|pM/∈N(u)}∈N(s),i.e.,{u∈S|M,u⊪∇p}∈N(s),viz.,(∇p)M∈N(s),thusM,s⊪ ∆∇p.Conversely,supposeFdoes not have(b),to showBy supposition,there is ans∈SandX⊆S,such thats∈Xand{u∈S|SX/∈N(u)}/∈N(s).Define a valuationVonFsuch thatV(p)=X,and letM=⟨F,V⟩.ThenM,s⊪p,and{u∈S|SpM/∈N(u)}/∈N(s).By(c)again,this means that{u∈S|pM/∈N(u)}/∈N(s),that is,{u∈S|M,u⊪∇p}/∈N(s),i.e.,(∇p)M/∈N(s),thereforeM,s∆∇p. □
The following result will be used in the next section.
Proposition 17∆p→∆(p→q)∨∆(¬p→r)defines the property(ws),where(ws)is as defined in Def.10.
ProofLetF=⟨S,N⟩be a neighborhood frame.
First supposeFhas(ws),we need to showF⊪∆p→∆(p→q)∨∆(¬p→r).For this,assume for any modelMbased onFands∈SthatM,s⊪∆p.ThenpM∈N(s).By supposition,pM∪rM∈N(s)or(¬p)M∪qM∈N(s).The former implies(¬p→r)M∈N(s),thusM,s⊪ ∆(¬p→r);the latter implies(p→q)M∈N(s),thusM,s⊪ ∆(p→q).Either case impliesM,s⊪ ∆(p→q)∨∆(¬p→r),henceM,s⊪∆p→∆(p→q)∨∆(¬p→r).ThereforeF⊪∆p→∆(p→q)∨∆(¬p→r).
Conversely,supposeFdoes not have(ws),we need to showF̸⊪ ∆p→∆(p→q)∨∆(¬p→r).From the supposition,it follows that there areX,YandZsuch thatX∈N(s),X⊆YandY/∈N(s),SX⊆ZandZ/∈N(s).DefineVas a valuation onFsuch thatV(p)=X,V(q)=ZandV(r)=Y.SincepM=V(p)∈N(s),we haveM,s⊪∆p.SinceX⊆Y,(¬p→r)M=X∪Y=Y/∈N(s),thusM,∆(¬p→r).SinceSX⊆Z,(p→q)M=(SX)∪Z=Z/∈N(s),and thusM,s∆(p→q).HenceM,s∆p→∆(p→q)∨∆(¬p→r),and thereforeF̸⊪ ∆p→∆(p→q)∨∆(¬p→r). □
Note that in the above proposition,we do not use the property(c),that is to say,it holds for the class of all neighborhood frames.
9 Axiomatizations
This section presents axiomatizations ofL∆over various classes of frames.The minimal system E∆consists of the following axiom schemas and inference rule.

Note that E∆is the same as CCL in[4,Def.7].Recall that(c)is the minimal neighborhood property.
Theorem 5E∆is sound and strongly complete with respect to the class ofc-frames.
ProofImmediate by the soundness and strong completeness of E∆w.r.t.the class of all neighborhood frames under⊩[4,Thm.1]and Coro.1. □
Now consider the following extensions of E∆,which are sound and strongly complete with respect to the corresponding frame classes.We omit the proof detail since it is straightforward.

notation axioms systems frame classes∆M ∆(φ∧ψ)→∆φ∧∆ψ M∆=E∆+∆M cs∆C ∆φ∧∆ψ→∆(φ∧ψ)R∆=M∆+∆C csi
One may ask the following question:is R∆+∆⊤sound and strongly complete with respect to the class of filters,i.e.the frame classes possessing(s),(i),(n)?The answer is negative,since the soundness fails,although it is indeed sound and strongly complete with respect to the class of filters satisfying(c).
Now consider the following axiomatization K∆,which is provably equivalent to CL in[5,Def.4.1].
Definition 14(Axiomatic system K∆) The axiomatic system K∆is the extension of E∆plus the following axiom schemas:
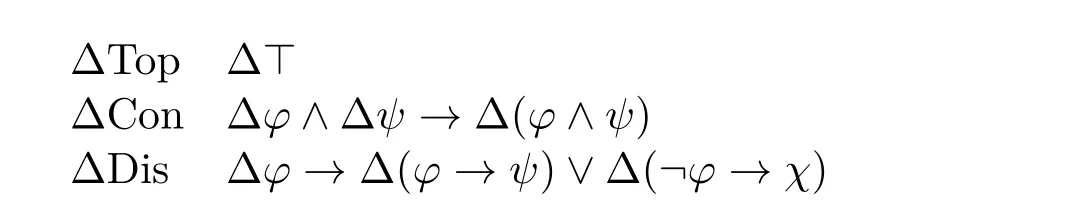
Theorem 6K∆is sound and strongly complete with respect to the class of quasi-filter frames.
ProofSoundness is immediate by frame definability results of the four axioms.
For strong completeness,since every K∆-consistent set is satisfiable in a Kripke model(cf.e.g.[5]),by Coro.4,every K∆-consistent is satisfiable in a quasi-filter model,thus also satisfiable in a quasi-filter frame. □
Note that the strong completeness of E∆and of K∆can be shown directly,by defining the canonical neighborhood functionNc(s)={|φ||∆φ∈s}.
As claimed at the end of Sec.6,for CL,although not every quasi-filter model has a pointwise equivalent Kripke model,logical consequence relations over Kripke semantics and over the new neighborhood semantics on quasi-filter models coincide with each other.Now we are ready to show this claim.
Corollary 5The logical consequence relations⊪qfand⊨coincide for CL.That is,for all Γ∪{φ}⊆L∆,Γ ⊪qfφ⇐⇒Γ⊨φ,where,by Γ ⊪qfφwe mean that,for every quasi-filter modelMandsinM,ifM,s⊪ Γ,thenM,s⊪φ.Therefore,for allφ∈L∆,⊪qfφ⇐⇒⊨φ,i.e.,the new semantics over quasi-filter models has the same logic(valid formulas)on CL as the Kripke semantics.
ProofBy the soundness and strong completeness of K∆with respect to the class of all Kripke frames(cf.e.g.[5]),Γ⊢K∆φiff Γ ⊨φ.Then using Thm.6,we have that Γ ⊩qfφiff Γ ⊨φ. □
10 Conclusion and Discussions
In this paper,we proposed a new neighborhood semantics for contingency logic,which simplifies the original neighborhood semantics in[4]but keeps the logic the same.This new perspective enables us to define the notions of bisimulation for contingency logic over various model classes, one of which can help us understand the essence of nbh-Δ-bisimulation, and obtain the corresponding Hennessy-Milner Theorems, in a relatively easy way.Moreover,we showed that for this logic,almost all the ten neighborhood properties,which are undefinable under the old semantics,are definable under the new one.And we also had some simple results on axiomatizations.Besides,under the new semantics,contingency logic has the same expressive power as standard modal logic.It also gives us a neighborhood perspective that necessity is amount to non-contingency plus the property(c).We conjecture that our method may apply to other non-normal modal logics,such as logics of unknown truths and of false beliefs.We leave it for future work.
Another future work would be axiomatizations of monotonic contingency logic and regular contingency logic under the old neighborhood semantics. Note that our axiomatizations M∆and R∆are not able to be transformed into the corresponding axiomatizations under the old semantics, since our underlying frames arec-frames.For example,although we do have⊪cs∆(φ∧ψ)→∆φ∧∆ψ,we donothave⊩s∆(φ∧ψ)→∆φ∧∆ψ;consequently,although M∆is sound and strongly complete with respect to the class ofcs-frames under the new neighborhood semantics,it isnotsound with respect to the class ofs-frames under the old one.Thus the axiomatizations of these logics under the old neighborhood semantics are still open.10Update:These two open questions were raised in[1]and have been answered in[3].

