九句因理论的形式语义学

许春梅

中国社会科学院世界宗教研究所

adai159099@126.com

1 背景介绍

近代以来，西学东渐，西方逻辑（特别是形式逻辑）被系统地引荐到中国，引入到因明的研究中。以西方逻辑研究因明成了汉地因明研究的主流。关于陈那论师的九句因、因三相等等理论，学者们自觉不自觉地运用了欧拉图、三段论、谓词逻辑等等方法对其进行分析。比如，沈剑英先生在《因明正理门论译解》一书中运用欧拉图的分析方法研究九句因理论。（[3]，第50–58页）郑伟宏先生在《佛家逻辑通论》一书中运用三段论分析因三相理论，因喻符合因三相理论不能得定解。陈那的三支作法没有改变类比推理的性质（[5]，第80–86页）；巫寿康先生在《因明正理门论研究》一书中运用数理逻辑分析九句因理论、因三相理论内部存在的矛盾，并给出解决办法。（[4]，第3–21页）何嵘在其硕士论文《〈正理门论〉的认识论和逻辑体系研究》中运用谓词逻辑对因三相理论作形式化翻译，在坚持陈那的同、异品概念是除宗有法的这一初始假设下，发现因的后二相在保证共许因法和不共许宗法的不相离性上出现瑕疵，从而得出因三相理论不能必然推出结论的观点。（[1]，第13–24页）等等。学者们从不同的初始假设出发，运用西方逻辑，特别是形式逻辑分析分法，得出了不同的结论。至于何种初始假设更为契合陈那论师的原意，以及哪种西方逻辑分析方法更为得力等等问题，笔者将另撰文论述。

本文将为九句因理论的研究提供一个新的视角，即将其置于形式语义框架下，系统地对其进行刻画、翻译等研究工作。具体地，通过给出适合陈那论师关于同、异品及因等概念的初始假设。然后再在此语义框架下，再对九句因理论作翻译。从形式语义的角度来研究、理解九句因理论的本质和意义。

2 形式语义学

我们先给出一个适合陈那论师关于同、异品及因等概念的初始假设，即定义一个合适的语义框架。

定义1.（语义框架）：一个语义框架是一个三元组⟨A,T,B⟩，其中

其中，定义中的符号A表示我们的整个认知世界；符号T表示同品，符号T的余集表示异品；符号B表示因。

首先，由于共业和别业的关系，每个人的整个认知世界既有相似部分，又有不同的部分，但是无论如何，它都不可能是空白。因为我们总是在一定认知的基础上进行认知活动，并且不断地更新我们的认知世界。所以，代表认知世界的集合A必须是非空集，即“A≠∅”。

其次，根据陈那论师所定义的同、异品之间是一种矛盾关系，我们就可以用同品T的余集来表示异品，根据集合论，这样就有用这种形式刻画可以更清楚地表达同、异品之间的关系：同、异品是一对具有矛盾关系的概念，它们的并集是我们的整个认知世界。

第三，陈那论师所定义的同、异品这两个初始概念是根据宗后陈属性界定的，一旦宗支给出，它的宗后陈也就已经确定了，所以，表示同品的集合T不可能是空集，即“T≠∅”。而且同品一定是在我们认知世界里的，如不然，我们如何实现在整个认知世界之外自由地思维呢？这是难以想象的。但是，为什么同品不可以是我们的整个认知世界呢？如此，我们整个认知世界里所有一切全都具有同品的属性（即宗后陈的属性），这就违背了立宗必须不顾论宗，随自意立的原则。所以，同品必须是整个认知世界的一部分，即“T⊂A”。再根据集合论，由于所以，故而，不必再讨论“异品非空”，定义1不需另外再定义

最后，根据陈那论师的九句因理论，第五句因中的因是空概念，剩余的其它八句因中的因不是空概念，所以，将表示因的集合B定义为“B⊆A”是合适的。这个定义的意思是：因概念不超出我们的认知世界，但它可以是空概念。

综上所述，定义1这个语义框架适合陈那因明中关于同、异品，以及因这三个概念的定义。

3 形式语义翻译

本节的工作就是在定义1这个语义框架下，对九句因理论作形式语义翻译。

首先，因与同品、异品的关系，各有四种情况，即对于同、异品来说，全部有因性、全部没有因性、部分有因性以及部分没有因性。我们先将每一种情况，都进行了相应的形式语义翻译。然后，再用欧拉图直观呈现其翻译所表达的意思。记号说明：大方框表示全集A，小方框表示同品集“T”，剩余部分表示异品集阴影部分表示因的集合“B”。空白部分表示因的补集

因在同品中的各种情况及对应翻译一览表：

T1：全部同品都有因性，可译为“T⊆B”，具有如图1三种情况。

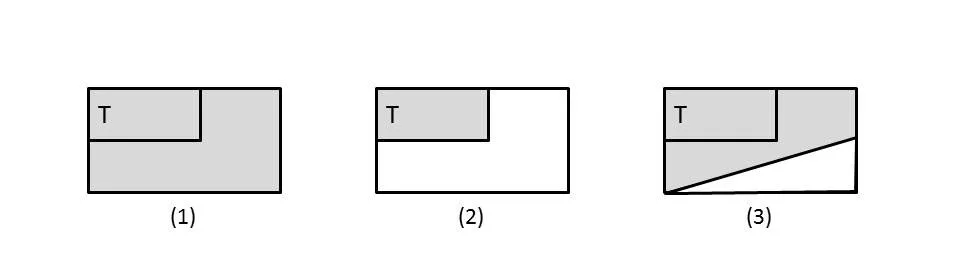
图1:全部同品都有因性

T2：全部同品没有因性，可译为“T∩B=∅”，具有如图2三种情况。

图2:全部同品没有因性

T3：部分同品具有因性，可译为具有如图3三种情况；T4：部分同品没有有因性，可译为具有如图4三种情况。

图3:部分同品具有因性

图4:部分同品没有有因性

如上所示，虽然T3与T4所表示的意义不同，但是它们的欧拉图是一样的。归根结底，这是因为陈那论师将全部与部分严格区分，以及他对同、异品这两个初始概念的特殊定义所致。陈那论师将这两种情况合并为一，就是“又（因）于同品有、无、及彼俱二”（[2]，第170–175页）中的“彼俱二”，意思是说部分同品有因性，部分同品没有因性。根据T3与T4所反映的欧拉图是相同的，说明陈那论师的这种做法并无不妥。因此，也可称因与同品具有三种关系，分别是全部同品有因性、全部同品没有因性和部分同品有因性、部分同品没有因性。

因在异品中的各种情况及对应翻译一览表

1：全部异品都有因性，可译为具有如图5三种情况。

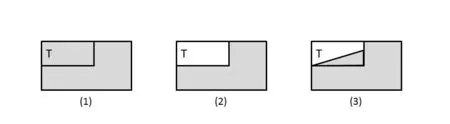
图5:全部异品都有因性

2：全部异品没有因性，可译为具有如图6三种情况。

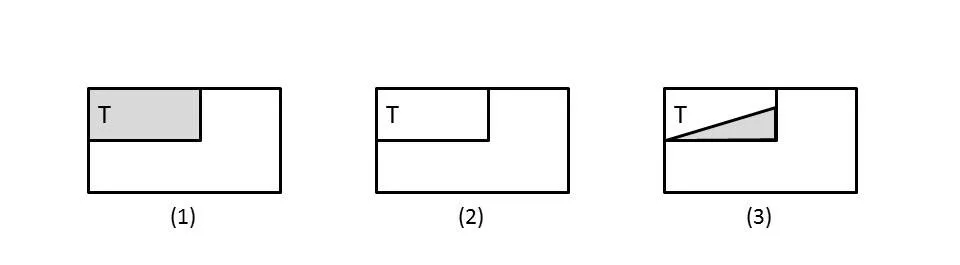
图6:全部异品没有因性

3：部分异品具有因性，可译为具有如图 7 三种情况。

图7:部分异品具有因性

4：部分异品没有有因性，可译为具有如图 8 三种情况。

图8:部分异品没有有因性

其次，将因在同品中的情况一一地与在异品中的每一种情况组合起来，并对其进行了相应的形式语义翻译。然后，再用欧拉图直观呈现其翻译后所表达的意义。为了说明方便，用记号表示因在同品的第m种情况与因在异品中的第n种情况的组合。例如，表示因在同品的第1种情况与因在异品中的第1种情况的组合，其意为：全部同品都有因性，且全部异品都有因性。

(T11)：全部同品有因性，且全部异品有因性。这就是九句因的第一句因，它可译为等价于“A=B”。根据“全部异品有因性”，就排除了T1：(2)和T1：(3)，剩下T1：(1)。再根据“全部同品有因性”，就排除了：(3)，剩下见图 9。

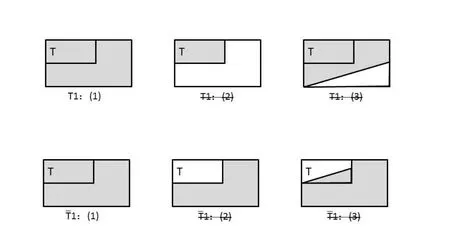
图9:全部同品有因性，且全部异品有因性

基于上述操作，我们可以做这样的总结：

总结1九句因的第一句：全部同品都有因性，且全部异品都有因性。可译为等价于“A=B”。如果用欧拉图表示就如图10。

图10:全部同品都有因性，且全部异品都有因性

（T1，）：全部同品有因性，且全部异品没有因性。这就是九句因的第二句因，它可译为等价于“T=B”。根据“全部异品没有因性”，就排除了T1：(1)和T1：(3)，剩下T1：(2)。再根据“全部同品有因性”，就排除了剩下如图 11。

基于上述操作，我们可以做这样的总结：

总结2九句因的第二句：全部同品有因性，且全部异品没有因性。可译为等价于“T=B”。如果用欧拉图表示就如图12。

（T1，）：全部同品有因性，且部分异品有因性。这就是九句因的第三句因，它可译为等价于“T⊂B”。根据“部分异品有因性”，就排除了T1：(1)和T1：(2)，剩下T1：(3)。再根据“全部同品有因性”，就排除了和剩下如图 13。

图11:全部同品有因性，且全部异品没有因性

图12:全部同品有因性，且全部异品没有因性

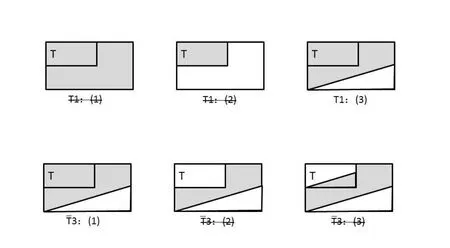
图13:全部同品有因性，且部分异品有因性

基于上述操作，我们可以做这样的总结：

总结3九句因的第三句：全部同品都有因性，且部分异品有因性。可译为等价于“T⊂B”。如果用欧拉图表示就如图14。

图14:全部同品有因性，且部分异品有因性

（T1，）：全部同品有因性，且部分异品没有因性。它可译为“(T⊆B)∧((T∩B̸=∅)∧(T≠B))”，等价于“T⊂B”。根据“部分异品没有因性”，就排除了T1：(1)和T1：(2)，剩下T1：(3)。再根据“全部同品有因性”，排除了(2)和剩下如图 15。

图15:全部同品有因性，且部分异品没有因性

基于上述操作，我们可以做这样的总结：

总结4全部同品有因性，且部分异品没有因性。可译为等价于“T⊂B”。如果用欧拉图表示就如图16。

图16:全部同品有因性，且部分异品没有因性

（T2，）：全部同品没有因性，且全部异品有因性。这就是九句因的第四句因，它可译为等价于根据“全部异品有因性”，就排除了T2：(2)和T2：(3)，剩下T2：(1)。再根据“全部同品没有因性”，排除了和，剩下如图 17。

图17:全部同品没有因性，且全部异品有因性

基于上述操作，我们可以做这样的总结：

总结5九句因的第四句：全部同品没有因性，且全部异品都有因性。可译为等价于如果用欧拉图表示就如图18。

图18:全部同品没有因性，且全部异品都有因性

（T2，）：全部同品没有因性，且全部异品没有因性。这就是九句因的第五句因，它可译为等价于“B=∅”。根据“全部异品没有因性”，就排除了T2：(1)和T2：(3)，剩下T2：(2)。再根据“全部同品没有因性”，就排除了和剩下如图 19。

基于上述操作，我们可以做这样的总结：

总结6九句因的第五句：全部同品没有因性，且全部异品没有因性。可译为等价于“B=∅”。如果用欧拉图表示就如图20。

（T2，T3）：全部同品没有因性，且部分异品有因性。这就是九句因的第六句因，它可译为等价于。根据“部分异品有因性”就排除了T2：(1)和T2：(2)，剩下T2：(3)。再根据“全部同品没有因性”，就排除了剩下如图 21。

基于上述操作，我们可以做这样的总结：

总结7九句因的第六句：全部同品没有因性，且部分异品有因性。可译为如果用欧拉图表示就如图22。

（T2，）：全部同品没有因性，且部分异品没有因性。它可译为“(T∩B=等价于“B⊂T”。根据“部分异品没有因性”，就排除了T2：(1)和T2：(2)，剩下T2：(3)。再根据“全部同品没有因性”，排除了剩下如图 23。

图19:全部同品没有因性，且全部异品没有因性

图20:全部同品没有因性，且全部异品没有因性

图21:全部同品没有因性，且部分异品有因性

图22:全部同品没有因性，且部分异品有因性

图23:全部同品没有因性，且部分异品没有因性

基于上述操作，我们可以做这样的总结：

总结8全部同品没有因性，且部分异品没有因性。可译为等价于“B⊂T”。如果用欧拉图表示就如图24。

图24:全部同品没有因性，且部分异品没有因性

（T3，T1）：部分同品有因性，且全部异品有因性。这就是九句因的第七句因，它可译为等价于根据“全部异品有因性”，就排除了T3：(2)和T3：(3)，剩下T3：(1)。再根据“部分同品有因性”，排除了如图 25。

基于上述操作，我们可以做这样的总结：

总结9九句因的第七句：部分同品有因性，且全部异品有因性。可译为“((T∩等价于如果用欧拉图表示就如图26。

图25:部分同品有因性，且全部异品有因性

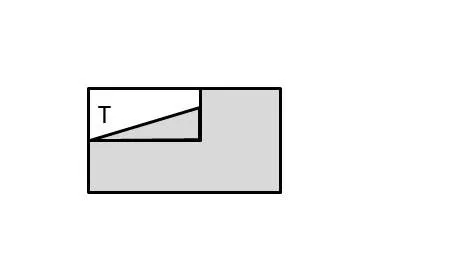
图26:部分同品有因性，且全部异品有因性

（T3，2）：部分同品有因性，且全部异品没有因性。这就是九句因的第八句因，它可译为等价于“B⊂T”。根据“全部异品没有因性”，就排除了T3：(1)和T3：(3)，剩下T3：(2)。再根据“部分同品有因性”，排除了如图 27。

图27:部分同品有因性，且全部异品没有因性

基于上述操作，我们可以做这样的总结：

总结10九句因的第八句：部分同品有因性，且全部异品没有因性。可译为等价于“B⊂T”。如果用欧拉图表示就如图28。

图28:部分同品有因性，且全部异品没有因性

（T3，3）：部分同品有因性，且部分异品有因性。这就是九句因的第九句因，它可译为根据“部分异品有因性”，就排除了T3：(1)和T3：(2)，剩下T3：(3)。再根据“部分同品有因性”，排除了如图 29。

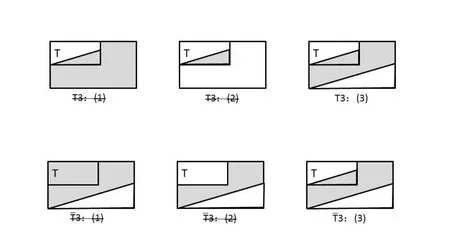
图29:部分同品有因性，且部分异品有因性

基于上述操作，我们可以做这样的总结：

总结11九句因的第九句：部分同品有因性，且部分异品有因性。可译为“((T∩如果用欧拉图表示就如图30。

图30:部分同品有因性，且部分异品有因性

（T3，4）：部分同品有因性，且部分异品没有因性。它可译为“((T∩B≠根据“部分异品没有因性”，就排除了T3：(1)和T3：(2)，剩下T3：(3)。再根据“部分同品有因性”，排除了和剩下如图 31。

图31:部分同品有因性，且部分异品没有因性

基于上述操作，我们可以做这样的总结：

总结12部分同品有因性，且部分异品没有因性。可译为如果用欧拉图表示就如图32。

图32:部分同品有因性，且部分异品没有因性

（T4，1）：部分同品没有因性，且全部异品有因性。它可译为等价于根据“全部异品有因性”，就排除了T4：(2)和T4：(3)，剩下T4：(1)。再根据“部分同品没有因性”，排除了(1)和剩下如图 33。

基于上述操作，我们可以做这样的总结：

总结13部分同品没有因性，且全部异品有因性。可译为，等价于如果用欧拉图表示就如图34。

（T4，T2）：部分同品没有因性，且全部异品没有因性。它可译为等价于“B⊂T”。根据“全部异品没有因性”，就排除了T4：(1)和T4：(3)，剩下T4：(2)。再根据“部分同品没有因性”，排除了和，剩下如图 35。

基于上述操作，我们可以做这样的总结：

图33:部分同品没有因性，且全部异品有因性

图34:部分同品没有因性，且全部异品有因性

图35:部分同品没有因性，且全部异品没有因性

总结14部分同品没有因性，且全部异品有因性。可译为“等价于“B⊂T”。如果用欧拉图表示就如图36。

（T4，部分同品没有因性，且部分异品有因性。它可译为根据“部分异品有因性”，就排除了T4：(1)和T4：(2)，剩下T4：(3)。再根据“部分同品没有因性”，排除了和剩下如图 37。

基于上述操作，我们可以做这样的总结：

图36:部分同品没有因性，且全部异品有因性

图37:部分同品没有因性，且部分异品有因性

总结15部分同品没有因性，且部分异品有因性。可译为如果用欧拉图表示就如图38。

图38:部分同品没有因性，且部分异品有因性

（T4，4）：部分同品没有因性，且部分异品没有因性。它可译为根据“部分异品没有因性”，就排除了T4：(1)和T4：(2)，剩下再根据“部分同品没有因性”，排除了T3：(1)和剩下如图 39。

基于上述操作，我们可以做这样的总结：

总结16部分同品没有因性，且部分异品没有因性。可译为如果用欧拉图表示就如图40。

图39:部分同品没有因性，且部分异品没有因性

图40:部分同品没有因性，且部分异品没有因性

表1:因在同、异品中的十六种情况及其对应翻译一览表

4 结论

通过对九句因理论作形式语义刻画这一工作，不难得出如下结论：

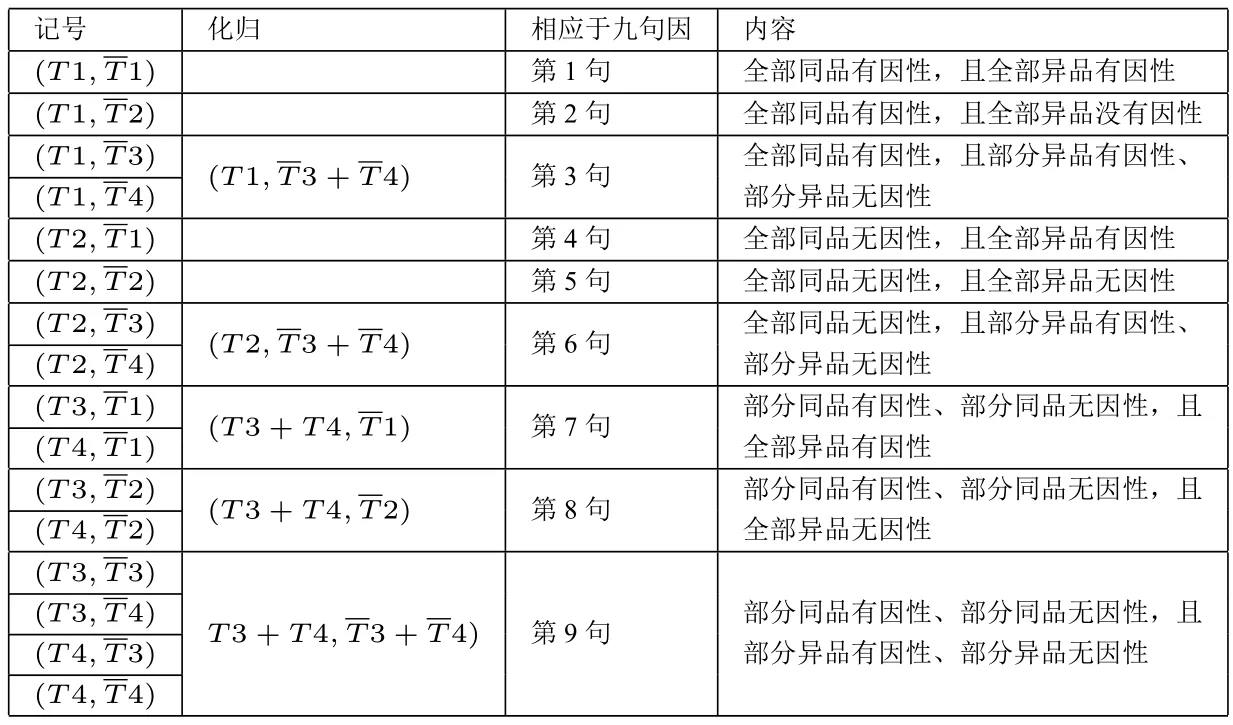
表2:因在同、异品中的十六种关系化归情况一览表

首先，九句因理论本质上是给出了关于两个“差别”（或词项）间外延关系探讨的一般方法。例如，在讨论声是否无常这一问题时，陈那论师的做法是以声的一个差别为中介，比如“所作性”，构建“同品”与“异品”这一对具有矛盾关系的概念，然后考察“所作性”与同、异品间的关系，由于同、异品是根据是否具有无常性来定义的，因此，也就是考察“所作性”分别与“无常”、“非无常”之间的关系。同理，任给两个词项都可以用这种方法探讨。这种探讨问题的方法已经完全跳脱具体内容上的探讨，已然上升到了逻辑的高度、形式化的高度。正是在这个意义上，可以说陈那论师的九句因理论具有划时代的里程碑式的意义，其工作完全可以与亚里士多德的逻辑工作相媲美。

其次，陈那论师的同、异品这一组概念在九句因理论中起到极为重要的作用，使得整个理论非常地简洁、直观。同、异品已不是古因明论师的用法，它有严格的用法，即同、异品是一对矛盾关系，它们共同组成了全集。不是同品，就是异品；反之亦然。找不到既不是同品，又不是异品的事物。在具体的操作上，同、异品是由宗后陈来定义的：凡具有宗后陈的属性就是同品，反之，不具有宗后陈属性的就是异品。其模型如图41：

图41:圆圈表示同品，方框以内圆圈以外表示异品，大方框表示全集

正是这个模型使得因与同、异品的关系是九种而不是更多，也不是更少。

最后，虽然本文并没有论证为什么只有满足第(2)、(8)句的因才是正因，但是通过形式语义的分析，还是不难直观地得到这个结论：只有当宗后陈的外延包含因性的外延时，这样的因才是正因。这就是因三相中的第二、三相。正是这个意义上说，九句因理论是因三相理论的基础、核心，也是构建三支作法中喻支的凭依。