如何避免贫乏性结果
刘吉宴
京都大学大学院文学研究科哲学研究室阳明大学心智哲学研究所
liuchiyen@gmail.com
1 前言
直陈条件句(indicative conditionals)的主观概率(subjective probability)该如何定义,是一直很受争议的问题。尽管如此,许多人认为它和条件概率(conditional probability)之间有着极为密切的关系。关于此点,一个在条件句的文献里最常被广泛讨论的主张是亚当斯(Ernest Adams)所提出的亚当斯论题(Adams’Thesis)。然而,亚当斯论题的明确意义究竟是什么仍需要进一步的厘清。所谓的直陈条件句是指“如果……,……”这类的语句,为便于讨论,文本以下便用A→B来表示直陈条件句。1笔者用“如果……,……”来代表直陈条件句,用“假如……,……”来代表虚拟条件句或反事实条件句,这样的区分参考自[28,30]。亚当斯当初主张:
对所有真值函数的句式φ和ψ,如果P(φ)̸=0,P(φ→ψ)=P(φ∧ψ)/P(φ),且如果P(φ)=0,P(φ→ψ)=1。([1],第 185 页)
以上的主张有两点值得注意,第一,在不考虑量化词和模态词的条件下,φ和ψ只能是由∧,∨,¬所组成的句式,因为亚当斯主张直陈条件句没有真假值。第二,亚当斯后来不再坚持P(φ)=0时,P(φ→ψ)=1,改称P(φ)=0时,P(φ→ψ)没有定义([2],第5页)。
由于在标准的概率理论中,

因此,后来亚当斯论题通常被表述如下:
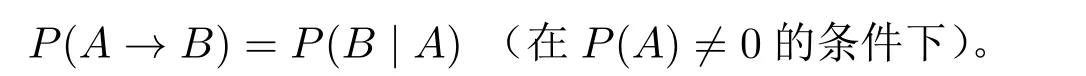
我们可以看到,上面等式的两边在形式上都以P,也就是“概率”来表示主观概率。大家对于等式右边的P(B|A)所代表的意思是没有争议的,问题在于,大家对于等式左边P(A→B)所谓的“概率”之解读存在着有很大的分歧。如上所述,亚当斯主张A→B并没有真假值,因此并不认为P(A→B)代表A→B“为真的”概率。
所以,为求公平,让我们先把亚当斯论题表述如下:

杰克森(Frank Jackson)认为,P∗(A→B)应被解读为A→B的可断言性(assertibility)([13]);亚当斯自己则是曾用可断说性(assertability)来指称P∗([1]),刘易士(David Lewis)和麦克德莫特(Michael McDermott)后来也认为P∗(A→B)应被解读为A→B的可断说性([19,22])。但是,亚当斯、刘易士、以及麦克德莫特对于什么是可断说性却有相当不同的看法。然而,刘易士对(AT)提出文献上著名的贫乏性结果(triviality results),刘易士指出,无论支持(AT)的人怎么解读其左边的P∗,只要他们承认P∗会遵守标准的概率法则,贫乏性结果就会出现([19,20])。
刘易士的贫乏性结果一开始来自于史东内克(Robert Stalnaker)提出的主张,史东内克认为A→B为真的概率应等同于P(B|A)([26])。2不过,由于贫乏性结果,史东内克后来已放弃这个想法,甚至提出一个他自己版本的贫乏性结果。([27])他这样的解读被称为“史东内克假说”(Stalnaker’s hypothesis),它和一开始的等式有同样的表述方式:

我们可以把(SH)当做是(AT)的一种解读方式,据此,我们可以把亚当斯论题和贫乏性结果之间的关系分成两大阵营。其中一个阵营认为直陈条件句有真假值,假如亚当斯论题是正确的主张,那么它应该被解读成(SH)。但由于贫乏性结果,(SH)不可能是对的主张;所以亚当斯论题不是正确的主张。另外一个阵营则是认为条件概率捕捉到直陈条件句一个很重要的面向,然而,贫乏性结果显示的是,条件概率不可能是直陈条件句为真的概率,(SH)是对亚当斯论题错误的解读方式;因此直陈条件句没有真假值。简言之,以上两个阵营都认为亚当斯论题、贫乏性结果和条件句有真假值这三者之间是不兼容的。由于贫乏性结果是牢不可破的,因此我们只能在亚当斯论题和条件句有真假值之间选一个立场支持。
本文的目标是要论证另一种不同于前述两种阵营的立场是可行的,那就是,直陈条件句有真假值和亚当斯论题是相容的。这样的立场看起来似乎很接近杰克森对亚当斯论题的解读([13]),但杰克森并不认为他的理论可以解决贫乏性结果([14])。3这主要的原因是杰克森无法提出一个令人满意的一般性理论,如耶皮亚(Anthony Appiah)指出,一旦杰克森的理论跨足到简单条件句之外,其理论便会有不好的结果([3])。本文捍卫的立场是来自于[28]为亚当斯论题提出的看法,本文会在第2节介绍该文对于直陈条件句提出的三值语意论,说明他如何去解读亚当斯论题,并在最后论证他的理论如何能避免贫乏性结果。
为便于讨论,我们有必要先厘清牵涉到直陈条件句的语句之结构,基本上,笔者依其复杂度区分以下几种不同的语句:
简单直陈条件句(simple indicative conditionals)A→B里的A或B不能再是直陈条件句,也不能是由直陈条件句所组成的语句。
嵌套直陈条件句(nested indicative conditionals)A→B里的A或B是直陈条件句,例如,(A→(B→C)),((A→B)→C)。
直陈条件句的复合句(compounds of indicative conditionals) 直陈条件句和其它语句组成的连言句或选言句,例如,(A∧(B→C)),(A∨(B→C))。
对一个主张直陈条件句有真假值的理论而言,不能去限制直陈条件句可以和∧,∨,→等逻辑连接词形成新的语句,因此,其理论应该要能适用于以上三种不同的语句,否则其理论就缺乏一般性。由于亚当斯并不主张直陈条件句有真假值,因此他认为亚当斯论题只适用于简单直陈条件句,他这样的想法后来得到爱君腾(Dorothy Edgington),贝内特(Jonathan Bennett)等人的支持([5,7])。4本文主要的焦点在于有真假值的直陈条件句理论、亚当斯论题、和贫乏性结果如何共存,因而无法进一步讨论直陈条件句没有真假值的看法。
为利于表述,本文以下便直接用条件句来表示直陈条件句。[28]同样认为亚当斯论题只适用于简单条件句,然而,该文只说明了他的理论如何避免刘易士的第一个贫乏性结果,关于其它的贫乏性结果,他仅提供一条原则上可行的进路去解决。另外,哈耶克认为就算亚当斯论题只限用于简单条件句,仍然会受到贫乏性结果的挑战([11])。关于此点,[28]并没有做出正面的响应。笔者要论证该文提供的进路的确是可行的,本文会在第二节介绍刘易士前三个贫乏性结果([19,20]),然后在第三节介绍刘易士的第四个贫乏性结果([20]),和哈耶克的一个很重要的贫乏性结果([9])。接着在第四节,笔者会明确地指出贫乏性结果的根源。然后在第五节说明[28]的理论如何解决所有的贫乏性结果,并试着响应哈耶克提出的挑战。作为结论,本文认为[28]对亚当斯论题提出的解读,可以避免市面上所有的贫乏性结果。
2 一种对亚当斯论题的解读
本节要介绍[28]对条件句发展出来的理论,该文基于麦克德莫特(Michael McDermott)的一些想法([22]),提出以下一个一般性的三值条件句真值表,以表1呈现如下:

表1:三值条件句真值表
表1中的T、F、X分别代表了真、假、没有真假,它和麦克德莫特提出的看法有几点重要的不同:第一,对于¬,∧,∨的定义采取了乌卡西威契(Jan Łukasiewicz)的三值逻辑系统([21])以及克林(Stephen Cole Kleene)的强三值语意论([17]);第二,引入了∽来定义“没有真假”,例如,∽S的意思是“语句S没有真假”。基于表1,有以下的定义及公理:([28],第39–41页)
定义1.P(A→B)=P(AB)。5P(AB)代表P(A∧B),这是文献上的惯例,本文以下也以依惯例,把P(A∧B∧,...)省略为P(AB,...)。
定义2.P(¬(A→B))=P(A¬B)。
定义3.P(∽(A→B))=P(¬A∨∽A∨∽B)。
公理1.对任何语句A,0≤P(A)≤1。
公理2.如果A和B是等值的,P(A)=P(B);P(¬A)=P(¬B);P(∽A)=P(∽B)。
公理3.如果A和B是不兼容的,P(A∨B)=P(A)+P(B)。
公理4.P(S)=1,S是样本空间。
由以上的定义和公理,可以证明P(A→B)+P(¬(A→B))+P(∽(A→B))=1([28],第41页)。因此,概率值对条件句的分配,不会有不一致的情况产生。
将概率应用到没有真假的语句上乍看之下有点奇怪,然而,让我们从打赌条件句A→B来思考这个问题。当你非常确认A为假时,你应会认为此时打赌A→B没有输赢,你似乎可以认为打赌A→B赢的概率为0;打赌A→B输的概率也为0。在这样的想法下,一个没有真假的语句为真的(或为假的)概率为0似乎不是太奇怪的主张。从另一个角度来说,我们可以把没有真假理解成不是为真的情况,也不是为假的情况,[28]的机率理论是应用到这三种互斥且穷尽的情况。既然X没有真假,代表着它不是为真的情况,所以为真的概率为0。它也不是为假的情况,所以为假的概率为0。
一旦确认了三值条件句的概率分配不会有不一致的情况,[28]接着用公平赌率的概念来定义可断说性,借用杰弗里的例子([16]),设想打赌A→B被设计成彩票一的形式,如图1:

图1:彩票一
而彩票一的价值会是另外两张彩票(彩票二及彩票三)的价值总合,如图2:

图2:彩票二、彩票三
现在,假设你对彩票一愿意押的最高赌注是x元,我们只要知道在这样的假设下,彩票二和彩票三的价值总和是多少,就可以知道x的值。我们可以看到,彩票二值P(AB)元,而彩票三值P(¬A)×x元,所以,彩票一的价值x等于彩票二的价值P(AB)加上彩票三的价值P(¬A)×x。因此,x=P(B|A),而P(B|A)代表了,打赌者打赌条件句愿意下的最大赌注x除于可获得的奖金1,而这正代表了打赌A→B的公平赌率。6事实上,这样的想法最早可追溯到德费内提([8],第68–69页)。
以上的打赌方式只适用于简单条件句,一旦A→B的前件没有真假时,就无法衡量它的价值,因此,[28]中进一步地把这样的思维扩展到所有的条件句。由于[28]已经给出更复杂的条件句之概率定义,就可以计算这些语句为真、为假和没有真假的概率值,就可以去评价有牵涉到条件句的语句之公平赌率,也就可以进一步去定义它的可断说性。为了和杰克森的可断言性做区分,笔者用Assa(S)来代表S的可断说性,那么,根据[28]对可断说性的定义,Assa(S)会等于打赌S的最大赌注除以打赌S赢的奖金。
现在,假设S代表了一个条件句C→D(C,D本身也有可能是条件句),打赌C→D赢的奖金为n元,而一个理性的人打赌C→D愿意下的最大赌注是x元,那么,我们会面对如图3的彩票:

图3:彩票一∗
这使得我们对彩票一∗的最大赌注x=n×P(CD)+x×P(¬C∨∽C∨∽D)。因此,x/n=P(CD)/[P(CD)+P(C¬D)]=Assa(C→D)。7

也就是说,对于所有的条件句而言,有以下的定理:([28],第42页)
定理1.Assa(A→B)=P(AB)/[P(AB)+P(A¬B)]。
定理1是条件句的可断说性最一般的定义,当A→B是简单条件句时,也就是A与B都是真值函数的二值句式时,P(AB)+P(A¬B)=P(A)。因此,当A→B是简单条件句时,A→B的可断说性等于P(B|A),换句话说,我们可以把亚当斯论题视为是定理1的特殊情况。
总言之,基于三值语意学下和对简单条件句的打赌方式,[28]对亚当斯论题的解读是:

在A→B是简单条件句的条件下,条件概率等于打赌A→B的公平赌率,这说明了为何人们在评价简单条件句时,会根据条件概率来判断。然而,贫乏性结果揭示了条件概率不代表是简单条件句“为真的概率”,因此,[28]建议我们最好把它视为是简单条件句的“可断说性”。我们可以看到,[28]区分了条件句为真的概率和可断说性,但这为何能避免贫乏性结果呢?笔者接下来说明几个重要的贫乏性结果和其根源,并在最后替[28]阐明可断说性的意义,以解决贫乏性结果。
3 刘易士的前三个贫乏性结果
在本节中,笔者将介绍三个刘易士的贫乏性结果,并说明[28]如何解决刘易士的第一个贫乏性结果([19])。这三个贫乏性结果都依赖于刘易士所谓的条件化函数是用来捕捉条件概率的意义,当P(φ)>0时,一定有一个概率函数使得只要我们承认有这样的函数,加上(SH),一定可以得到:8这里有个条件:P(A∧B)>0。

而主张条件句是个二值命题的人且接受经典概率理论的人,在P(AC)>0的条件下,也一定会同意以下的等式:

现在,如果→是刘易士所谓的“普遍概率条件句”(universal probability conditional),即,对任何命题A,C,只要P(A)>0,(SH)都会成立,也就是说,P(A→C)=P(C|A)。而依照(1),P((A→C)|C)=P(C|(A∧C))=1,P((A→C)|¬C)=P(C|(A∧¬C))=0,代入(2)后,即可得到

(3)这个结果是令人无法接受的,因为它告诉我们的是,在P(AC)和P(A¬C)都大于0时,假如我们还坚持(SH),C和A会是概率上独立的。此时,要避免(3)的唯一可能是,有普遍概率条件句的语言之表达力非常弱,弱到无法同时表达三个都有可能,而且彼此互不兼容的语句。刘易士称这样的语言为“贫乏的”(trivial)。因此,刘易士的第一个贫乏性结果是:
任何一个有普遍的概率条件句的语言,是一个贫乏的语言。([19],第300页)
可是,我们使用的语言不是贫乏的,所以,(SH)在我们使用的语言里是无法成立的。刘易士接着设想,也许有人会觉得第一个贫乏性结果是我们把→解释成普遍的概率条件句所致,那么,只要我们不要把→做此解释,而把它解释成特定的概率函数集合之概率条件句就可以避免贫乏性结果。比如,既然我们关心的是主观概率,即,那些用来代表我们信念系统的概率函数,那么,我们可以把P这样的概率函数对某个语句给出的值,解释成某人在某时间点上对某个语句的主观概率。换句话说,我们可以把P视为一种信念函数,用来代表我们的信念系统,而把→解释成我们信念函数集合的概率条件句即可。
刘易士的第二个贫乏性结果便基于这样的想法,他现在只考虑能代表我们信念系统的概率函数,假设P是我们信念函数的集合,而且是条件化下封闭的。例如,P是某甲对A,B,C……等的信念函数,我们可以由P条件化任何语句,例如,A。当甲的P在得知A这个证据后,他的信念函数会变成他对其它语句的主观概率变成而且仍会是一个恰当的信念函数。如果我们把→解释成P的概率条件句,由于P里面的概率函数P同样地都会遵守(SH)和标准概率定律,一样会导致同样的结果,而得到(3)这个式子。这样的后果是:为了要避免(3)这个结果,P对每一个语句最多只能给出四个不同的值。为什么呢?对任何的语句F和G而言,我们可以用表2来表示其概率分配。其中,I至IV分别表示四个割集合,它们互斥且穷尽了所有的可能性。

表2:概率分配
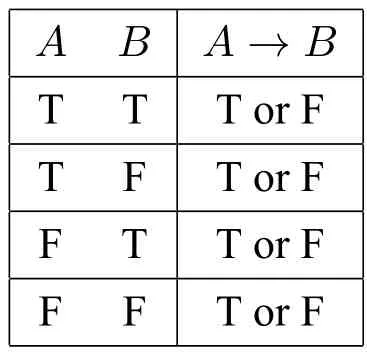
根据表2,P(F)=I+III,P(G)=I+II,P(¬F)=II+IV,P(¬G)=III+IV。刘易士的第一个贫乏性结果已证明:若P(FG),P(¬FG),P(F¬G)和P(¬F¬G)其中有三个大于0,由于它们彼此不兼容,那么,一定会出现结果(3)。为了能够避免(3),只有两种可能:(i)其中一个割集合的概率为1:那么其它三个割集合的概率均为0。(ii)没有任何一个割集合的概率为1:如果其中一个割集合的概率为x(0 这样的结果导致P对语句最多只能给出四个值:1,0,x和1−x,才不会产生结果(3)。但刘易士称这样的P为贫乏的,因为能代表我们信念系统的概率函数,不应对每个语句最多只能给出四个不同的值。所以,刘易士证明了第二个贫乏性结果: 如果一个概率函数的集合是条件化下封闭的,除非此集合全然由贫乏的概率函数所组成,否则不会有此集合下的概率条件句。([19],第302页) 既然有些代表我们的信念系统的概率函数不是贫乏的,也就是说,我们对语句的主观概率可以超出4个不同的值,我们所使用的条件句并不是一个符合史东内克假说的概率条件句。 在刘易士的第一个和第二个贫乏性结果之后,其他的人才意识到史东内克假说竟会产生令人如此惊讶的结果,支持史东内克假说的人试着质疑刘易士论证里的预设,冀望能避免刘易士的贫乏性结果。于是,刘易士针对他会遭遇的两个反对,再提出两个贫乏性结果。([20])刘易士遭遇的第一个反对是,不是所有的命题都可以视为证据,即使认为信念函数P条件化某人的全部证据(total evidence)之命题而来的函数能做为信念函数,不代表信念函数的集合会一般地条件化下封闭的。第二个反对是这样的函数不应该被视为我们的信念函数。 笔者先说明刘易士针对第一个反对所给的第三个贫乏性结果,在刘易士的第二个贫乏性结果里,他假设能代表我们的信念函数集合是一般地在条件化下封闭的,也就是说,所有的都属于信念函数的集合,不过,他承认我们没有好的理由来做这样的一般性预设。因此,反对者会说,假设P是某人甲原本对A,B,C,...的信念函数,当甲知道A为真时,他对其它命题的主观概率变成只要A能够是甲的证据命题,便可以是甲的信念函数之一。换句话说,不是条件化所有的命题φ后所形成的都可以代表信念函数,要能做为证据命题的φ才可以。也因此,φ必须是一个确切的命题,然而,刘易士在论证里用来条件化的命题是C和¬C。反对者认为即使C是一个确切的命题,¬C却不是,两者不能全部都是证据命题,所以,之中只有一个才可以是信念函数,刘易士的第二个贫乏性结果里使用的并不是一个恰当的信念函数。 刘易士完全同意这是一个合理的反对,他应该只预设条件化证据命题下封闭的信念集合,于是他修改原本的预设:考虑一个证据命题集合Σ,它代表甲在特定的时间点上可获得的全部证据(total evidence available)。C,D,...是Σ里的命题,而且它们是互斥的且穷尽整个证据命题集合。由于一个人的区辨能力是有限制的,这样的命题会是有限的,但至少有两个以上,因此它们是一个有限的分割集合(finite partition)。现在,假设P是甲信念函数的集合,而且是在条件化C,D,...下封闭的,令P是P其中的一个信念函数,且P(C),P(D),...均大于0。另外,令A是会使得P(A|C),P(A|D),...都大于0,且P(C|A)̸=P(C)的命题,若没有这样的P,C,D,...和A,则刘易士称之为贫乏的。 据此,我们可以得到: 然而,一旦我们认为对P里的信念函数而言,史东内克假说都会成立,刘易士用(*)来代表史东内克假说:([20],第581页) 由于P((C∧A)|C)=P(CAC)/P(C)=P(CA)/P(C)=P(A|C),所以等式右边的第一项P((C∧A)|C)P(C)÷P(A|C)就等于P(A|C)P(C)÷P(A|C),也就等于P(C);而由于C,D,...是不兼容的,所以P((C∧A)|D)和其之后的P((C∧A)|−)都为0,也就是说,原式最后为: 可是,在一开始的假设里,P(C|A)̸=P(C),因此,史东内克假说不可能对P里的信念函数都成立。刘易士让我们看到,即便我们限制可用来做为条件化的命题,还是无法避免会导致第三个贫乏性结果: 对于条件化某个分割集合中的命题是封闭的概率函数集合而言,除了在贫乏的案例下,没有一个一致的方式来解释→,使得(*)对整个集合都成立。([19],第583页) 因此,光是限制可做为条件化的命题,不足以阻挡刘易士的贫乏性结果。 我们可以看到,刘易士的前三个贫乏性结果的论证策略是:(SH)加上条件化函数和标准概率会导出(3)。由于[28]对条件句的概率理论不支持(SH),所以,他解决第一个贫乏性结果的方式是去否认(SH)来阻断(3)的产生。在[28]的理论下,(1)不会成立,因为P((A→C)|B)=P((A→C)∧B)/P(B)=P(ABC)/P(B)。所以,无法如同刘易士那般藉由(1)而导出(3)。[28]中这样的方式同样可以解决第二个贫乏性结果。 但是,[28]的策略是否可以解决第三个贫乏性结果则有待考虑,因为,第三个贫乏性结果并没有导出(1),也可以导出(3)。敏锐的读者也许会发现,[28]对前两个贫乏性结果的解决方案令人留下一个疑虑,那就是,该理论会不会有不从(SH)而导出(3)或类似结果的途径?换句话说,(SH)并不是贫乏性结果的必要条件,我们需要找出一个贫乏性结果共有的病因,才能对症下药解决贫乏性结果。该文中虽然有意识到这个问题,并试图从爱君腾对贫乏性结果的诊断提出一个原则性的解决方式,但并没有详细说明那的确是可行的进路。因此,本文接着要介绍其它的贫乏性结果,进一步详尽地刻画并扩展[28]提出的原则性方法,说明这个原则性的进路如何可行。 在讨论完第三个贫乏性结果之后,刘易士认为他还会遭遇第另一个反对,这样的函数不应该被视为我们的信念函数。刘易士的前三个贫乏性结果中,有一个很关键的角色是由所扮演,这样的函数涉及到信念的变动,我们可以用以下的说明来理解: 假设P是某人的信念函数,他对A,C,A∧C的主观概率分别为P(A),P(C),P(CA)。当他对A的主观概率变为1时,这个人对其它命题的主观概率有可能会因此而有所不同,此时,我们可以说他的信念函数由P变成 问题是,我们对某命题的主观概率提升时,它很少变成1,也许它提升至0.8或0.9,那么变动过后的信念函数就不会是换句话说,刘易士的只是一个极端的特例,它只能捕捉到信念变动里一个很极端的情况,有些人认为一个理性的人变动过后的信念函数不应该是这样的极端,所以不应该做为一个恰当的信念函数。那么,什么才是一个恰当的信念函数呢? 杰弗里(Richard Jeffrey)对这个问题提出令人信服的看法([15],第166–171页),他要我们考虑以下的例子: 有一匹赛马在泥泞的场地上表现得特别出色。如果一个晴朗的气象预报使得一个赌徒改变他对命题B“场地会是泥泞的”的信念程度,那么,他对命题A“那匹马将赢得一场特定的赛事”的信念程度应该会改变。然而,那个预报应该对他对“在场地是泥泞的条件下,那匹马将会赢”这个命题,或者“在场地不是泥泞的条件下,那匹马将会赢”这个命题的信念程度,不具任何影响。([15],第169页) 一个赌徒对A的主观概率P(A)会随着对B的主观概率P(B)的变动而改变,以上面的例子来说,此赌徒对B信念的提升会使得他对A的信念提升。为了和刘易士的P′φ做区分,笔者用Pφ表示杰弗里的条件化函数。而杰弗里认为,不管PB(B)如何变动,PB(A|B)和PB(A|¬B)应该都会是保持不变的。所以: 让我们假设赌徒甲相信“赛马H在泥泞的场地条件下赢得比赛”的概率是0.8,即P(A|B)=0.8;而且甲相信“赛马H在正常的场地条件下赢得比赛”的概率是0.1,即P(A|¬B)=0.1。明天就要比赛了,本来他的P(B)是相当低的(只有0.3),导致他的P(A)也是不高的,只有0.31。9P(A)=P(AB)+P(A¬B)=P(A|B)P(B)+P(A|¬B)P(¬B)=0.8×0.3+0.1×0.7=0.31。然而最新的气象报告显示明天很有可能会下雨,也就是说,明天比赛的场地很有可能是泥泞的,于是此时他对B的主观概率,也就是PB(B),增加为0.6。那么,他如今对此匹赛马在泥泞的场地中赢得比赛的主观概率,也就是PB(A|B),应该是保持和原先一样的。根据条件概率的定义: 我们又知道: 由(a)和(b),我们便可以得到:10杰弗里原文并不是用“(GC*)”这个名称,笔者为了方便讨论而称之为“(GC*)”([15],第169页) 我们可以称杰弗里的(GC*)为“一般条件化”(Generalized Conditionalization),可以用来计算在一般的情形下,我们对某命题的主观概率改变后,其它的命题会如何改变。 现在,我们可以将上面赛马之例子带进(GC*),便可以得到在明天场地会变泥泞的主观概率提升后,对赛马H赢得比赛的主观概率应为: 这和(GC*)只是写法不同,而意思是一样的,不过,要特别注意的是,等式两方的x之意义是不一样的,请容许笔者稍做说明。 (GC)左边的Px代表由P一般条件化某个命题φ而来的函数,即PC。(GC)右边的x代表甲对命题φ的主观概率改变后相差的数值。例如,甲原本的P(C)是0.3,后来变成PC(C)为0.8,那么x=0.8−0.3=0.5,换句话说,x=PC(C)−P(C)。经过这样的说明后,按照(GC): 把右边展开后便得到(GC*)。11请参阅附录中的1。 让我们开始来看看刘易士如何得到第四个贫乏性结果,假设有某个信念函数P和证据命题C,P(C)和P(¬C)都大于0。令有个命题A会使得P(A|C)和P(A|¬C)都大于0,而且P(A|C)不等于P(A|¬C)。如果无法给出这样的P,C和A,刘易士便称之为贫乏的,而我们的信念函数可以给出这样的例子。现在,假设对所有的信念函数而言: 依(GC)可得到:12请参阅附录中的2。 最后会得到:13请参阅附录中的3。 以上的等式只有在左右两边都等于0才会成立,因为当我们给定P,A和C时,此时会变动的只有x,如果无论x怎么变动,等式都会成立的话,唯一的可能是左边的式子等于0。有两个情况会使得左式等于0,第一种可能是P(A|C)=P(A|¬C),但这违反一开始的预设;第二种可能是P(A→C|C)=P(A→C|¬C),这表示: 在刘易士的预设里,P(A|C),P(¬C|A),P(C|A)和P(A|¬C)都会大于0,所以上述的等式不会成立。因此,刘易士证明了第四个贫乏性结果:([20],第588页) 对信念变动符合(GC)下会封闭的信念集合而言,除了在贫乏的案例下,没有一个一致的方式来解释→,使得(*)对整个集合都成立。 刘易士的四个贫乏性结果是条件句理论里非常重要而影响深远的论证,除非支持史东内克假说的人能提出更令人信服的条件化函数,并证明不会有类似刘易士的贫乏性结果,否则便得论证说我们对条件句的主观概率不涉及到信念的变动。哈耶克进一步论证,其它的条件化函数也无法避免贫乏性结果([11]),其他人则论证即使条件句的主观概率不涉及信念的变动,仍然会使得史东内克假说无法成立([6,9,10,27])。而在这些贫乏性结果中,哈耶克提出的壁花论证(Walflower argument)所用的前提最弱,使得它成为最强而有力的贫乏性结果([9]),笔者接下来便要说明这个论证。 哈耶克给了一个简明的例子来说明壁花论证:([11],第156页) 考虑公平的三张彩票,以及由三个语句“彩票i赢”,i=1,2,3所产生的布尔代数(Boolean algebra)。令P被定义是作用在这个代数上的自然函数,它对这三个语句的每一个都分配概率值1/3。这样的后果是每一个布尔代数的成员都有一个1/3倍数的概率值。然而,很多条件概率不是1/3的倍数,例如,P(彩票1赢|彩票1赢或彩票2赢)=1/2。所以,有条件概率在非条件概率中找不到匹配。 哈耶克戏称条件概率和非条件概率就像是两群去参加舞会的男女,条件概率的数量代表男生的数量,非条件概率的数量代表女生的数量,而男生总是会多于女生,因此,总是有些男生会找不到对应的舞伴而必须当壁花,故称之为“壁花论证”。([11],第 157 页) 在哈耶克的论证中,他没有对→做特别的解释,只接受→是一个二位连接词,当A和C代表两个不同的命题时,A→C也会是一个命题。P代表一个人的主观概率函数,如果一个人能区分不同的可能世界,P就会分配给这些可能世界一个特定的值,而哈耶克预设一个人能区分的可能世界是有限的。假设某人能区分的可能世界有n个,而它对这些可能世界之主观概率分别为:P1,P2,...Pn。而如下图4所示: 图4:非条件概率 哈耶克称P1,P2,...Pn为“非条件概率”(unconditional probabilities),而既然命题为真的概率等于其为真的可能世界之概率总和,在这样的设定下,任何命题为真的概率要么等于这些非条件概率之一,要么等于它们其中几个的总和。 哈耶克原本的论证颇为复杂,为了简单说明,笔者模仿他后来给的彩票例子,令P1=P2=,...=Pn=1/n,而Ai代表“彩票i会中奖”。这样一来,所有命题为真的概率会是1/n的倍数,而且命题为真的概率一定会等于某个相对应的条件概率所给出的值,只要令给定的条件为恒真句即可(例如,P1(_)对应到的是P1(_|T))。然而,有些条件概率的值却不是1/n的倍数,例如,在哈耶克给的3张彩票例子中,n=3,而P(彩票1赢|彩票1赢或彩票2赢)=1/2,1/2并不是1/3的倍数。简言之,在以上的假定下,假如我们把A→C当成一个命题,它的概率值一定是非条件概率函数的倍数。而(SH)说在P(A>0)的条件下,P(A→C)一定会等于P(C|A),那么P(C|A)必须是非条件概率函数的倍数。遗憾的是,哈耶克的壁花论证告诉我们,P(C|A)未必是非条件概率的倍数;因此(SH)会导致不一致的结果。这个论证没有用到两个不同的主观概率函数来看待同一个条件句,而且不默认任何条件句逻辑,只要求当A和C代表两个不同的命题时,A→C也会是一个命题,但(SH)在这么弱的前提下依旧无法成立。 哈耶克认为壁花论证不仅驳斥了(SH),还可以驳斥亚当斯论题的任何解读([11])。他说: 为了和条件概率一样多,可断言性可以多过概率是够令人惊讶的。我的疑惑被加倍地增大,更加疑感的是,条件句的可断言性可以和概率一样多是令人惊讶的,更令人惊讶的是,简单条件句的可断言性可以一样多。([11],第158页) 不尽是可断言性,哈耶克认为不管是可断说性,或是可接受度都是令人怀疑的([11],第159页)。因此,他不认为亚当斯论题是条件句理论中的试金石(touchstone),更不认为条件概率在条件句中扮演重要的角色。不过,关于这个对亚当斯论题的攻击,哈耶克自己承认说:“我了解到这不是一个决定性的论证”([11],第158页)。哈耶克要的是支持亚当斯论题的人能为它提供一个合理的基础,而不只是去诉诸直觉,可惜的是,[28]中没有为此点提供更实质的说明,笔者会在第五节针对此点做出回应。 以上这些各式各样的贫乏性结果是令人眼花瞭乱的,大多数人在一开始接触亚当斯论题时,都会觉得这是可信的主张,然而贫乏性结果动摇了大家对亚当斯论题的信心。即使我们去反对一开始提出贫乏性结果的刘易士所承认的前提,我们仍然难以反驳后继者运用更弱的前提来导出类以的结果,这是很令人沮丧的。这样的现象反映出了什么?会不会条件句真如同亚当斯所说,并没有所谓的真假值呢?因此,当我们试图应用“真”和“假”的概念到条件句时,无可避免地便会有这样令难堪的情形产生呢?笔者不认为如此,下一节,笔者要来说明本文支持的AT如何避免这些贫乏性结果。 为何(SH)会有贫乏性结果呢?我们可以从卡尔斯壮(Ian F.Carlstrom)和希尔(Christopher S.Hill)提出的贫乏性结果中看出端倪。([6])卡尔斯壮和希尔先默认对任意且逻辑上独立的句子A和B,我们可以分配真假值给句子A→B,且令P(A→B)=P(AB)/P(A)。那么,A→B的真值表可能如表3: 表3:A→B的真值表 假如A→B是由A和B所建构出来的布尔式语句(Boolean sentences),则有16种可能的真值分配方式。但在这样的假设下,A→B的真假值不可能光凭A和B的真假值来决定,因为不存在一个A和B建造出的布尔式语句X,使得所有的概率函数P让P(X)=P(AB)/P(A)。 笔者先来证明其中一个例子,假设X代表了A→B的真值条件(无论它是什么),且其真值分配为⟨F,F,T,F⟩,也就是表3中A→B第一列到第四列的值。现在,考虑如图5的四个可能世界,以及概率分配方式: 图5:可能世界以及概率分配方式 在这样的设定下,P1(AB)=0.2,P1(A)=0.4,P1(X)=0.5,因此P1(X)=P1(AB)/P1(A)。然而,另一个概率函数P2对这四个世界的概率分配值未必和P1一样,我们可以看到,P2(X)便不会等于P2(AB)/P2(A)。也就是说,在这样的真值分配下,一定有些概率函数Pi使得Pi(X)̸=Pi(B|A),因此Pi(A→B)̸=Pi(B|A)。同样地,在其它另外的真值分配下,也会有同样的情况产生,因此A→B不是由A和B所建构出来的布尔式语句。 既然A→B不是由A和B建构成的布尔式语句,当我们知道A和B的真假值时,也无法决定A→B的真假值。因此,支持A→B是二值语句的人,只能假定A→B在每一个可能世界中非真即假,而且无论如何,P(A→B)=P(B|A)。不过,卡尔斯壮和希尔接着给出一个贫乏性结果来反驳以上的想法。([6])由于他们的例子比较不易了解,笔者介绍爱君腾的另一个版本的贫乏性结果来说明。([7]) 令A→B所代表的命题为X,考虑如图5四个可能世界,以及两种概率分配方式P2,P2:14爱君腾给的是一个最无争议的例子,因为A→B在A和B都为真时为真,在A为真B为假时为假是比较合理的。然后,在A为假时,我们无法确定A→B的真假,所以它在有些¬A的世界中为真,在有些¬A的世界中为假。 图6:可能世界以及概率分配方式 因此,爱君腾对贫乏性结果的诊断如下:([7],第274页) (i)P(B|A)取决于A的世界(A为真的割集合部分)之概率如何分配,固定了P(A)和P(BA),也就固定了P(B|A)。 (ii)任何满足P(X)=P(B|A)的命题X,会在有些而不是全部的¬A世界中为真,所以P(X)不只取决于A世界的概率如何分配,还取决于¬A世界的概率如何分配。 (iii)有不同的概率分配方式,它们会同意A世界的所有分配值,但不同意¬A世界的分配值。它们会同意P(A)和P(BA)是一样的,因此,会同意P(B|A)是一样的。而且,它们同意P(AX)是一样的,但它们不同意P(¬AX)会是一样的。由于P(X)=P(AX)+P(¬AX),它们不同意P(X)会是一样的。所以,有一些概率分配方式会使得P(X)̸=P(B|A)。 简言之,贫乏性结果来自于有两种计算P(A→B)的方式,两者却会有相左的结果。第一种是把它等同于P(B|A),即(SH)。第二种笔者称之为概率总和论题,表述如下: 概率总和论题对任何条件句A→B,P(A→B)等于A→B为真的可能世界之概率总和。 而贫乏性结果所显示的是,我们总是可以找到一种概率分配方式,使得(SH)和概率总和论题会有不一致的情况产生。 我们可以在本文介绍的贫乏性结果里都找得到这样的特征,像刘易士的前两个贫乏性结果都依赖于前提(2): 这也是意味着,A→C为真的概率等于A→C且C为真的世界之概率总和,加上A→C且¬C为真的世界概率总和,也就等于A→C在它为真的世界之概率总和,但这不总是等于P(C|A)。刘易士的第三个贫乏性结果是把{C,¬C}换成{C,D,...},但意思是一样的。至于刘易士的第四个贫乏性结果,是把A→B应用到杰弗里的一般条件化函数,使得 这背后的想法如贝内特所言: 如果PB(A)=0.5,对于C的新概率值会从A那里获得一些推升……但这不是全貌。……我们的理想思考者指派一些新的正概率值给¬A(因为他对A的新概率值小于1);如果在给定¬A下,他也指派正概率值给C,他对C的全部新概率值也从这里得到推升……所以我们把这次的推升和之前的加在一起。这就是(GC)说我们应该做的。([5],第66页) 把以上引言中的A当成C,C当成A→C,刘易士的第四个贫乏性结果是去计算C的概率值有变化时,A→C的概率值应该如何变化。首先去计算(A→C)∧C与(A→C)∧¬C概率值之变化,再把两者加总起来。同样地,PC(A→C)不总是等于PC(C|A)。哈耶克的壁花论证也是去加总A→C在它为真的世界之概率值,也同样地不总是等于P(C|A)。 因此,要避免贫乏性结果,首先,必须去确保自己的条件句概率理论和概率总和论题会有相同的结果。另外,如果我们把爱君腾的诊断中之概率换成可断说性,也就是,把P(A→B)换成Assa(A→B),而且又主张可断说性总和论题—Assa(A→B)等于A→B可断说的世界之可断说性总和。同样地,就一定找得到两种计算Assa(A→B)的方式,而且两者不相等,一样会有贫乏性结果。下一节,笔者将论证[28]的理论如何避免贫乏性结果。 论文[28]中的理论虽然区分了条件句为真的概率与可断说性,但光是做出这样的区分还不足以避免贫乏性结果。正如刘易士所说:“并不是真和概率之间的关联导致我的贫乏性结果,而只是应用标准概率到条件句的概率造成的”([19],第304页)。有鉴于此,亚当斯的所采取的方式是:“我们应该把概率不适用于条件句的复合语句当成概率的基本限制,这和真不适用于简单条件句是同等的”([2],第35页)。要注意的是,刘易士和亚当斯在这里会说条件句的“概率”,主要是针对当初亚当斯在表述亚当斯论题时,并没有去区分为真的概率与可断说性,而只是用“概率”一词来表示,他们实际上谈的是“可断说性”。换句话说,刘易士的主旨是要说,Assa这样的函数一定要有某些规则来规范,假如Assa所依循的规则和标准概率函数P没有两样,贫乏性结果还是会如影随行。 对此,亚当斯的策略是去限制Assa只适用于简单条件句,使得简单条件句以外的条件句在他的理论里是无法被讨论的。因此,对所有简单条件句A→B,和任一语句C,Assa(A→B)不能是Assa((A→B)∧C)和Assa((A→B)∧¬C)的总合,因为后面两者都是没有定义的。换句话说,亚当斯会否认可断说性总和论题,如此一来,对简单条件句A→B来说,Assa(A→B)只有一种计算方式——P(B|A),贫乏性结果便无所施力。 然而,哈耶克对于亚当斯的策略提出一个质疑。哈耶克的壁花论证显示,条件概率函数的数量一定会多于非条件概率函数的数量,即使我们只谈论简单条件句。哈耶克认为概率函数已经足以去涵盖所有的功能,他怀疑Assa如何能做到概率函数无法做到的事,去指引我们如何去打赌条件句,他质疑这如何可能?他要主张(AT)的人替Assa给出一个好的说明。因此,还要解决三个问题:第一,由于[28]承认有条件句为真的概率,得确保在其概率理论下,条件句的概率计算会和概率总和论题有相同的结果。第二,[28]的可断说性理论在简单条件句时,可以像亚当斯那样否认可断说性总和论题,但他得说明Assa的角色来响应哈耶克的质疑,说明我们为何需要概率函数之外的可断说性函数。第三,[28]的可断说性理论还可以应用到到简单条件句以外,如何证明那不会有贫乏性结果? 在[28]对条件句的概率理论下,P(A→C)会等于P(AC)。由于[28]是把经典概率扩充到可以处理三值语句,让概率空间多了“没有真假”的情况,那么,对A→C和C这两个语句来说,我们都得考虑A→C分别在C为真的世界(C),C为假的世界(¬C),C没有真假的世界(∽C)中的概率值。因此,依照概率总和论题,[28]应该要有类似刘易士的(2)的等式: 若(2**)最后的结果不等于P(AC),则[28]的条件句概率理论就会有贫乏性结果。幸好,对该理论而言,会有以下的结果: 因此,[28]的理论不像刘易士的结果(3)那样,使得条件句的概率和概率总和论题有不同的结果。不过,我们还是会质疑说,这很有可能是由于C是A→C的后件,才会得到(3**)这个结果,假如把C换成其它语句,(3**)就有可能不会成立。 现在,对任何条件句A→C和语句B而言,我们会有以下的式子: 接着,我们可以得到: (†:根据定理([28],第41页):P(A)=P(AB)+P(A¬B)+P(A∽B))所以,[28]可以解决第一个问题,该理论中条件句之概率计算会和概率总和论题有相同的结果。 接着,让我们来检视[28]对可断说性的计算方式。其中,对于可断说的想法源自于麦克德莫特([22]): 这样的结果之一是,Assa在对任何二值语句分配可断说值时,会和概率函数给出相同的值。因为对任何二值语句φ而言,P(φ有真假值)=1,所以, 接着,当Assa所面对的是简单条件句φ→ψ时,Assa会去条件化φ→ψ有真假值的情况,也就是去条件化φ,因此 至于其它更复杂的语句之可断说性,有以下的定理([28],第43–45页): 定理2.Assa(A→(B→C))=P(ABC)/[P(ABC)+P(AB¬C)]。 定理3.Assa((A→B)∧C)=P(ABC)/[P(ABC)+P((A∧¬B)∨¬C)]。 定理4.Assa((A→B)∨C)=P((A∧B)∨C)/[P((A∧B)∨C)+P(A¬B¬C)]。 我们可以看到,定理2–4涵盖了非条件句和简单条件句以外的语句。 至于一个否定句,我们可以很简单地依据定义而得到以下的定理: 定理 5.Assa(¬φ)=1−Assa(φ)。 所以,对于条件句和其它逻辑运算符形式的复合语句,都有明确的计算方式,并且被概率值所决定。当语句的概率值都有唯一的结果时,可断说值也会是唯一的,换句话说,在[28]的理论下,只要语句的概率值没有贫乏性结果,它的可断说值也就不会有贫乏性结果。所以,第三个问题也可以得到[28]的理论回应。 然而,[28]没有说清楚他使用的概率函数和可断说性函数之间有一个重要而根本的差异,而笔者认为这个差异可以让我们以另一个角度来诊断贫乏性结果的根源。以哈耶克用的术语来说,[28]所使用的概率函数是一种非条件概率函数,而他使用的可断说性函数是一种条件概率函数,笔者建议我们用一元概率函数和二元概率函数来做区分。一元概率函数是对单独的一个语句分配概率值,二元概率函数则是对两个语句的序对分配概率值。史东内克([26])当初在论证(SH)时便使用这两种不同的概率函数,他试图论证一元概率函数对条件句A→B所分配的概率值,会等于二元概率函数对(B,A)所分配的概率值,15关于此点,[28](第7–9页)曾做过详尽的讨论。正是这个错误的想法产生了贫乏性结果。 刘易士论证的是,一元概率函数对φ→ψ所分配的概率值,并不总是等于二元概率函数对(ψ,φ)所分配的概率值。哈耶克的壁花论证则进一步告诉我们这背后的理由是,二元概率函数所能分配的概率值,会远远多于一元概率函数能分配的概率值。所以,每当二元概率函数对语句序对(B,A)分配概率值x时,我们就可以建构出A→B这个条件句;但很有可能无法回头找到一个一元概率函数,使得它会对A→B给出同样的x值。哈耶克要我们注意的是,无论我们如何解读亚当斯论题P∗(A→B)=P(B|A)中的P∗,只要认为P∗是一元的分配函数(无论你称它为“概率”函数或是“可断说性”函数,或者主张A→B只能是简单条件句),都会成为壁花论证攻击的目标。因为,一元函数P∗对A→B给出的值,不会总是等于与之相对应的(二元)条件概率函数所给出的值。因此,哈耶克才说说:“更令人吃惊的是,简单条件句的可断说性会和条件概率并驾齐驱”([11],第158页)。 虽然Assa看起来像是直接在对一个语句分配可断说值,但它实质上是一个二元概率函数。对任何语句φ而言,Assa是对(φ为真,φ有真假值)去分配概率值,并把这个值视为是语句的可断说值。为了更加厘清此点,让笔者从另一个角度来分析Assa和一元概率函数间的不同。我们可以看到,刘易士、史东内克和哈耶克在看待语句S的概率时,都是从S为真的世界所分配到的概率值加总而来,而每一个世界所分配的概率值,实质上都是从一元概率函数而来,因为每一个世界的概率值,就是所有那个世界为真的语句所形成的连言句为真之概率。这也是为何一元概率函数对每个语句的分配值必须符合概率总和论题,因为语句S是它为真的世界之集合,因此,S为真的概率是它为真的世界之概率总和。然而,可断说性函数没有这样的特性,可断说性函数是在语句的概率值被分配之后,再去条件化语句的概率值来得到可断说值,换句话说,可断说函数没有对世界分配可断说值,所以可断说性函数不会有可断说性总和论题。 简言之,一元概率函数对语句所分配的概率值,来基于它对世界所分配的概率值加总而来;二元概率函数对语所句分配的值,是去条件化一元概率函数的概率值而来,而不是来自于它对世界分配了可断说值加总而来。因此,笔者认为[28]要避免贫乏性结果的重要关键在于,要去明确地区分一元概率函数和二元概率函数这两者之间的不同。 哈耶克也许已了解到这样的区分可以绕过贫乏性结果的攻击,不过他质疑我们需要可断说性这样的条件概率函数,哈耶克坚持的是,非条件概率函数就足以帮助我们去打赌条件句,条件句不需要可断说性这种二元函数([11],第157页)。遗憾的是,哈耶克并没有具体指出光凭非条件概率函数,如何帮助我们去打赌条件句。而[28]则是试图论证二元概率函数才能帮助我们理解如何去打赌条件句,我们可以把Assa视为是某种特别的条件概率函数,它把语句没有真假的世界之概率值照比例分配给该语句有真假值的世界,以这样的方式帮助我们得到打赌语句的公平赌率。 论文[28]论证了在计算语句的公平赌率时,我们是去衡量该下多大的赌注,对二值语句来说,我们能够拿回赌注的机会只有赢的时候,所以我们可以将公平赌率等同于赢的概率,也就是它为真的概率。可是,对于打赌条件句来说,当它没有真假时,我们也可以拿回赌注,但这并不是我们“赢”的情况,因此这部分的概率值不能纳入为真的概率。正如贫乏性结果给我们的教训,在处理和条件句相关的语句时,不要把Assa这样的条件概率函数当做是指派语句为真的概率。条件概率被视为打赌简单条件句的依据得到不少人的支持([8,16,23–25]),本文支持的(AT)是基于打赌简单条件句的方式,显示条件概率能指引我们去打赌条件句,这说明了为何条件概率会在条件句上扮演如此重要的角色。 亚当斯论题似乎攫取到条件句中一个相当重要的面向,但由于贫乏性结果,我们在解读亚当斯论题时要非常小心,以免有类似的结果。一个支持A→B有真假值的人,得支持概率总和论题而去驳斥(SH),但这不代表他得去驳斥亚当斯论题。本文支持[28]为亚当斯论题提出的解读,主张亚当斯论题应该被理解为(AT):简单条件句A→B的可断说等于条件概率P(B|A)。并详细地说明这样的解读如何避免贫乏性结果,不同于亚当斯,笔者论证这样的解读不需要去否认条件句有真假值,这显示条件句有真假值和亚当斯论题并不是互相冲突的立场。这样的进路也不同于苏庆辉([29]),不需要舍弃经典概率去避免贫乏性结果。16[28]中对条件句的理论虽然是三值语意论,但其中对条件句的概率之定义最终是化约到经典概率理论,使得经典概率理论可以去处理像条件句这样的三值语句。 如笔者在第二节指出,本文之所以讨论爱君腾和哈耶克对贫乏性结果的诊断是因为意识到,光是各别地去解决刘易士的四个贫乏性结果(或其它后继者的贫乏性结果)并无法全面性的解决贫乏性结果,还是会让人怀疑有不同的方法可以导出类似的结果。如近年来反对贫乏性结果的研究主要是针对刘易士的证明,如培根(Andrew Bacon)、何曼斯(Ronnie Hermens)和科祖克汉(Theodore Korzukhin)都想从脉络的角度下去质疑刘易士四个贫乏性结果所做的预设([4,12,18]),但他们都无法提出一个全面性的说法来证明条件句的机率一定会等于条件机率。例如,培根主张在脉络主义下,条件句的机率需要考虑两个证据,第一种证据是决定当前谈话的脉络下条件句所代表的命题;第二种证据是在决定我们如何判断这个条件句命题的机率。培根所主张的是“当这两个证据等同时,条件句的机率和条件机率会相符”([4],第134页)。何曼斯则是对路易斯的条件化函数提出许多反对,指出路易斯的条件化函数有些不合理的地方。他也对哈耶克的论证提出类似的质疑,并试图引进脉络的概念去找到一个好的条件化函数,使得它在满足史东内克假说的条件下,能满足一些合理的限制。 这样的进路虽然让史东内克假说在脉络主义下稍微获得喘息的空间,但仍无法完全摆脱贫乏性结果的阴影。因为,爱君腾和哈耶克的诊断所强调的是,用条件机率来定义一个命题为真的机率是很有问题的,这样的问题来自于条件机率本身所具有的特性,使得它似乎无法用来定义特定一个命题(不管是不是条件句)为真的机率。而这似乎是和脉络无关的,也和采取何种条件化函数无关,而是一个更根本的机率哲学问题,这才使得贫乏性结果对亚当斯论题和史东内克假说造成极大的难题。 有鉴于此,笔者认为一个更好的进路是对条件机率函数提出实质的说法,说明它为何会在条件句中扮演如此重要的角色,才能让我们对贫乏性结果毫无悬念。[28]对亚当斯论题的解读立基于三值语意学和打赌条件句的方式,试图提出一个一致性的概率理论与可断说性理论,但还是没清楚说明如何避免贫乏性结果。本文解决的方式是针对市面上的贫乏性结果找出共同的根源,论证[28]中的说法在进一步的厘清后,的确可以解决目前的困境,而且笔者提出的方法也可以适用于类似的理论。 然而,未来会不会有更精妙的贫乏性结果出现呢?笔者不敢保证。笔者想要强调的是,把条件句视为三值语句这个选项长久以来被忽略,也缺乏一个系统性的理论,这使得[28]这样的结合有许多细节仍需更进一步地讨论。笔者论证至少在贫乏性结果这一块拚图上,[28]的理论就目前看来是可行的,因此认为这是一个值得发展的方向。至于贫乏性以外的结果,并不在本文讨论的范围之内,笔者也无法在此做更进一步地评论。所以,笔者结论,就现今来说,(AT)是亚当斯论题最佳的解读,使得条件句有真假值与亚当斯论题可以并存不悖。 附录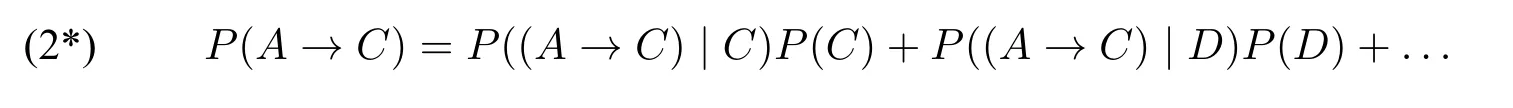

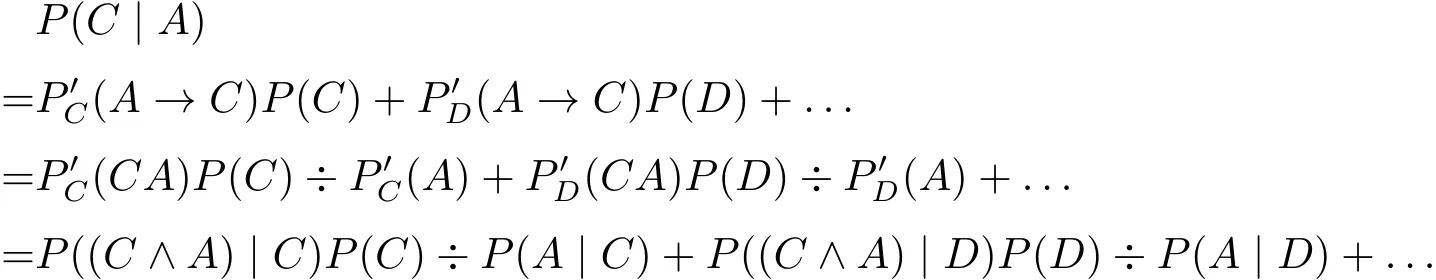

4 刘易士的最后一个贫乏性结果与壁花论证


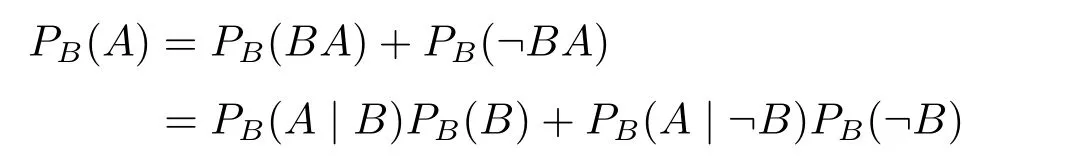
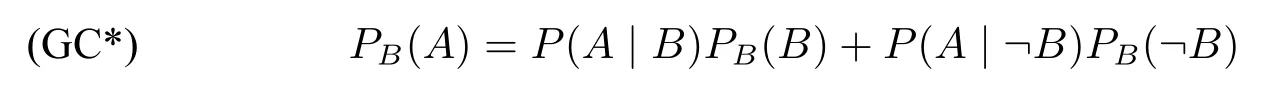




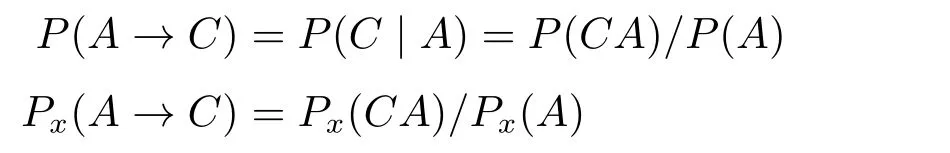




5 贫乏性结果的根源


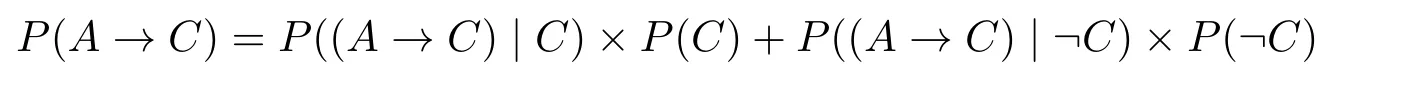

6 如何避免贫乏性结果








7 结语



