试析普莱尔基于混合时态逻辑对其时间观的辩护*,†

郭美云

西南大学逻辑与智能研究中心

guomy007@swu.edu.cn

1 导言

普莱尔（A.N.Prior,1914–1969）被认为既是时态逻辑的创始者，又是混合逻辑（Hybrid Logic）的创始者（[1]，第58页）。普莱尔根据其对时间的哲学思考，接受了麦克塔加（McTaggart）关于时间A-理论和B-理论的区分，认为A-理论中“过去、现在和将来”等概念比B-理论中的“在先、在后和同时”等概念更为基本，并且不承认时间点（Instants）的本体论地位（后文将详细论述）。因此，他在提出时态逻辑的同时，就给自己确立了一个哲学目标，即将B-理论中的时间概念用A-理论中的时间概念来表示，这在技术上表现为将无时态的一阶逻辑归约到时态逻辑中去。我们知道，基本时态逻辑的语言表达力是严格弱于一阶逻辑的。普莱尔所能采取的唯一途径就是不断扩张时态语言，他所采取的革命性手段是将表示时间点（可能世界语义学中的可能世界）的专名（Nominal）当作命题引入到时态语言当中，同时与全局模态词（Global Modality）结合，从而在逻辑语言中实现将B-理论中的时间概念归约到A-理论中的时间概念的哲学目标。正是在这种一阶逻辑和时态逻辑的牵涉或缠绕（Involvement）过程中，普莱尔提出了混合逻辑。但是，这两种概念可以相互表达，是否就意味着哪种概念更为基本？将时间点的名字作为命题是否就可以不承认时间点的本体论地位？本文在对普莱尔的辩护过程进行细致分析的基础上，从现代模态逻辑对应理论的角度指出，普莱尔对其时间观的辩护其实并不成功，并对普莱尔的方法论带给我们的启示予以讨论。

2 普莱尔的时间观

时间问题是贯穿于哲学史中的一个基本问题，很多哲学理论都依赖于对时间的不同理解或假定，如柏格森和海德格尔等人的哲学，这在西方哲学史上有很多讨论（关于时间哲学的讨论，可参考[6,8]）。普莱尔作为时态逻辑的创始人，对时间的一些基本问题做过深入思考，并形成了他自己关于时间的哲学思想。

普莱尔的时间观深受麦克塔加关于时间A-系列和B-系列理论区分的影响。麦克塔加在《时间的非实在性》一文中关于时间A-系列和B-系列的区分和讨论在哲学史上产生了巨大影响。麦克塔加认为，“按照时间显现给我们的初步印象，时间的位置可以区分为两种方式。每一时间位置都有相对于其他位置的在先或者在后（笔者注：后面称为B-时间系列概念）。并且每一时间位置也具有过去、现在或将来（笔者注：后面称为A-时间系列概念）。前者层级的区分是永恒的，而后者则并非如此。如果M曾先于N的，那么它就总是在先。可是，对一个事件而言，会有现在时态的现在、过去时态的将来和将来时态的过去的区别。”（[7]，第458页）

麦克塔加将描述时间的概念区分为A-系列和B-系列。它们分别涉及的基本概念如下：

A-系列：过去、现在和将来；

B-系列：在先、在后和同时。

A-系列时间认为，任何事件（Event）总是从遥远的过去到贴近现在的过去再到达现在，然后从现在到贴近的将来和遥远的将来，即时间总是有一个相对于“现在”的位置，或者为过去，或者为现在，或者为将来。因此这是一个动态的、局部的时间观。

B-系列时间观则认为，任何两个事件或者同时发生，或者一个事件在另一个事件之前，或者在另一个事件之后，这种先后关系是固定不变的。因此，B-系列时间是一种静态的、全局的和无时态（Tenseless）的时间观。

麦克塔加在做出上述区分并进行分析论证后认为A-系列时间和B-系列时间都是非实在的并且“我坚信时间是非真实的”（[7]，第457页）。麦克塔加关于时间A、B-系列的立场引起了很大的争议，后来的分析哲学家甚至因其立场不同分为A-理论家和B-理论家。A-理论家和B-理论家围绕麦克塔加论证的争论和反驳一直持续不断。不管怎样，麦克塔加关于时间A、B-系列的区分产生了巨大影响，“他一方面提供了探讨时间问题的基本论域（A-系列和B-系列）；另一方面是否定了时间的实在性，这是不得不面对的疑难。”（[12]，第86页）

麦克塔加关于时间A-理论和B-理论的区分深深地影响了普莱尔的时间哲学观，仅在论文集[11]中直接提到麦克塔加就多达11处之多，并且他直接表明了他支持A-理论时间的立场。

迄今为止，如果我有所谓哲学信条（creed）的话，它首先是：我相信关于过去、现在和将来的区分的实在性。我相信我们看到的事件的进程是一件接着一件的，而不象是一件所有事情永远粘在上面的无时间的织锦……（[10]，第1页）

因此，普莱尔持有一种动态时间观并且认为变化是与事件紧密联系在一起的。

普莱尔本人并未给出他对麦克塔加论证的直接反驳或者对其观点的哲学论证，现在一般认为，普莱尔之所以持有上述观点，这与他“一直致力于寻求一种极限决定论（Limit Determinism）以便为人类自由留出一些概念上的空间”（[4]，第3405页）紧密相关。

过去和未来的一个最大不同在于：一旦一件事情发生了就让我们够不着而成为过去，我们无法让它不再发生；而未来在某种程度上，尽管有时可能在很小程度上，我们可以发挥作用……（[10]，第2页）

正由于此，受克里普克信件的启发，普莱尔后来致力于分支时间逻辑的研究。更进一步地，普莱尔明确反对把时间孤立出来看作是实在的客观对象，即不同意将时间点或者说时刻（Instant）作为客观存在的对象或实体（Entities）的观点。

象“时间将有一个终点”，“时间是循环的”，“时间是连续的”等这样的陈述，如果从字面上看，暗示存在某个称作时间的巨大对象，它的各个部分如此这样排列着的（一个普遍的想法是时间象一根绳子，事件象珠子一样装结在上面）。但是当这些陈述被解释为一些不提到任何这类实体的陈述的缩写的时候，这些陈述就不再带有这样的暗示，而只是说什么事情将会是这样的，等等。（[9],第75页）

事实上，普莱尔不止一处表明自己的这一观点，除了后面讨论第一层级缠绕时提到外，他还进一步表明自己研究时态逻辑主要是出于对哲学形而上学的原因。

……因为我发现自己非常不能够将“时刻”（Instants）”严肃地当作个体实体（Individual Entities）；我不能理解时刻和时刻之间的早晚关系，除非它们是作为时态事实（Tensed Facts）的逻辑构建。时态逻辑对我而言，如果我能用一个习惯用语的话，那会是形而上学基础性的（Metaphysically Fundamental），而不仅仅是关于早晚关系的一阶逻辑的人为撕扯出来的一个片段。（[11]，第232页）

总之，尽管普莱尔的时间观在哲学上还有待于进一步考察，普莱尔在支持A-理论时间的哲学立场和反对将时间看作是实在的客观对象这两点是明确的。

3 普莱尔对其时间观的辩护

普莱尔对其时间观的辩护所使用的工具就是他所创立的时态逻辑，即创立一个用过去、现在和将来等基本时间概念构造一个关于A-理论时间的逻辑系统。普莱尔非常重视语言的逻辑分析，这也是他的主要分析工具和研究方法。普莱尔甚至认为语法师（Grammaticist）这一称号比分析师（Analysts）更适合自己（[11]，第11页）。自然语言为普莱尔分析时间概念和时态推理提供了大量丰富的素材。

3.1 自然语言中时态现象的逻辑分析

普莱尔首先通过对自然语言中时态语句的逻辑分析，将“过去”、“将来”等时态算子分析出来。具体方法是通过逻辑分析将时态语句改写为逻辑等值的句子，从而将时态算子显现出来。例如：

(1)It will be raining.可改写为：It will be the case that it is raining.

(2)It was raining.可改写为：It was the case that it is raining.

(3)It has been raining.可改写为：It has been the case that it is raining.

(4)It will always be raining.可改写为：It will always be the case that it is raining.

用Pp表示“命题p在过去的某个时间点上为真”，Fp表示“命题p在将来的某个时间点上为真”。如果用p表示“it is raining”，上述(1)、(2)两个命题则分别可以表示为Fp和Pp。用Hp表示“命题p在过去一直成立”，Gp表示“命题p在将来一直成立”，则上述(3)、(4)两个命题则分别可以用Hp和Gp表示。

由于“命题p在过去一直成立”和“并非命题p在过去某个时间不成立”是逻辑等值的，而“命题p在将来一直成立”和“并非命题p在将来某个时间不成立”是逻辑等值的。因此，Hp可被定义为“¬P¬p”，而Gp可被定义为“¬F¬p”，即H算子和G算子是不必要的，我们只要有过去算子和将来算子，就可以将它们分别定义出来。

采取这种前缀记法将时态处理成逻辑算子的优势在于，我们可以通过算子的组合和重叠将一些更为复杂的时态命题很容易地表示出来。例如过去完成时、过去将来时和将来完成时等。

(5)I had finished my paper.

(6)I will have finished my paper.

用p表示“I finish my paper.”，(5)、(6)可分别表示为PPp和FPp。

因为A-理论时间哲学家们往往认为只有“现在”才是真实的，过去和将来的时间都不是实在的。因此，在这个意义上，A-理论时间哲学家又被称作“现在主义者”（Presentism）。关于“现在（Now）”的分析比较复杂。因为，一方面“现在”或者说“当前”总是变化的、相对而言的。另一方面，命题p本身就可以看作是表示现在为真的命题，即用来谈论命题p的时间点就可以认为是“当前”，这也是一部分哲学家和逻辑学家认为“现在”是冗余（Redundant）的重要原因。但是，如果没有“现在”算子，当在自然语言语句中遇到从现在出发谈论过去或将来之后需要重新提及原来当前点的时候就会遇到困难，坎普（H.Kamp）就曾提出关于“现在”算子的二维语义学（[5]），并成功证明了在命题语言层次上，现在算子是冗余的，但在与量词有相互作用的情况下，则不是冗余的。受坎普工作的启发，普莱尔后来还曾专门写过一篇题为“现在”的论文（[11]，第171页），试图不用二维语义学而用混合逻辑的手段来处理“现在”算子。普莱尔通过在语言中直接用一个特殊的专名来表示“现在”，这可以看作是一种显性的处理方式。

3.2 时间概念的相互归约和表达

在Tense Logic and the Logic and of Earlier and Later和Tensed Proposition as Predicates两篇文章中，普莱尔从他的时间哲学思想出发，正如奎因（W.V.Quine）提出“模态缠绕的三个层级”一样，他提出时态-逻辑（Tense-logical）四个层级的缠绕（Involvement）。

普莱尔首先区分了时态命题（Tensed Proposition）和无时态命题（Untensed Proposition）。所谓时态命题就是真值依赖于某个时间点的命题。例如It is raining.I am having my breakfast.这类命题。反之，就是无时态命题，如1+1=2这类命题。普莱尔进而认为，时态命题是普遍的，无时态命题恰恰是时态命题的一种特例，即在相对于所有的时间点而言，它们的真值都是恒定的。

正是在这四个缠绕的讨论过程中，普莱尔提出了混合时态逻辑，而他之所以这么做的原因正是试图将关于时间B-理论的概念归约到A-理论的概念。

第一层级的缠绕。普莱尔用Ta(p)表示“命题p在时间点a上成立”（现在一般用@i表示Ti，命题@ip表示命题p在时间点i上为真。@i在混合逻辑中常被称作满足算子），用Uab表示a时间点早于b时间点，或者说时间点b晚于a时间点。显然Uab属于B-理论概念。“命题p在时间点a上成立”这一事实也是不会随时间变化而发生变化的，因此，普莱尔将Ta(p)也称为无时态（Tenseless）命题，即它也是B-时间理论中的概念。在第一层级的缠绕中，普莱尔发现A-理论和B-理论中的时间概念通过以下等式缠绕在一起。

即命题p在过去为真当且仅当命题在现在先前的某个时间点上为真；命题p在将来为真当且仅当命题现在之后的某个时间点上为真。

普莱尔意识到Ta算子可以充当翻译函数（今天在模态逻辑中称为标准翻译）的作用，如Ta(¬p)=¬Ta(p)，Ta(p→q)=Ta(p)→Ta(q)，其中Ta(p)在一阶逻辑中又可以表示为Pa，即时态命题p可以处理为一元谓词P，而时间点成了谓词中的变项。这样，通过一步步翻译，最后所有的时态命题都可以转换成用一阶逻辑语言表示的无时态命题。普莱尔发现，目前为止，Ta算子的作用仅仅在于将谓词附着在它的对象上，而这完全可以通过并置（Juxtaposition）的方式并使用括号来表示，如(¬p)a=¬(pa)等，即Ta算子没有发挥“在（at）”的作用，仅仅充当了“……的（of）”的作用，普莱尔把这称为第一层级的时态-逻辑缠绕。

而且正相反，通过翻译，极小时态逻辑成了一阶逻辑的副产品，A-理论中的时间概念竟都可以用B-理论中的时间概念表示出来。这是普莱尔的时间观所不能接受的，他批评道：

U-演算（笔者注：普莱尔提到的U-演算基本相当于关于时间先后关系的一阶演算）在哲学上并不比实质的时态逻辑在哲学上更简单。一方面它有两种不同类型的变元，而时态逻辑只有一种。如果说额外的变元仅仅是名字变元（name-variables），它们迟早要被引入的话，那么我回答是，它们是一类非常古怪实体的名字。至少对于我们更愿意看到“时间点”、“时间序列”应该仅仅是时态事实的逻辑构建的这些人而言。（[11]，第120页）

因此，普莱尔一方面出于时间形而上学哲学观的需要，另一方面也为了捍卫他所创立的时态逻辑的独立地位，他并不满足于此而止步不前，而是希望通过不断扩张时态逻辑语言的手段，将体现他的时间观的时态逻辑推进得更远。

第二层级的缠绕。在第二层级中，普莱尔从Ta算子入手，发现Ta(p)并不能完全等同于Pa，因为算子可以做不止一次运算，得到如Ta(Tb(Tc(p)))这样的公式。这正是将它处理为逻辑算子的优势。普莱尔进一步发现Ta算子有以下规律：

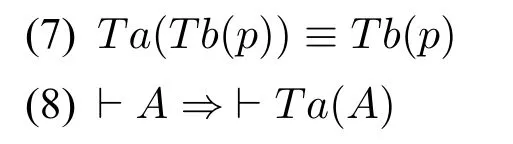
(7)表示命题p在时间点b上为真这一事实在任何其他时刻点上都是不会改变的。(8)则表示如果A是逻辑定理，那么它在任何时刻点上都是成立的。(8)加上之前的逻辑规律Ta(p→q)=Ta(p)→Ta(q)表明Ta算子还是模态逻辑中一个正规算子。

然而，既然将T作为逻辑算子形成命题，那它就与时态命题Pp、Fp和量化命题∀aTa(p)（∀aTa(p)表示命题p在所有的时间点上都为真）具有相同的地位，可以通过形成规则形成诸如((∀aTa(p)→Ta(p))→¬p)等更多公式。普莱尔用全局模态词2p表示∀aTa(p)，则显然有以下逻辑规律：

如果将Ta算子和2算子同时加入到U-演算（普莱尔将T算子加入到U-演算是为了使一阶演算更具有一些时态的特点。）中，则在U-演算中对于任何以T算子开头的定理Ta(A)而言，根据全称量化规则有∀aTa(A)，又根据(9)有A。因此，在U-演算中所有以Ta开头的具有时态意味的逻辑定理都可以证明为不带T算子，他将其称为第二层级的缠绕。普莱尔据此认为，这使得U-演算和时态逻辑不再仅仅具有平行的意味，时态逻辑现在表现为U-演算的一部分，这可以为他将U-演算当作时态逻辑的一部分准备道路（[11]，第122页）。

第三层级的缠绕。第三层级的缠绕是普莱尔达成其目标的关键一步，也正是这一步使得他创立了混合逻辑。这关键一步是引入一类特殊的变元，引入一些特殊的变元作为非严格指示词来表示时间点（或者说时刻点）1时间点在可能世界语义学中就是可能世界，将可能世界的名字引入到模态语言，从而能够谈论可能世界本身，这是混合逻辑诞生的关键一步。，并将它们直接作为命题加入到时态语言当中，例如用命题a表示当前时间点的名字是a，用Ta(b)表示在a这个名字表示的时间点的名字也是b，即a、b两个名字表示同一个时间点。这种表示在自然语言中是很常见的，例如我们总是谈论现在是几月几号甚至几分几秒等等。但这并不意味着普莱尔将时刻点当成实体，为此他辩护道：

我们可以，例如，将时刻点等同于在该时刻点成立的所有命题的合取，或者将它看作是仅仅在该时刻点成立一种特殊命题，即是它的索引词（Index）。（[11]，第124页）

把时刻点作为一类特殊的命题引入到时态逻辑之后，借助于全局模态算子2，我们就可以定义出T算子，进而将U关系这样的时间B-理论概念用A-理论概念表示出来。

根据(11)和(12)，有Uab=2(a→Fb)（或者Uab=2(b→Pa)）。即a在b之前当且仅当如果当前时刻点为a的话，那么在将来有b时刻点。甚至还可以表示B-理论时间概念中的“同时”这一概念。如用Iab表示时刻点a和b同时，可表示为2(a↔b)。

从一阶逻辑的观点看，将可能世界的名字引入到时态语言中，就是将一阶语言中个体的名字即常项和等词引入到了模态语言中。从翻译的角度看，时态公式Ta(b)可翻译为一阶公式a=b。事实上，现在的研究表明，带有可能世界名字和全局模态算子、满足算子的模态语言的表达力和带等词的一阶逻辑是一样的（[3]，第2页）。因此，经过上述扩张之后的时态混合逻辑语言可以全部表达B-理论中的时间概念也就不足为奇了。

第四层级的缠绕。在第四层级中，普莱尔在第三层级的基础上进一步在时态逻辑语言中消除全局模态算子。首先，在时间序列是独一无二、不分叉且时间先后关系具有传递性的假设下，全局模态算子可以通过时态算子定义如下：

即“p在所有时间点上为真”当且仅当“p为真且p在过去一直为真且p在将来一直为真”。其次，在仅仅假设时间序列是独一无二的假设下，全局模态算子还可以通过以下方式定义：

普莱尔表明，通过加上量词的相关规则，可以证明现在定义出来的2算子具有先前全局模态算子的性质和特点。

于是，在第三和第四层级中，普莱尔通过引入时间点的名字作为一类特殊的命题的方式，并将其与全局模态相互作用，就可以仅仅使用“过去”（P算子）和“将来（F算子）”这些A-理论时间概念作为初始概念，定义出“命题在某时间点上为真”（T算子）和“时间的先后关系”（U关系）这些无时态命题所表达的B-理论时间概念。

3.3 重新回到自然语言和模态逻辑

传统的模态语言（Orthodox Modal Language）有一个重要的缺陷，就是它不能谈论可能世界本身，即可能世界没有名字。虽然说话的时间点和事件发生的时间点在传统模态语言中可以表示出来2例如一个过去式句子“特朗普当选了美国总统”，在传统模态语言中可用Pp表示。事件发生的时间点通过P算子在语言中得到明确表达。因为传统模态逻辑已有局部（Local）的特点，用来评估这一命题真假的时间点就可以表示出说话的时间点。，但提及的时间点在传统模态语言中是无法表示的。这样，就不能在传统模态语言中明确讨论某个特定的时间点发生了什么事件。这在涉及时态推理的时候表现得尤为明显。

根据赖欣巴哈（H.Reichenbach）在自然语言的时态语义中区分的三种时态点（Temporal Reference），一种是说话的时间点（Speech time），一种是事件发生的时间点（Event Time），还有一种是提及的时间点（Reference Time）。例如一个将来完成时句子，“在2020年之前我就已经完成了书稿”。其中涉及到三个时间点，它们的顺序依次是，说这句话时的时间点，完成书稿的时间点，以及提及的时间点即2020年。上述将来完成时的句子很容易用混合时态逻辑语言形式化为F(a∧Pp)。正如P.Blackburn强调的，普莱尔这种基于算子的混合逻辑方法可以将自然语言中的各种时态语句用一种统一的形式表示出来，并且可以回答语言学家们对H.Reichenbach所使用的表示方法的批评（[2]，第3687页）。因此，混合时态逻辑在自然语言中应用值得进一步研究。

正因为可能世界没有名字，传统模态语言接下来的一个重要的缺陷是，它不能断定两个可能世界是同一个可能世界，而这在一些实际应用中是很有用处的。例如通过两个不同的进程最后到达的可能是同一个可能状态。可能世界有了名字之后，两个可能世界是同一个可能世界很容易用普莱尔的混合逻辑语言表达为Ta(b)。事实上，普莱尔在上述辩护过程中创立的混合逻辑极大地提高了传统模态语言的表达力，传统模态逻辑框架上不能定义的禁自反性、不对称性和反对称性等在混合逻辑中都可以定义出来，并且有一些混合逻辑并没有破坏模态逻辑语言局部的特点和优势，从而保持有穷模型性和可判定性等模态逻辑所原来具有的良好性质（[3]）。这也是混合逻辑在人工智能中知识表示3后来发现人工智能中用来描述网络本体的描述逻辑（Description Logic）本质上正是混合逻辑。和计算语言学中有广泛应用的重要原因。

4 对普莱尔辩护的评价及其启示

普莱尔从自己关于时间的哲学立场出发，致力于将B-理论的时间概念归约到A-理论的时间概念中去，所采取的逻辑技术手段是将一阶逻辑的语言翻译到时态语言中。我们知道，基本时态语言（仅有将来和过去算子）的表达力是严格弱于一阶语言的。于是，普莱尔唯一的出路就是如何扩张时态语言。他所采取的一个革命性手段就是在第三层级缠绕中将可能世界的名字作为命题引入到时态语言中，加上全局模态词从而使其具有和一阶语言一样的表达力。有意思的是，这一过程既是对他的时间观的辩护，也是他为自己所创立的时态逻辑的辩护，因为如果时态逻辑仅仅是一阶逻辑的一部分或者副产品的话，那么和模态命题逻辑相比，时态逻辑所具有的独立地位也就变得岌岌可危。

然而，普莱尔利用混合时态逻辑对其时间观的辩护并不成功。首先，从现代模态逻辑中对应理论的观点来看，无论是基本时态语言、混合时态语言还是一阶语言，它们的框架都是(T,B)，其中T表示时间点的集合，B表示时间的先后关系。它们都是用来描述和表达这同一框架（严格说是时间框架）的不同逻辑语言，这些语言可以相互归约并不能说明哪一种时间概念更为基本或初始。其次，框架和模型是逻辑语言所共同讨论的对象，可以看作是世界的本体（Ontologies），从这个角度讲反而是对时间B-理论的支持和辩护。不管怎样，笔者认为，至少在我们的思维领域中，B-理论时间概念依然是我们关于时间这一抽象结构的基本概念。最后，普莱尔自己后来也发现，如果将他所提出的时态混合语言用于描述人，将U关系解释为人之间的高矮关系，那么他所得到的逻辑4普莱尔将其称为“自我中心的逻辑（Egocentric Logic）”是一样的。如果普莱尔拒绝将时间点当作客观存在的实体的话，那么他不得不也拒绝将人当作客观存在的实体，从而陷入了困境（[11]，第232页）。因此，他所创立的时态混合逻辑在哲学上是中立的，并不能为普莱尔关于时间的形而上学观念提供任何支持。

尽管普莱尔对其时间观的逻辑辩护并不成功，也就是说，他并没有达到他的哲学目标，但是并不影响他的逻辑成就与贡献，在这一过程中他意外地得到了一种新的逻辑——混合逻辑。普莱尔作为混合逻辑的创始者，其动机虽然是出于关于时间形而上学的考虑，其技术本质却是将可能世界和满足算子等这些原本属于语义的元素输入到逻辑语言之中给以明确讨论，这不得不引发我们关于语言和语义关系或者说逻辑与元逻辑（Meta-logic）关系的重新思考。普莱尔作为时态逻辑的创始者，他试图为时间的跨学科研究提供一种精确的通用语言，对于今天人工智能知识表示中对时态信息的处理依然有重要的借鉴和启示作用。此外，普莱尔在时态区间逻辑（Interval Tense Logic或者Metric Logic）、分支时间逻辑（Branching Time Logic）和关于“现在”的逻辑的一些开创性工作还有待进一步研究和发展。

普莱尔是一名具有强烈哲学和形而上学关切的逻辑学家，他坚信逻辑在哲学以及其他各门学科中基础性地位和作用，一方面将哲学或自然语言中的各种概念在逻辑分析之后用逻辑的方法进行处理和研究，另一方面又将得到的新逻辑用于讨论哲学和语言中的问题。他的逻辑观和方法论对于我们今天从事逻辑的各种跨学科研究依然有着很重要的启示作用。此外，普莱尔从丰富的自然语言汲取的研究灵感以及时态逻辑给他带来的新视角，使得他对很多逻辑哲学问题有了新的理解和看法，正如他自己说的，“逻辑学家必须更象一位律师，……，他必须告诉他的顾客给定一个选择的后果是什么，……，他可以做的另外一个选择是什么；但是我怀疑作为一名逻辑学家，他是否还能做得更多”（[9]，第59页）。