工作流可满足决策（≠）的完备独立树分解回溯法*

翟治年，卢亚辉，余法红，高慧敏

1.浙江科技学院 信息与电子工程学院，杭州 310023

2.深圳大学 计算机与软件学院，广东 深圳 518060

3.嘉兴学院 数理与信息工程学院，浙江 嘉兴 314001

4.嘉兴学院 机电工程学院，浙江 嘉兴 314001

1 引言

工作流技术通过形式化建模与分析，实现业务执行的自动调度，在云制造、众包等平台中起着重要作用。工作流每个步骤有一个授权（资源）列表，某些步骤的执行资源之间须满足一定约束。所谓工作流可满足决策（workflow satisfiability decision，*WS）寻求满足授权和约束的任一资源分配解，可为业务正确执行提供最低限度的保证。由于互斥是广泛存在的职责分离等多种约束类型的特殊情形，并经常参与各种组合约束配置，故仅含互斥约束的*WS是一个基本问题，记为*WS（≠）。它具有NP完全性[1]，且实用中可能涉及多达上百个步骤，故其算法的理论和实际性能是研究社区关注的焦点。

WS（≠）的早期研究[2-4]中，求解方法均为各种形式的穷举搜索，时间复杂度通常为O*(|U||S|)级（U、S分别为资源集和步骤集），随着步骤集规模增长，实际性能下降很快。2011年，Basin等人对带选择分支的工作流研究了互斥和绑定约束下的*WS，并给出了一种多项式时间近似算法，但其依赖于大量资源和授权均匀分布假设，且某些有解的情况会被判定为无解[5]。2013年，Crampton等人将多种*WS（≠）归约为集合最大权划分，得到了小底数的指数时间复杂度，其*WS（≠）情形的时间复杂度为O*(2|S|(|X|+|U|2))[6]（X为互斥约束集），这是目前最好的结果。但其空间代价为指数级，严重限制了求解规模。2014年，Cohen等人识别了一大类约束的正规性或资源独立性特征，据此提出了模式编码技术，并给出了相应*WS的动态规划算法，其时间复杂度为O*(3|S|wlbw)，其中w是正规性等价关系关于资源集的分散度[7]，随后又针对资源独立性计数约束的*WS，给出了类似的算法[8]。2014年，Yang等人对考虑控制流结构的*WS进行了较全面的复杂性归类[9]，但未求解其中的NP难问题。2015年，Karapetyan等人将模式编码与回溯搜索结合，提出了*WS的模式回溯算法，在正规性约束下具有目前最好的实际性能[10]。2016年，Crampton等人将资源独立约束推广为类独立约束，给出了层次组织约束*WS的模式回溯算法[11]，其关于资源独立约束的退化情形即为Karapetyan的算法。对于资源独立约束，模式回溯算法的空间复杂度为O(|S|×|U|)，但其时间复杂度为O*(B|S|)，B|S|为第|S|个贝尔数[10]。由于B|S|的增长比2|S|和3|S|等指数函数快得多，上述结果仍然很不理想。总的来说，现有*WS（≠）研究取得了多方面进展，出现了一些代表性算法，但其对理论或实际性能、时间或空间优化往往会牺牲相对的指标，失衡情况严重，亟待研究综合性能良好的新型算法。

工作流可满足性是约束可满足问题（constraint satisfaction problem，CSP）在访问控制约束下的特殊情形。在CSP研究中，约束图树分解是保证理论性能的重要方法，可得到以树分解宽度+1为幂指数的时间复杂度。同时，回溯法深度优先和及时剪枝的搜索方式契合CSP寻找第一个可行解的问题性质，是其完备求解的主要方式。2003年，Jegou等人将两种技术结合，提出了树分解回溯（backtracking treedecomposition，BTD）的方法[12]，以兼顾理论和实际时间性能，但缓存造成了较高的空间复杂度。根据*WS（≠）的特点，本文拟利用BTD来解决前述性能失衡问题。这是因为：工作流约束用来表达关键性业务规则，其密度通常较低，有利于控制树分解宽度；BTD的回溯搜索有很大机会快速找到一个解，并由此避免缓存过度扩张。

然而，BTD在确定兄弟子问题的相互独立性时，仅以待赋值变量集之间的约束不相关性为依据，而未证明其变量不相交，无法保证子问题的解兼容。随后，BTD得到了不同角度的增强和应用，如2003年和2004年将BTD用于求解Valued CSP和Max-CSP问题的工作[13-14]，2007年关于BTD中变量排序规则的研究[15-16]，2009年将BTD应用于#CSP的#BTD算法[17]，2014年为包连通树宽概念给出树分解算法并将其引入BTD的工作[18]，2016年对#BTD的全局一致性改进[19]，2017年通过重启搜索来提高BTD性能的研究[20]，等等。这些变种算法研究均以BTD子问题独立性为基础，但未见指出其成立条件缺失问题，并给出变量不相关性证明，故BTD的成立基础仍比较脆弱，亟待进行相关的理论研究。

本文从低约束密度下的技术选型出发，通过深入BTD基本理论的研究，得到了*WS（≠）性能平衡问题的一种正确有效的解决方案，其主要贡献是：（1）从变量不相交和约束不相关两个角度提出了一种完备的BTD子问题独立性，克服了现有BTD不能证明子问题变量不相交的基本缺陷，进而给出了相应的部分解缓存原理。（2）通过逐级分解为独立子问题，并利用缓存避免重复求解，设计了一种WS（≠）决策算法，并通过交替归纳的方法证明其正确性。该算法时间复杂度为O*(|S|3×dW+1)，幂指数可小于步骤集规模，且在较低约束密度下实测性能突出。

2 预备知识

本章介绍CSP及约束网络树分解的概念。

定义1（约束可满足问题）CSP定义为四元组＜V,D,E,R>，其中：V是有限变量集，每个v∈V存在有限值域dv，D={dv|v∈V}，E是2V子集的多重集，表示约束集，每个e={v1,v2,…,vk}∈E有值域de⊆dx1&dx2&…&dxk（&表示无序卡氏积），而R={de|e∈E}。图＜V,E>称为该CSP的约束网络。

定义2（赋值与可行解）给定前述的CSP，对任何Y⊆V，称函数是Y的赋值。由于值域已确定，此函数可记为α:Y，若Y可由上下文确定，也可记为α。

若任取v∈Y，均有α(v)∈dv，则称α符合变量值域。若对任何e={v1,v2,…,vk}∈E且e⊆Y，均有{α(v1),α(v2),…,α(vk)}∈de，则称α符合约束值域。若α同时符合变量和约束值域，则其是合法的。整个V的合法赋值称为CSP的可行解。

按求解目标的差异，CSP分为三类：求任意一个可行解（或指出其不存在）的，称为CSP决策；仅判断可行解存在与否的，称为CSP判定（determining CSP）；求所有可行解个数的，称为CSP计数（counting CSP，#CSP）。

CSP的搜索求解可能用到以下概念：

定义3（赋值投影）给定赋值α:Y′，若Y⊆Y′，则α在Y上的投影α↑Y是Y的赋值，且任取v∈Y，有α↑Y(v)=α(v)。

定义4（赋值兼容）设赋值α1:Y1和α2:Y2均合法，若存在合法赋值α:Y1⋃Y2，使α↑Y1=α1且α↑Y2=α2，则称α1和α2兼容，否则称两者冲突。

定义5（赋值扩展） 设有赋值α:Y和α′:Y′，且Y⊆Y′，若α′↑Y=α，则称α′是α在Y′-Y上的扩展。显然，若α和α′都合法，则两者一定兼容。

为了分解约束网络的复杂性，介绍如下概念：

定义6（图的树分解）给定图＜V,E>，其树分解定义为二元组＜C,T>，其中T=＜I,F>是顶点集为I、边集为F的树，而C={Ci|i∈I}是V的子集族。因T的每个顶点i对应一个变量簇集Ci，＜C,T>可视作以C为顶点集的树。它满足以下性质：

（2）任取e∈E，存在i∈I使得e⊆Ci。

（3）任取i,j,k∈I，若在树T中k位于从i到j的路径上，则Ci⋂Cj⊆Ck。

W=maxi∈I|Ci|-1称为树分解的宽度。CSP的树宽w定义为其约束网络所有树分解的最小宽度。

对i,j∈I，约定：C(i)表示Ci各祖先结点的变量集，则C[i]=C(i)⋃Ci表示Ci及其祖先结点的变量集；sup(i)和subs(i)分别表示i的父亲和所有儿子；Desc(j)表示j及其所有后代，而。

3 工作流可满足决策（≠）

约定S表示工作流的步骤集，U表示其资源集。

3.1 问题定义

本节给出互斥约束WS决策问题的定义。

定义7（授权）授权A={UA(s)|s∈S}，其中UA(s)是步骤s的授权资源（即候选执行者）列表。

定义8（互斥约束集）互斥约束集X⊆S&S，表示步骤间的二元职责分离关系：若{s,s′}∈X，则对工作流的同一案例，s和s′的执行资源不能相同。

定义9（资源分配）资源分配π:S→U为工作流案例的每个步骤指派唯一的执行资源。

定义 10（*WS(≠)问题）*WS(≠)定义为四元组＜S,U,A,X>，须求任一资源分配π:S→U，使任取s∈S，π(s)∈UA(s)，任取{s,s′}∈X，π(s)≠π(s′)。

3.2 问题求解

3.2.1 BTD的子问题独立性缺陷

BTD的核心概念是如下描述的子问题独立性。

定理1[12]设图＜V,E>有树分解＜C,T>，其中T=＜I,F>，且I的先根遍历序列Γ=1,2,…,|I|。若i,j∈I,i＜j且i=sup(j)，则没有和v∈Desc(Cj)-Ci⋂Cj使得{u,v}∈E。

该定理表明：若删除Ci⋂Cj所含变量，则Desc(Cj)中各簇集所含剩余变量与Cj之前所有簇集所含剩余变量之间的约束联系将被切断。在此基础上，现有BTD导出了相应的子问题独立性关系。设j1＜j2＜…＜jq均为i的儿子，1≤p＜q，由定理1：Desc(Cjp)-的合法赋值不会因彼此约束而发生冲突。若Ci已合法赋值，则其每个儿子Cjk(1≤k≤p)代表的子问题（须为Desc(Cjk)-Ci赋值）可依次独立求解。然而，完成子问题求解后，须将相应部分解组合进父问题的部分解。若Cjp和Cjq相应子问题的变量集，即Desc(Cjp)-Ci与Desc(Cjq)-Ci，存在重叠变量v，则它们的独立求解可能对v赋不同的值，从而导致两个部分解冲突。

为保证BTD的正确性，约束不相关和变量不相交条件缺一不可。前者可由定理1加以保证，但后者尚未从理论上得到证明。由子问题独立性衍生的BTD缓存设计原理（见文献[12]引理1）也存在类似缺陷，即不能保证缓存部分解与其他部分解兼容。

3.2.2 新的BTD子问题独立性及其缓存原理

针对BTD的上述缺陷，本文将建立一种完备的子问题独立性。首先给出本文的基本定理。

定理2设i,j∈I，f={i,j}∈F，从T中删除f得到两个连通片Ti=＜Ii,Fi>和Tj=＜Ij,Fj>，其中i∈Ii，j∈Ij，则：

证明（1）用反证法。假设，则必存在p∈Ii和q∈Ij使得v∈Cp⋂Cq。由于Ti和Tj是T删除f所得两个连通片，因此p和q在树T中经f连通，即连通二者的路径经过i和j。由定义6（3）可知，Cp⋂Cq⊆Ci⋂Cj，从而v∈Ci⋂Cj，与矛盾。

任何变量簇集Ck都位于Ti或Tj之一，而Ci⋂Cj是两者的交界。该定理表明：（1）删除Ci⋂Cj中的变量，则剩余所有变量分为不相交的两部分；（2）这两部分之间无约束（易知（2）是定理1的推广）。这样，只有Ci⋂Cj的赋值才会影响的赋值。该定理有如下推论（设i,j∈I，且sup(j)=i）：

推论1

证明由于，只须证明Desc(Cj)-即可。反设存在v属于前者而不属于后者，则必有。由于，又有，与定理2（1）矛盾。

该推论表明确定C[i]、Ci或Ci⋂Cj的赋值后，对以Cj为根的子树，将得到同样的剩余变量集。由此可给出子问题的三种等价条件，其中第一种用于设计算法的递归结构，第三种用于部分解的缓存。

现在给出本文的子问题独立性概念，表述如下：

定理3设j1＜j2＜…＜jk为i∈I的所有子结点。若给定C[i]中所有变量的合法赋值，则任取1≤p≠不相交，且两者之间无约束。

证明设fp={i,jp}，则T-fp分为两个连通片，一个由导出，设为，另一个设为，则必有，即，则由推论1：

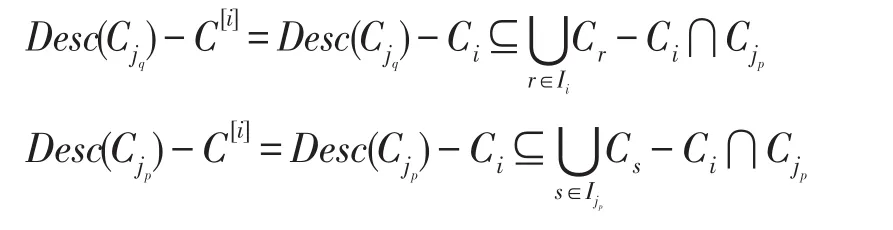
再由定理2即可导出本命题的结论。

该定理表明：在树分解中，当所有祖先结点中所含变量已合法赋值时，对两棵兄弟子树各自的剩余变量进行赋值，将是完全独立的子问题。若其都有与前提兼容的部分解，则可以无冲突地合并。这就为设计CSP的递归算法提供了依据。在C[sup(i)]合法赋值后，为求解Ci代表的子问题（对Desc(Ci)中剩余变量赋值），可先对Ci（中剩余变量）尝试赋值，对它的每一种（与C[sup(i)]兼容的）合法赋值，求解各子问题Cjt(1≤t≤k)。

由推论1，子问题Cjt的变量集Desc(Cjt)-C[i]=Desc(Cjt)-Ci⋂Cjt，而定理2表明，其赋值只受Ci⋂Cjt的赋值影响。于是，子问题Cjt仅以Ci⋂Cjt的赋值为条件。若Ci的不同赋值在Ci⋂Cjt上投影相同，则相应子问题Cj只须求解一次。进而，可建立如下缓存原理：

定理4设＜C,T>是CSP约束图＜V,E>的树分解，T=＜I,F>，i,j∈I，且sup(j)=i。又设变量集Y≠Y′满足Ci⋂Cj⊆Y,Y′⊆V-(Desc(Cj)-C[i])。若α:Y和α′:Y′均合法，且在Ci⋂Cj上投影相同，则有：

（1）α在Desc(Cj)-C[i]上有合法扩展，当且仅当α′在Desc(Cj)-C[i]上有合法扩展。

（2）设αX是α在Desc(Cj)-C[i]上的合法扩展，则αX↑(Desc(Cj)-C[i])与α′:Y′兼容。

证明（1）只证必要性，充分性类似。反设α′:Y′在Desc(Cj)-C[i]上无合法扩展。由定理条件可知Desc(Cj)-C[i]与Y′不相交，且由结论（1）左端不难得出Ci⋂Cj和Desc(Cj)-C[i]各自有合法赋值且两者兼容，故Desc(Cj)-C[i]与Y′-Ci⋂Cj之间必然存在约束。但Y′-Ci⋂Cj⊆V-(Desc(Cj)-C[i])-Ci⋂Cj=(V-Ci⋂Cj)-(Desc(Cj)-Ci⋂Cj)=(V-Desc(Cj))-Ci⋂Cj，由定理2（2）不难推出Y′-Ci⋂Cj与Desc(Cj)-C[i]=Desc(Cj)-Ci⋂Cj间无约束，矛盾。

（2）易知αX、α和α′在Ci⋂Cj上的投影均相同。由αX合法知该投影与αX↑(Desc(Cj)-C[i])兼容。又Y′-Ci⋂Cj与Desc(Cj)-C[i]不相交、无约束，故整个α′:Y′与αX↑(Desc(Cj)-C[i])也兼容。

该定理表明：不同前提下的子问题Cj是等价的，只要前提在Ci⋂Cj上的投影相同，且一个前提下的部分解与另一个前提兼容。在某个前提及相应Ci⋂Cj赋值下求出子问题Cj的部分解后，可将其写入缓存，若在新前提下求解子问题Cj，只要Ci⋂Cj的赋值相同，均可读取缓存结果，避免重复求解。

3.2.3 WS（≠）决策的BTD算法

本节基于上述理论建立一种新的*WS（≠）算法。目前已有工作将#BTD用于WS（≠）计数[21]，但其未从理论上识别和解决前述的独立性问题，算法的结果构造、搜索组织和缓存利用方式也不同于本文。下面给出本文算法的描述（因不同连通片对应独立的问题，只须考虑连通约束图）。

算法1*WS（≠）-BTD//A1

输入：α,Ci,Ri，其中Ci是＜S,X>树分解的当前结点，α是对C[sup(i)]中所有和Ci-C[sup(i)]中部分步骤的合法赋值，而Ri是Ci-C[sup(i)]的α未赋值变量集，故Dom(α)=C[i]-Ri。

输出：与α兼容的合法赋值β:Desc(Ci)-Dom(α)，或当其不存在时，返回β=NULL。β可看作单变量赋值的集合，故其为∅表示无剩余步骤须赋值。

初始调用为A1(α:∅,C1,C1)，C1为树分解的根。

若算法1是正确的，即其任何对满足输入要求的α,Ci,Ci，均可返回满足输出要求的β，则其对满足Dom(α)=C[1]-C1=∅ 的初始调用，若返回β:Desc(Ci)-Dom(α)，即为树中也是问题所有变量的一个合法赋值，若返回β=NULL，上述合法赋值必无解。该*WS（≠）算法的正确性已蕴涵其完备性。

为证明算法1正确，根据其结构特点，本文将分条件按两个值做归纳：（1）若Ri≠∅，按|Ri|做归纳，其基始为Ri=∅ 的情况，归纳假设定义于Ri的基数为|Ri|-1的真子集；（2）若Ri=∅，按Ci与其后代叶子的最小高差做归纳，基始为Ci为叶的情况，归纳假设定义于Ci的每个儿子。两种基始情况叠加即为整个证明的基始。若忽略约束满足要求，则任意待证情形都可还原至这一基始，只须交替向两种归纳假设针对的情形转化。对（1）的情况，连续转化至对应归纳假设，最终将变为（2）的情况，此时若当前结点Ci非叶，则向对应的归纳假设转化，将对其每个儿子，得到（1）的情形，如此交替，直至在每个叶子上都有Ri=∅。而若考虑约束要求，某些中间情形可能找不到合法赋值，此时可直接判定其无解，不必还原至基始。具体的归纳证明如下：

基始。Ci为叶且Ri=∅ 时，须验证A1(α,Ci,Ri)正确返回。此时，第2行返回∅ 。因β的定义域Desc(Ci)-Dom(α)=Ci-(C[i]-∅)=∅，返回正确。

归纳步骤。对Ci非叶或Ri≠∅ 的情况，目标是基于如下归纳假设，证明A1(α,Ci,Ri)正确返回：

（1）待证情形满足Ri≠ ∅ 时，假设任取s∈Ri，A1(α:C[i]-(Ri-{s}),Ci,Ri-{s})正确返回。

（2）待证情形满足Ri=∅ 时，若Ci为叶，则为基始情形，已验证成立；否则任取Cj∈subs(Ci)，假设A1(α:C[j]-(Cj-Ci),Cj,Cj-Ci)正确返回。

归纳步骤的证明如下：

若Ri≠ ∅，第22～33行将寻找s∈Ri，及其与α兼容的（合法）赋值s→u。若找到，由归纳假设（1），第 30 行调用 A1(α:C[i]-(Ri-{s}),Ci,Ri-{s})将正确返回。若β≠ NULL，则与 (α:C[i]-Ri)⋃{s→u}兼容，且其定义域为：

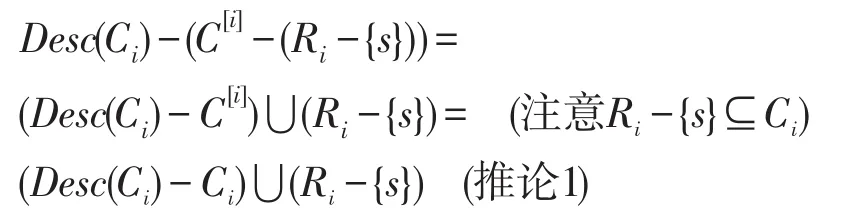
第31行为其附加s→u后返回，恰为(Desc(Ci)-Ci)⋃Ri的α:C[i]-Ri兼容赋值，因而正确。若穷尽UA(s)都找不到兼容的s→u，或者每次找到后第30行都返回NULL，则α:C[i]-Ri无合法扩展，从而第 34 行返回NULL也正确。

若Ri=∅，考查Ci。若其为叶，则落入基始情形。若其非叶，第4～19行对每个Cj∈subs(Ci)调用A1(αj:C[j]-(Cj-Ci),Cj,Cj-Ci)（或读取缓存），得到βj。由归纳假设（2），调用都将正确返回（而缓存是之前的调用结果），故所得βj都是正确的。若某个βj=NULL，则α:C[i]不可能有合法扩展，故第16行返回NULL是正确的。否则，每个βj都是Desc(Cj)-(C[j]-(Cj-Ci))的αj兼容赋值。由于C[j]-(Cj-Ci)=(C[j]-Cj)⋃(Ci⋂Cj)=(C[i]-Cj)⋃(Ci⋂Cj)（注意C[j]=C[i]⋃Cj）=(C[i]-Ci⋂Cj)⋃(Ci⋂Cj)（由定理 2（1）推导可知，C[i]⋂Cj⊆，有αj=α和Dom(βj)=Desc(Cj)-C[i]。由定理3，各Dom(βj)不相交，无约束，故第19行返回是（注意且Ci⊆C[i]）=Desc(Ci)-(C[i]-∅)的α兼容赋值，是正确的。

综合基始与归纳步骤，算法1是正确的。

算法1的时间代价分为三部分：（1）每个结点内的回溯搜索（第22～32行）。（2）整体结构上深度优先处理相关代价，包括取下一子结点（第6～8行），合并子问题部分解（第15～17行）。（3）缓存查找（第9行）和插入（第13行）。各自分析如下：

（1）由于缓存的使用，相应于Cj⋂Ci的每一合法赋值，对Cj-Ci的回溯搜索至多执行一次，故每结点内的回溯搜索至多执行一次。每个结点所含变量至多W+1个，其值域大小至多，又每个变量至多与|X|-1个变量互斥，每次赋值后至多验证min{|X|,|S|}个约束，而结点数为O(|S|)，故这部分的总代价为O*(|S|2×dW+1)。

（2）由于深度优先处理可能回溯到父结点和重新进入子结点，每个结点可多次到达，但次数不超过其父结点局部解空间的大小（只有父结点被搜索时，才可能进入其子结点，而父结点至多执行一次完整的回溯搜索），即为O(dW+1)次，每次到达需要取该结点的所有儿子，所有子问题递归调用结束后执行部分解合并，均需要O(|S|)代价，由于总结点数为O(|S|)，这部分的总代价为O*(|S|2×dW+1)。

（3）对树分解每条边对应的割集，设一个平衡二叉查找树作为缓存，割集大小即关键字比较代价，不超过，每一缓存的关键字数量为O(dw)个，读取/写入一个解的代价为O(|S|)，故每次查找/插入代价为O*(|S|wlb(dw))，又每个缓存可被访问O(dW+1)次（子结点到达次数），故这部分的总代价为O*(|S|×dW+1wlb(dw))=O*(|S|3×dW+1)。

综上知算法1的时间复杂度为O*(|S|3×dW+1)，因(W+1)/|S|不超过1且可能相当小，若d也较小则可优于文献[6]的O*(2|S|(|X|+|U|2))时间。

算法1的空间代价主要是缓存，由前述分析，每一缓存占O((w+|S|)dw)=O(|S|×dw)空间，而缓存个数或割集数为O(|S|)，故总的空间为O(|S|2×dw)。

4 实验研究

本章对算法1的性能进行实验研究。本文和对比算法均以C++实现，并使用GMP算术库处理大整数。实验环境为：3.4 GHz Core i3 CPU、16 GB RAM、RedHat Enterprise Linux 7（64 bit）虚拟机（宿主系统为Windows 7），GNU C++编译器。

二元随机CSP的标准模型采用变量个数、值域大小、约束密度和约束紧度四个参数控制实例生成。对于*WS（≠），须增加反映变量值域差异的参数，且互斥约束两端的变量值域即可决定其紧度（违反约束的元组数/该约束值域中所有可能的元组数）。本文通过以下参数控制实例生成：步骤集规模|S|、资源比例μ=|U|/|S|（取资源集规模|U|=|S|×μ）、约束密度ω=2|X|/(|S|×(|S|-1))（以概率ω决定在每一对步骤之间是否生成约束）、每个步骤s的授权比例k=UA(s)/|U|（从U中随机取|U|×k个资源作为s的授权资源集UA(s)）。

实验1现有*WS（≠）算法中，文献[6]（记为C13）具有最低的时间复杂度，文献[10]（记为PB）具有最好的实测时间性能，本实验将与它们进行性能对比，验证算法1的优势。算法1和PB两种回溯算法的实现，均未采用变量排序等额外优化。测试数据模拟较低约束密度下通常规模范围内的工作流，单个实例的生成规则如表1第一行所示。

首先取l=10,u=30，按规则生成400个随机实例，对三种算法的运行时间和峰值空间进行测试。在5 min内，算法1解出了全部实例，PB有1个实例未解出，C13只解出了95个实例。三者在解出实例上的平均时间：算法1为688 μs，PB为1 199 μs，而C13为52 s。C13最多只能求解|S|=17的实例，而算法1和PB均可求解|S|=30的实例。C13在95个解出实例上的最低运行时间为448 ms，而算法1和PB在同样实例上的最大运行时间分别为500 μs和391 μs。尽管C13有最低的时间复杂度，但其实际时间性能与后二者差距很大。一个重要原因是C13基于组合计数而非搜索策略，且空间代价为指数级，仅空间初始化就要相当时间，后二者均为回溯搜索，有机会快速找到一个解。在各自解出实例上的峰值空间：算法1为13.0～13.1 MB，平均13.0 MB，PB始终为12.8 MB，而C13为56.7 MB～14 GB，平均2.9 GB，其最大值已接近测试机物理内存容量。实际上，C13进程在未解出实例上往往运行不足5 min，即因内存分配失败被杀死。根据上述实验，算法1和PB在实测时间和空间性能上远优于C13，而两者之间相对接近，算法1的解出率和平均时间较优，而空间占用略高。

Table 1 Generating rules for test instance表1 测试实例生成规则

进一步取l=31,u=100，按规则生成600个实例，对算法1和PB进行扩展测试。算法1仍然在5 min内解出全部实例，PB的未解出实例为26个。两者在解出实例上的平均时间，算法1为23 ms，PB为406 ms。算法1的解出率和平均时间取得了更大的优势。在共同解出实例上的峰值空间，算法1为13.0～18.9 MB，平均14.3 MB，PB为12.8～13.2 MB，平均12.8 MB。算法1的空间性能仍然略弱于PB。

基于前述1 000个实例的测试结果，图1给出了算法1和PB在973个共同解出实例上的运行时间（μs）对比。图中每个点对应一个实例，其横、纵坐标分别为算法1和PB的运行时间。以x=1 500和y=1 500将该图分为4个象限。在第4象限的实例中，PB均优于算法1，不过最多只快2.9 ms。在第3象限的大部分实例中，PB算法占优，但最多只比算法1快1.1 ms。在第2象限的全部和第1象限的多数实例上，算法 1 优于 PB，比后者快 32 μs～31 s，平均约158 ms，在剩余实例上，PB比算法1快1 μs～83 ms，平均约18 ms。相对于在另外两个象限的劣势，算法1在这两个象限取得了非常显著的优势。对973个实例整体进行统计，算法1的平均时间为13 ms，而PB的平均时间为240 ms，算法1比PB快17倍以上。从分布情况来看，算法1的执行时间集中在较小的区间内，而PB的执行时间更为分散。统计可知，算法1的标准差与平均值之比为1.6，而PB为23.6，算法1围绕均值的平均波动幅度比PB小13倍以上。

综合实验1的结果可知：算法1的解出率、时间和空间性能均远优于C13；算法1较PB有略高的5 min解出率，在解出实例上有13倍以上的平均时间和稳定性优势，其空间性能略弱于后者。

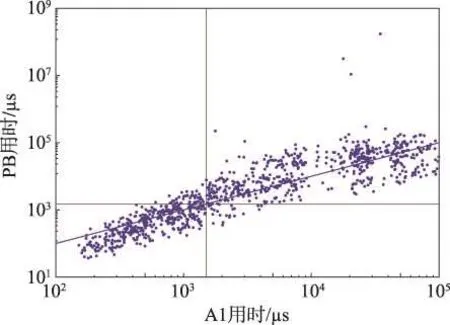
Fig.1 Comparison between runtime ofA1 and PB图1 算法1与PB的执行时间对比

实验2实验1表明了算法1在较低约束密度下的优势，下面进一步考查约束密度增加对其时间性能的影响，即固定|S|和μ，观察算法1执行时间随ω的变化。实例生成规则如表1第二行所示，对每一组|S|.μ.ω，重复生成30个实例，取其中30 min解出实例的平均时间作为测试结果，以消除具体约束分布造成的偶然性。

在生成的4组960个实例上执行算法1，得到如图2所示的4条结果曲线。每条曲线中，运行时间均随约束密度而增加。|S|=200且μ=35的曲线，在ω=75时出现了比较明显的抬升。该点的运行时间约为8 s，是18个重复实例的平均值。该配置集中了960个实例的所有超时情形，有12个实例未在30 min内解出，而其余所有解出实例的最大耗时仅为8 s左右。这就表明，当约束密度大到一定程度时，对于步骤数量很大的实例，算法1的时间性能可能会发生恶化。

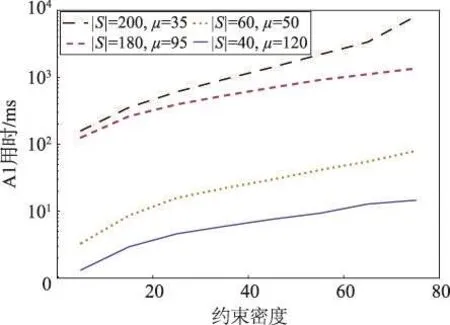
Fig.2 Runtime changes with constraint density图2 运行时间随约束密度的变化

图3给出了上述4组实例树分解宽度W的变化情况，每条曲线的走势与图2中对数纵坐标下对应的曲线大体相仿，两张图中4条曲线之间的差距情况也基本一致。这说明当约束密度ω增加时，算法1时间效率的降低主要是由W增加引起的。进一步观察可知，当ω较小时，图2中每条曲线的增长比较接近甚至慢于图3中对应曲线，而当约束密度较大时，图2中曲线的增长快于图3中对应曲线，甚至末端明显抬升。主要原因是W达到一定大小前，算法可能很快找到一个解，之后由于解空间指数级膨胀，这种机会性急剧降低，使算法效率更接近其理论最坏情形（上述每组实例的资源数均大于10，其最坏情形都是比10W+1更陡峭的曲线），图2曲线的增长速度也随之显现。故约束密度较低时，W的值和算法1的时间复杂度更容易受到控制，而实际性能也更容易利用回溯搜索的机会性取得好的表现。

Fig.3 Tree-decomposition width changes with constraint density图3 树分解宽度随约束密度的变化

5 结束语

本文根据工作流的低约束密度特征，利用树分解回溯技术研究性能平衡的WS（≠）决策算法，从理论上解决了该技术的完备独立分解问题，建立了相应的缓存原理，设计和证明了正确的算法。算法时间复杂度为O*(|S|3×dW+1)，而(W+1)/|S|≤1可取得相当小的值，相对于现有算法时间复杂度均以|S|为指数的情况，一定条件下具有理论优势。实验表明，本文算法有良好的时间性能，明显优于现有实测性能最好和时间复杂度最低的算法。尽管其空间复杂度为指数级，但实测空间性能也有较好表现。