融合多尺度特征的深度哈希图像检索方法*

周书仁，谢 盈+，蔡碧野

1.长沙理工大学 综合交通运输大数据智能处理湖南省重点实验室，长沙 410114

2.长沙理工大学 计算机与通信工程学院，长沙 410114

1 引言

随着互联网中图像数据的日渐增长，如何快速且有效地检索图像这个问题得到了广泛关注。早期基于文本的图像检索技术（text-based image retrieval，TBIR）已不能适应时代的发展，其后出现的基于内容的图像检索技术（content-based image retrieval，CBIR）取得的研究成果显著，其主要针对图像的内容如颜色、形状和纹理等人工视觉特征[1]进行特征提取。

然而，由于图像数据库的规模已然大幅增长，在整个数据库中进行线性搜索需要大量的时间和存储空间，“维数灾难”问题在基于内容的图像检索应用中也时常出现。为了解决这些问题，近年来，近似最近邻搜索（approximate nearest neighbor，ANN）成为了研究热点，哈希算法是最具代表性的方法之一。哈希算法将原始图像映射为一串紧凑的二进制编码，图像之间的相似度可以直接使用汉明距离进行计算，有效地提高了检索效率。因此，基于哈希算法的图像检索技术得到了广泛的研究和应用。

当前主流的哈希算法首先抽取出图像的高维实数特征向量（如颜色、形状等），再通过哈希函数将特征向量转换为一个固定长度的二进制编码（Hash code），则每一幅图像都可以用一串哈希编码来进行表示。与高维实数特征向量相比，哈希编码大幅提高了计算速度，同时减少了检索系统对存储空间的需求。

随着研究的深入，研究者们发现利用基于人工设计的视觉特征进行图像检索时容易产生“语义鸿沟”，而大部分主流哈希算法的性能很大程度上取决于它们第一阶段抽取的特征。因此，提升哈希算法性能的关键之一在于特征提取部分。

目前，由于卷积神经网络[2]（convolutional neural network，CNN）拥有强大的学习能力，研究者们开始将其应用于目标检测、图像分类等计算机视觉任务，取得了突破性的进展。在这些任务中，CNN相当于一个根据特定需求训练得出的特征提取器。其突破性的进展表明：即使在图像外观相差较大的情况下，CNN依然能够有效地捕捉图像的潜在语义信息。

鉴于卷积神经网络在图像处理领域的突出表现，本文提出了一种深度哈希算法，将其用于图像检索以获得更好的性能。该方法的特点包括：（1）将特征学习和哈希学习两部分融合在同一个框架中，实现了端到端的学习；（2）融合多尺度区域信息，构建表达能力更强的特征表示，并减少了网络参数；（3）引入多任务学习机制，结合图像分类信息和图像间的相似度信息学习哈希函数，并且根据信息熵理论，保持哈希编码的均匀分布，提升信息量。

2 相关工作

近年来，近似最近邻搜索的发展十分迅速，而针对高维度海量数据下的最近邻检索问题，哈希算法具有速度快、占用存储空间少等优势，因此备受关注。

早期，研究者们主要对数据独立型哈希算法（data-independent Hashing）进行研究，这类算法的哈希函数通常是随机生成的，独立于任何训练数据，其中最具有代表性的方法是局部敏感哈希算法（locality sensitive Hashing，LSH）[3]。LSH算法利用随机投影生成哈希编码，随着哈希编码位数的增加，二进制编码之间的汉明距离逐渐逼近它们在特征空间中的距离。然而，LSH算法往往需要较长的编码长度才能达到较好的效果，因此这种算法对存储空间的需求较大。

之后，为了克服数据独立型算法的局限性，研究者们提出了数据依赖型哈希算法（data-dependent Hashing），即哈希学习算法（learning to Hash）。这种算法需要从训练集中学习哈希函数，因此不具备通用性，但哈希学习算法可以使得较短的二进制编码所达成的效果也很可观。根据训练数据的不同形式，可以进一步将其分为：有监督哈希算法（supervised Hashing）、半监督哈希算法（semi-supervised Hashing）和无监督哈希算法（unsupervised Hashing）。

无监督哈希算法使用未经过标注的训练数据构造哈希编码，其中包括谱哈希（spectral Hashing，SH）、迭代量化（iterative quantization，ITQ）等经典哈希算法。SH算法[4]最小化图像对之间的加权汉明距离，权值由两两图像间的相似性决定。ITQ算法[5]通过最小化投影后的量化误差来学习哈希函数，从而减少由实值特征空间与汉明空间之间的差异所引起的信息丢失。

有监督哈希算法则充分利用监督信息，如图像的类标签、成对相似度和相关相似度等，来学习紧凑的哈希编码，从而获得相比无监督哈希算法更高的检索精度。CCA-ITQ（iterative quantization-canonical correlation analysis）算法[5]是后续对于ITQ算法的一种延伸，将CCA和标签信息用于降维，然后通过最小化量化误差实现二值化。最小化损失哈希（minimal loss Hashing，MLH）[6]利用基于相似度信息设计的损失函数进行训练。上述方法均采用线性投影作为哈希函数，针对线性不可分的数据则束手无策。为了解决这个问题，KSH（supervised Hashing with kernels）[7]和BRE（binary reconstructive embedding）[8]在核空间（kernel space）中学习保留相似性的哈希函数。

通过分析无监督哈希算法和有监督哈希算法的优势和劣势，研究者们提出了半监督哈希算法SSH（semi-supervised Hashing）[9]。该算法最小化成对标注数据的经验误差并最大化哈希编码的方差。之后，SSTH（semi-supervised tag Hashing）[10]以有监督学习的方式构造哈希编码和类别标签之间的关联，并以无监督学习的方式保留图像之间的相似性。

2010年至2017年，ILSVRC竞赛的历届冠军将图像分类的错误率由28%降低到了2.251%。这期间出现了许多经典的卷积神经网络模型，如AlexNet[2]、VGG[11]、ResNet[12]等。2015年，ResNet解决了网络过深导致的梯度消失问题之后，神经网络的层数得以大幅增加。而在2016年提出的ResNet的变体Res-NeXt[13]证明了增大“基数”比增大模型的宽度或深度效果更好。同年，在保证性能的前提下，DenseNet[14]实现了特征的重复利用，并且降低了存储开销。而近期也有一些研究者聚焦于神经网络的压缩问题[15-16]，期望提高计算速度，减少能源消耗。

随着深度学习的热门，研究者们开始将卷积神经网络与哈希算法相结合进行研究[17-19]，相比人工抽取的特征结合哈希的方法，这种深度哈希方法可以捕捉图像外观剧烈变化下隐藏的语义信息，提升检索精度。2009年，Hinton研究组提出了Semantic Hashing算法[17]。尽管这种算法结合了深度学习和哈希编码，但是深度模型在其中只起到了提供一定的非线性表达能力的作用，网络仍然是由基于人工抽取的特征作为输入，并不算是真正意义上的深度哈希算法。2014年，潘炎研究组提出了CNNH（convolutional neural network Hashing）[18]。这种算法将哈希函数的学习过程分为了两个阶段，第一阶段将成对图像的相似度矩阵分解成基于标签的二进制编码，第二阶段训练卷积神经网络模型拟合第一阶段分解出的二进制编码。2015年，潘炎等人采用NIN网络（network in network）基于三元组排序损失函数进行训练，这种算法被称为NINH（NIN Hashing）[19]，其中提出了divide-and-encode模块用来减少哈希编码的信息冗余。相比CNNH算法而言，NINH算法是端到端的方法，特征学习部分可以与编码部分相互作用。2016年，李武军团队提出了DPSH（deep pairwisesupervised Hashing）算法[20]。该算法基于标签对进行深度哈希学习，并通过减小量化损失提高准确率；同年，DSH（deep supervised Hashing）算法[21]也利用了图像对之间的相似性关系进行模型训练，还衍生出一种在线的图像对生成策略，提高了网络的收敛速度。2017年，王瑞平等人提出的DPH（dual purpose Hashing）算法[22]在训练阶段能同时保留图像类别和图像属性两个层次的相似度；同年，DSDH（deep supervised discrete Hashing）算法[23]将最后一层网络输出直接限制为二值编码以保留哈希编码的离散特性。

通过结合深度学习和哈希编码，上述算法在一定程度上已经改善了检索性能，但仍然存在其局限性。例如，NINH算法采用的三元组排序损失函数对训练样本的选择要求较高，而且其中的divide-andencode模块不够灵活；而DPSH、DSH等算法均只针对图像对之间的相似度来设计损失函数，没有充分利用样本的标签信息。针对这些局限性，本文进一步对深度哈希算法进行了研究：一方面是将图像的标签信息与图像间的相似度信息充分利用以训练网络，且避免了挑选训练样本造成的工作量；而相比divide-and-encode模块，本文的信息熵损失函数既能减少信息冗余，又不受哈希编码长度变化的限制。另一方面，本文针对池化方法进行了改进，构建了表达能力更强的特征表示，并且大幅减少了模型参数，降低了训练过程的计算开销。

3 深度卷积哈希编码

本文提出了一种如图1所示的深度卷积网络架构，用于学习哈希函数。图1分为上下两栏，第一栏是训练网络，第二栏是测试网络。

训练网络主要由三部分组成：（1）由多个卷积层构成的卷积子网络；（2）多尺度融合池化层（multiscale fusion pooling，MSFP）；（3）损失函数部分。训练过程中，网络的输入层要求以图像对的形式输入数据，成对的图像数据经由卷积子网络提取特征，卷积子网络的最后一个卷积层输出若干特征图（feature map）；然后，这些特征图经过多尺度融合池化层融合图像多尺度的区域特征；最终，将区域融合特征送入全连接层（包括隐含层、哈希层和分类层），分别计算分类损失、对比损失和信息熵损失，学习模型参数。

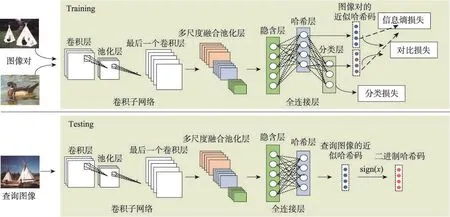
Fig.1 General framework of deep convolutional Hash coding图1 深度卷积哈希编码的总体框架图

测试网络大体上与训练网络一致，只是去除了分类层和损失函数部分。查询图像输入后，由哈希层输出近似哈希码，之后用符号函数将其量化为二进制编码。

3.1 卷积子网络

2015年，何凯明团队提出的深度残差网络ResNet[12]在ILSVCR比赛中表现极佳，该网络模型引入了残差结构（如图2所示），有效地解决了网络太深而引起的梯度消失的问题。

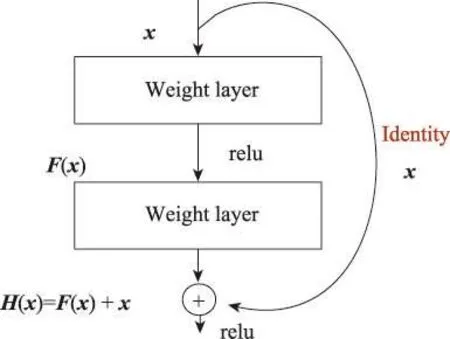
Fig.2 Residual structure图2 残差结构

ResNet不仅训练速度快，计算量小，模型参数少，还显著提升了图像分类的准确率。由于本文的算法思想是要同时利用图像分类信息和图像间的相似度信息进行模型的训练，因此考虑到ResNet在图像分类领域的优越性，本文采用了ResNet-50作为提取图像特征的卷积子网络，训练过程中以图像对作为网络输入，图像对之间共享网络权值。原始的ResNet-50在最后一个卷积层之后连接的是一个全局池化层和一个输出节点数为1 000的全连接层，本文将这两层去除，只保留前面部分作为特征提取器，并在其后增加适应哈希算法需求的其他层（这些在第3.2节和3.3节进行描述）。

3.2 多尺度融合池化

现实生活中，人们向图像检索系统输入的图片尺寸大小不一，而以往的卷积神经网络通常要求输入固定大小的图像，因此图像需要经过裁剪、缩放等操作以统一尺寸，而这些操作往往会造成一定程度的信息丢失。2014年，空间金字塔池化[24]（spatial Pyramid pooling，SPP）被提出来用于解决这个问题。受到SPP池化的启发，本文提出了多尺度融合池化。

如图1所示，本文提出的框架中卷积子网络之后紧跟着的是多尺度融合池化层MSFP，可提取图像不同尺度区域的信息，具体结构如图3所示。

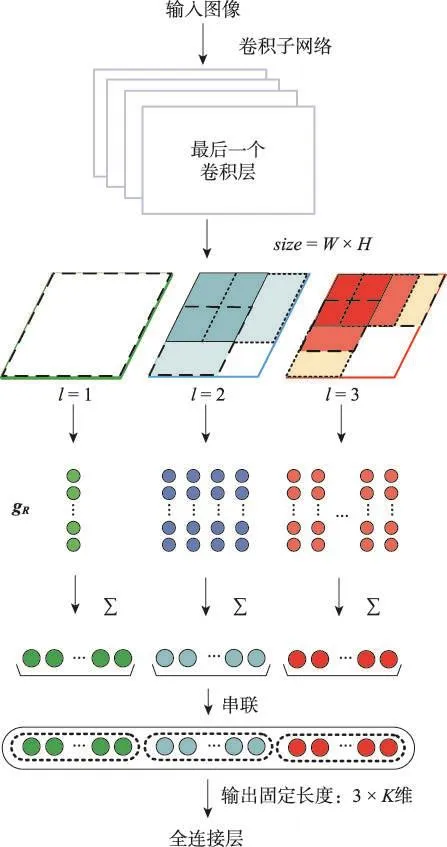
Fig.3 Schematic diagram of multi-scale fusion pooling图3 多尺度融合池化示意图

多尺度融合池化层首先将最后一个卷积层的输出复制为3份，图3中的3个四边形框表示复制的3份卷积层输出。然后，对于每一份卷积层输出，分别按照尺度l=1,2,3均匀划分区域（方形区域的边长由2 min(W,H)/(l+1)决定，图3中采用了不同的虚线框示意划分的区域），在按照不同尺度划分的区域内进行最大池化操作。

假设最后一个卷积层输出K个尺寸为W×H的特征图X={Xi},i=1,2,…,K，某矩形区域R⊆[1,W]×[1,H]的特征向量由式（1）定义：

其中，gR,i=maxp∈RXi(p)，表示在第i个特征通道上区域R的最大值。

如图3所示，在对每个特征图分别进行了不同尺度的最大池化之后，每种尺度会对应产生若干个K维区域特征向量gR，将属于同一尺度的每个区域向量简单相加整合为单列K维特征向量（该过程相当于将同一尺度的所有区域进行了交叉匹配）。最后，将不同尺度的向量串联为一列3×K维的多尺度融合特征向量送入全连接层。

如图4是多尺度融合池化层的一个具体结构示例，图中type表示池化方式，inputs是输入该层特征图的大小，kernel size是不同尺度方形区域的边长（即池化滑动窗口的大小），stride是相邻方形区域间的间隔（即池化滑动窗口的步长）。假设最后一个卷积层输出512个尺寸为7×7的特征图，则在MSFP层按照3种尺度分别进行最大池化得到尺寸为1×1、2×2、3×3的特征图，分别简单相加整合为3列长度为512维的向量，最后串联为一列3×512=1 536维的向量。

Fig.4 Structure example of MSFP图4 MSFP结构示例

卷积神经网络主要由输入层、卷积层、池化层、全连接层和输出层构成。其中，全连接层的输入维度必须是固定的，因此传统的CNN网络通常都要求事先对输入图像进行裁剪、缩放等操作以限制其尺寸，这不可避免地会使得图像在输入网络之前就已损失部分信息，有可能导致提取出的特征不可靠。而本文的多尺度融合池化方法固定输出3×K维向量，在全连接层之前采用MSFP层保证了全连接层的输入维度固定，因此不需要对输入图像的尺寸进行限制，解决了输入图像经过裁剪和缩放后造成的信息丢失问题。

MSFP层划分区域的方式也可以根据需要进行变更，其主要优点在于融合多种尺度的区域信息，输出固定维度的向量，避免了输入图像尺寸的限制，同时相比SPP池化还大幅减少了网络模型参数（SPP池化层输出21×K维向量），有效地降低了计算量，并提高了检索精度（实验部分进行了对比）。

3.3 损失函数

如图5所示，图像i与图像j相似，而其与图像k不相似，它们之间具有相对相似性。为了使图像的二进制编码具有区分度，训练出的卷积网络模型就需要让图像的网络输出能保持这种相对相似性（即减小相似图像(i,j)之间的距离Dji，并拉大不相似图像(i,k)之间的距离Dki）。依据这个原则，研究者通常采用三元组排序损失函数[25]和对比损失函数[21]进行模型的训练。利用三元组排序损失函数训练出的模型性能优劣与否很大程度上取决于三元组样本的选择。假如三元组样本构造不当，在训练阶段会造成极大的干扰，使得网络收敛缓慢。因此考虑到训练阶段的稳定性以及网络的收敛速度，本文采用了对比损失函数[21]训练网络。

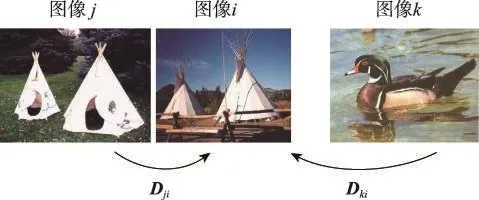
Fig.5 Examples of relative similarity图5 相对相似性示例

假设有N对训练图像(Ii,1,Ii,2)，i=1,2,…,N，这些图像对之间的相似度用yi表示（若相似，yi等于0，否则等于1），则目标函数的构造思路是尽可能地减小相似图像间的距离并加大不相似图像间的距离，即：

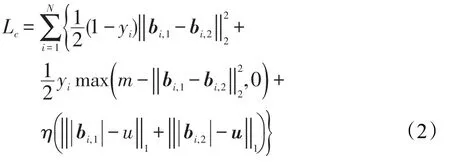
式（2）中，边距参数m>0；bi是图像的近似哈希码；η是量化系数，控制量化误差，使网络输出逼近-1和1；u是一个所有元素均等于1的列向量；‖⋅‖1表示1-范数。为了便于优化，哈希码间的汉明距离采用欧氏距离替代。

根据信息论[26]，任何信息都存在冗余，将其去除冗余后的平均信息量称为信息熵，当信息保持均匀分布时，信息熵达到最大。根据这个理论，信息熵损失函数可以约束网络的输出：

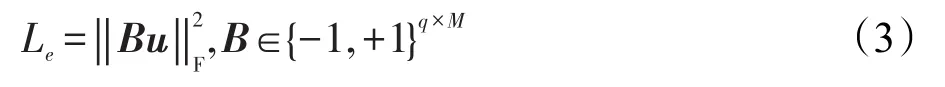
其中，B是全部训练图像的哈希编码所构成的矩阵，本文假设共有M个训练图像，哈希码长度为q。式中的‖⋅‖F表示F-范数。信息熵损失函数在训练过程中会尽可能使得训练数据的二进制编码均匀分布以提升信息量（均匀分布的情况下，第i位哈希码取值为-1的图像数量会和取值为1的图像数量相等）。NINH算法[19]中采用的divide-and-encode模块也可以减少哈希编码的信息冗余，但是模型需要随着哈希码长度的变化进行改动，若是较长的哈希码，所需要分出的子块就会很多，实现过程会较为复杂。相比之下，信息熵损失函数就可以免除这种困扰。

为了充分利用图像的标签信息，本文参考多任务学习机制，还联合了Softmax分类损失函数Ls训练模型参数，使哈希编码能更好地保留语义信息。因此，本文算法的整体损失函数L可以表示为：L=αLs+βLc+λLe，α、β和λ是权重系数。

如图6所示，图像对(Ii,1,Ii,2)经过卷积子网络和多尺度融合池化层提取特征后，图像对的多尺度融合特征向量输入隐含层fc1（节点数为500）和哈希层fc2（节点数等于哈希码长度q），由哈希层输出中间特征向量，然后分为两路：

（1）第一路将图像对的中间特征向量作为近似哈希码(bi,1,bi,2)输入对比损失函数层和信息熵损失函数层。

（2）第二路将图像对的中间特征向量输入分类层fc3（节点数等于图像类别个数），再进入Softmax损失函数层计算分类损失。

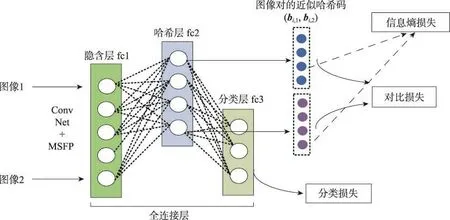
Fig.6 Schematic diagram of loss function part图6 损失函数部分示意图

3.4 哈希编码的生成

如图1中第二栏测试网络所示，网络经过训练之后，给定一幅图像xq输入测试网络，会依次通过卷积子网络、多尺度融合池化层、隐含层以及哈希层，由哈希层fc2输出近似哈希码b(xq)，然后用符号函数计算最终的二值编码：

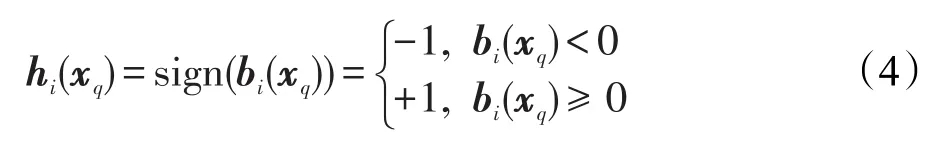
式中，下标i表示哈希编码的第i个元素。

4 实验和分析

4.1 数据集

为了验证文中算法的有效性，本文分别在SVHN、CIFAR-10和NUS-WIDE等数据集上对哈希算法进行了评估。

（1）SVHN

该数据集[27]中的图像超过600 000幅，分为10个类别，每个类别代表一种数字（数字0～9）。本文算法以及其他用于评估的深度哈希算法直接将图像作为输入，其他传统的哈希算法则与文献[21]一样利用GIST特征（维度d=512）表示图像。

（2）CIFAR-10

该数据集[28]包含有60 000张大小为32×32的图片，图片分为10个类别，每个类别有6 000张图片。该数据集与上述SVHN数据集的设置一致，直接将图像作为深度哈希算法的输入，而对于传统哈希算法采用GIST特征输入。

（3）NUS-WIDE

该数据集[29]有269 648张从Flickr收集的图像，属于多标签数据集，每一张图像都与81个语义标签中的一个或者多个相关联。与文献[7]相同，本文只考虑与最常用的21个语义标签相关联的图像，每一个标签至少对应5 000幅图像，最终这个子集共有195 834幅图像。对于深度哈希算法，该数据集的图像直接作为输入，而传统的哈希算法采用官方提供的归一化颜色矩特征（d=225）表示图像[21]。

如图7所示为3个数据集的典型样本示例。SVHN数据集中的图像是由自然场景图像中的门牌号裁剪而来，虽然与MNIST数据集一样是分为0～9这10类数字，但是SVHN中的图像背景复杂，易受光照影响，因此相比之下难度很大。CIFAR-10数据集与SVHN均属于单标签数据集，且图像尺寸均为32×32。但是不同于SVHN中图像全是数字，CIFAR-10数据集的图像是10类不同的物体，如猫、狗、飞机等，数据中含有大量特征，相当有挑战性。而NUS-WIDE数据集中的图像从网络中收集得来，种类丰富且具有多个标签，其复杂的图像信息导致该数据集的检索难度相当大。

Fig.7 Samples of dataset图7 数据集样本示例

本文借鉴文献[21]的数据集划分方式，在数据集CIFAR-10上直接采用官方提供的训练集（50 000幅）和测试集（10 000幅）进行实验；在数据集NUS-WIDE上随机选择10 000幅图像作为测试集，其余的图像作为训练集。而在数据集SVHN中从每一类随机选择100幅图像作为测试集，再从余下的图像中每一类随机选择500幅图像作为训练集。

4.2 实验设置与分析

本文算法基于开源深度学习框架Caffe[30]实现，在训练时权重系数α、β和λ均取值为1，对比损失函数的边距参数m取值为2q，量化系数η则取值为0.01。图像间的相似度yi由图像的标签信息决定：SVHN和CIFAR-10中的图像若是标签一致则视为相似，不一致则视为不相似；而NUS-WIDE中的图像关联多个标签，若图像间有至少一个标签一致，则认为它们是相似的，否则视为不相似。

本文算法与一些主流的哈希算法进行了性能比较：LSH[3]、ITQ[5]、KSH[7]、CNNH[18]、DSH[21]、DLBHC（deep learning of binary Hash codes）[31]。其中，为了快速且公平地评估本文算法，所有基于CNN的算法（CNNH、DSH、DLBHC）均采用了DSH算法[21]的网络结构进行实验评估。之后，使用此结构的本文算法（即该结构最后一个卷积层之后替换为MSFP和3个全连接层以及损失函数层）用Simple-Ours表示，以ResNet-50作为卷积子网络的本文算法用Res-Ours表示。

评估标准采用了MAP（mean average precision）和PR曲线（precision-recall curve）。

表1和表2分别是在数据集SVHN和CIFAR-10上基于本文所提算法与其他主流算法计算出的不同长度编码的MAP值。总体来说，基于卷积神经网络的哈希算法表现优于传统的基于人工抽取特征的哈希算法。从中可以看出，使用相同的网络架构，本文算法（即Simple-Ours）相比其他深度哈希算法，检索精度已得以提升。为了更好地利用图像分类信息，本文基于分类效果极佳的ResNet-50进行了实验，表中Res-Ours的检索精度明显进一步得到了提升。

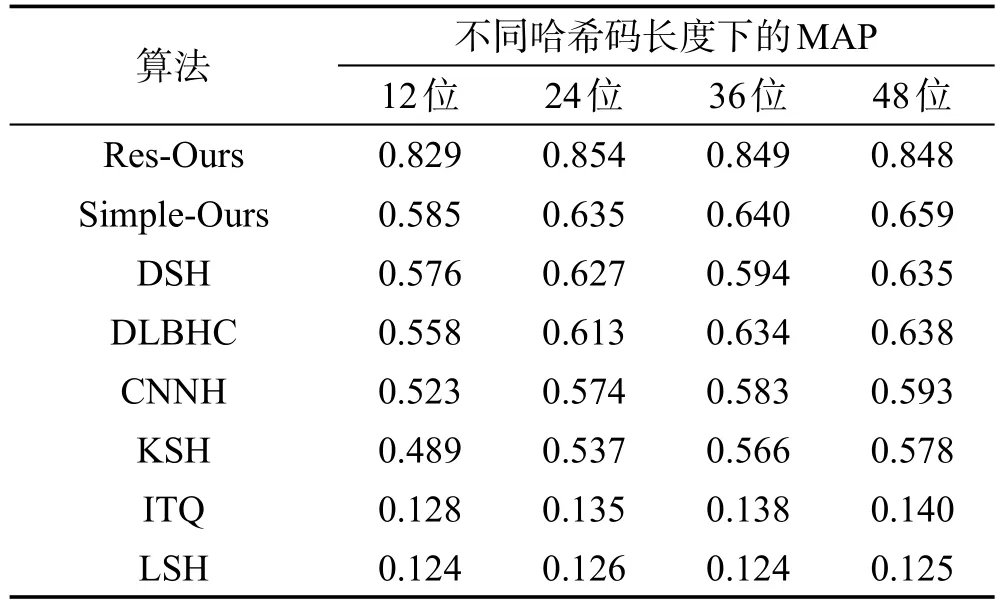
Table 1 MAP of Hash codes with different lengths on SVHN by Hamming sorting表1 在SVHN上不同长度哈希码的汉明排序MAP

表3是在数据集NUS-WIDE上的实验结果，在该数据集上深度哈希算法依然总体优于传统的哈希算法，其中CNNH算法表现略差，是由于该算法同之后的深度哈希算法不同，不属于端到端的学习，其哈希编码的过程与卷积神经网络的训练过程是相互独立的，因此这两个阶段不能互相作用，也就没有发挥出深度网络的强大学习能力。而DSH算法和DLBHC算法没有充分利用图像的标签信息，也没有考虑到哈希编码的信息冗余问题，因此检索精度低于本文算法（Simple-Ours）。本文算法Res-Ours尽可能多地利用了图像分类信息，结合相似度信息，改善了检索性能。

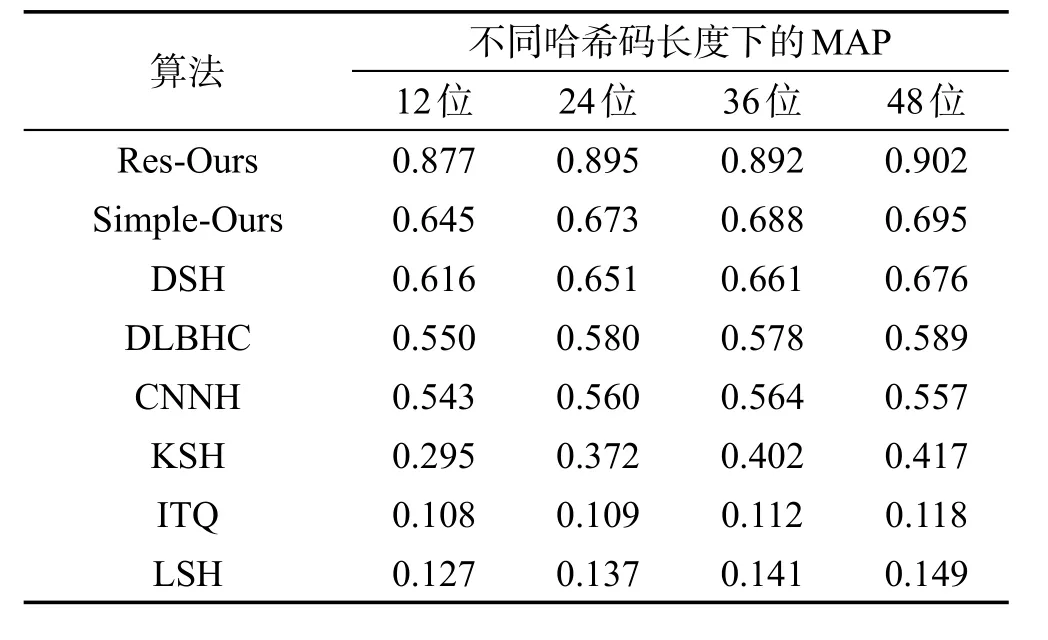
Table 2 MAP of Hash codes with different lengths on CIFAR-10 by Hamming sorting表2 在CIFAR-10上不同长度哈希码的汉明排序MAP

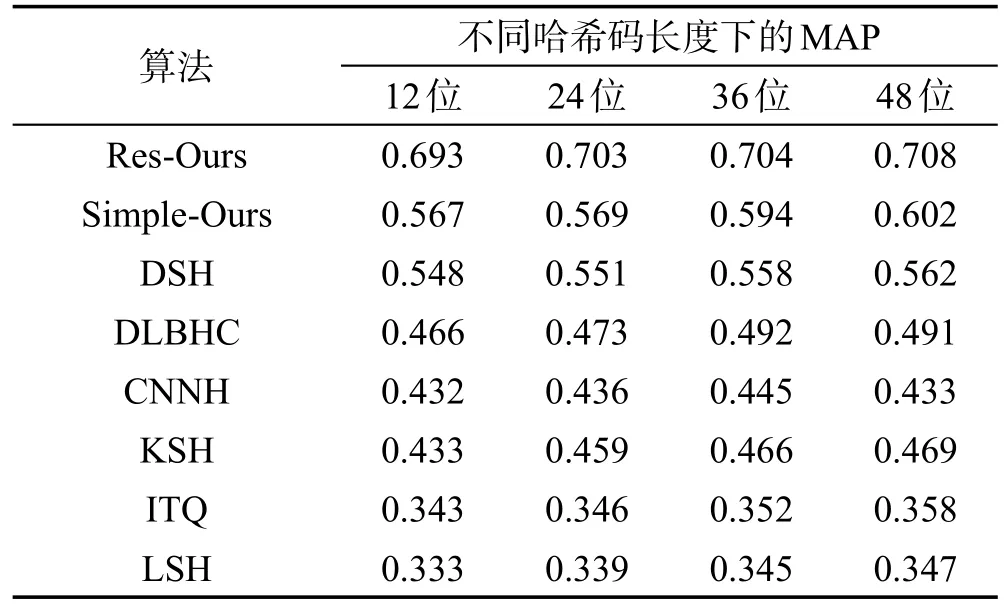
Table 3 MAP of Hash codes with different lengths on NUS-WIDE by Hamming sorting表3 在NUS-WIDE上不同长度哈希码的汉明排序MAP

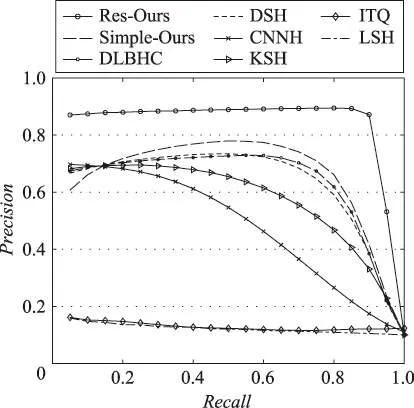
Fig.8 PR curve at 48 bit encoding on SVHN图8 在SVHN上48位编码时的PR曲线

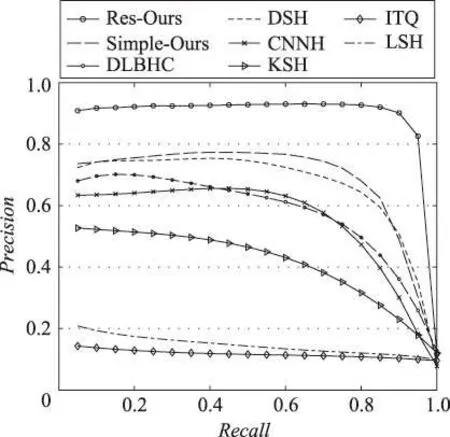
Fig.9 PR curve at 48 bit encoding on CIFAR-10图9 在CIFAR-10上48位编码时的PR曲线

如图8至图10所示是3个数据集上48位哈希码时的PR曲线。从图中可以看出，本文算法在该评估标准下依然具有其优越性。本文实验选取的对比算法都具有代表性，可由实验数据分析得出：（1）有监督哈希算法相比于无监督哈希算法和数据独立型哈希算法更有优势；（2）基于人工抽取特征的哈希算法由于其特征提取过程不够灵活，无法自主学习表达能力强的图像特征，因此总体不如深度哈希算法有效；（3）文中所提算法由于考虑到图像分类信息和图像间的相似度信息可以共同作用于网络训练，并结合了信息熵理论和多尺度融合池化方法，使得检索性能相比当前的深度哈希算法得到了进一步改善。

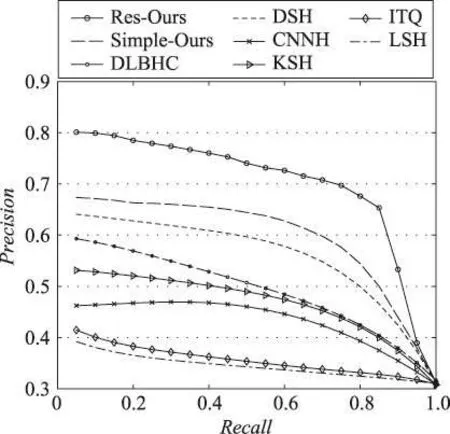
Fig.10 PR curve at 48 bit encoding on NUS-WIDE图10 在NUS-WIDE上48位编码时的PR曲线

4.3 对比MSFP池化与SPP池化

为了证明本文提出的多尺度融合池化MSFP的有效性，在SVHN、CIFAR-10和NUS-WIDE数据集上将其与SPP池化进行了对比（均采用ResNet-50作为卷积子网络，除了最后一个池化层，其他网络结构和设置一致，如图1所示）。表4～表6所示是实验对比的结果。由于NUS-WIDE数据集规模较大，为了减少耗时，采用了检索返回的前5 000幅图像作为整个结果计算MAP，这种评估标准常被使用[19]，记作MAP@top5k。

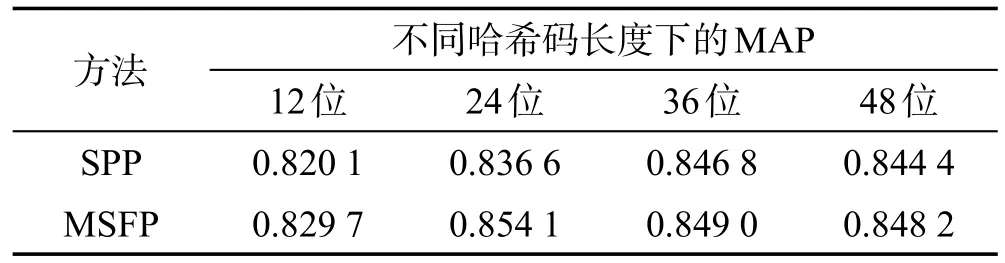
Table 4 MAP contrast of different pooling methods on SVHN表4 在SVHN上不同池化方法的MAP对比

从表4～表6的数据可以看出，MSFP池化在3个数据集上的检索性能与SPP池化相差无几，甚至略有提升。而从表7可以看出，基于MSFP池化训练得到的模型相比基于SPP池化训练得到的模型，由于参数减少，占用空间减小了约70 MB。

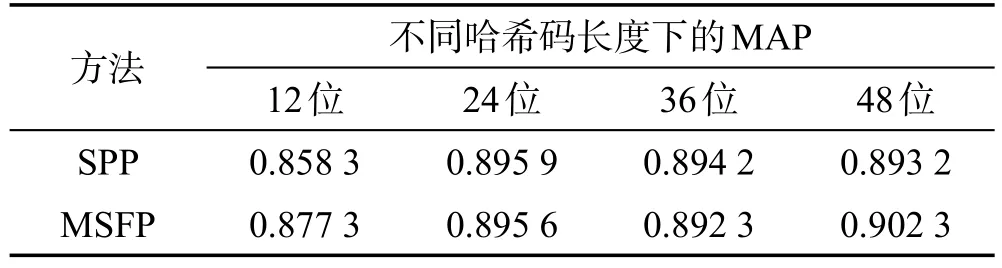
Table 5 MAP contrast of different pooling methods on CIFAR-10表5 在CIFAR-10上不同池化方法的MAP对比

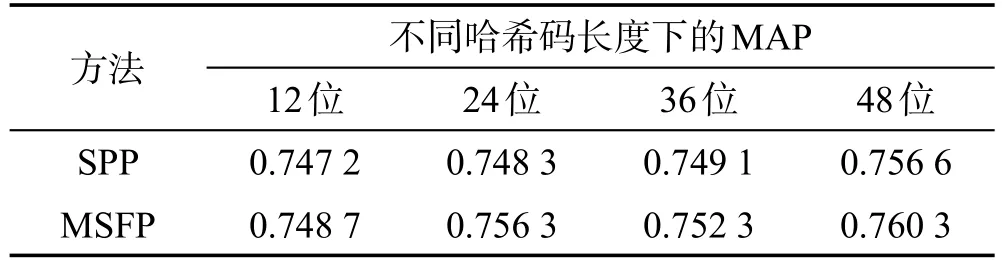
Table 6 MAP@top5k contrast of different pooling methods on NUS-WIDE表6 在NUS-WIDE上不同池化方法的MAP@top5k对比

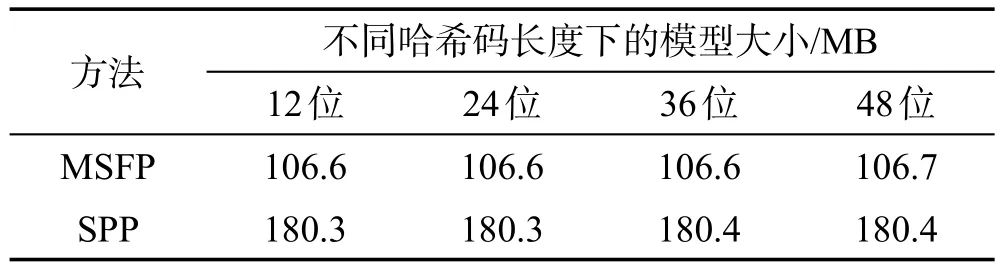
Table 7 Comparison of MSFP and SPP model sizes表7 训练出的MSFP和SPP模型大小对比

经过对两种池化方法的比较分析得出：SPP池化和MSFP池化都是基于多尺度思想提取区域特征，但SPP池化直接将不同尺度的特征串联起来，而MSFP池化先将同一尺度的特征融合，再进行不同尺度特征之间的串联。与SPP池化相比，本文提出的MSFP池化明显减少了模型参数，降低了训练过程的计算开销，但同时也保持了相应的检索精度。

5 结束语

本文提出了一种新的深度哈希算法，基于深度残差网络的强大学习能力，结合多种监督信息训练网络模型，并提出了多尺度融合池化方法。与主流的哈希算法相比，本文算法在实验中实现了最佳的检索性能。此外，本文提出的多尺度融合池化方法不仅提升了检索性能，还减少了模型参数，节省了模型占用空间。