改进的教与学优化算法求解集合联盟背包问题*

吴聪聪，贺毅朝，赵建立,2

1.河北地质大学 信息工程学院，石家庄 050031

2.全北国立大学 电子信息工程学院，韩国 全州 54896

1 引言

集合联盟背包问题（set-union knapsack problem，SUKP）是经典0-1背包问题的一种扩展[1-3]，属于NP完全问题。它在投资决策[2,4]、柔性制造机器[1,5-6]、智慧城市[7]和流压缩[8]等方面都得到了广泛应用。然而，Goldschmidt等人[1]使用动态规划法求解SUKP问题，由于时间复杂度太高而缺乏实用性[3]，Arulselvan提出的基于贪心策略的近似算法[2]，当问题规模较大时也难以在可接受的时间内获得较好解。近期贺毅朝等人[3]提出用演化算法求解SUKP问题的新方法，并提出一种对SUKP问题中不可行解修复和优化的策略——S-GROA（greedy repairing and optimization algorithm）。将该策略分别与二进制蜂群算法、遗传算法和二进制差分演化算法结合，求解三类SUKP问题。从求解速度、精度和稳定性等方面说明进化算法是解决SUKP问题的可行实用的方法。

教与学优化算法[9]（teaching-learning-based optimization，TLBO）是由Rao等人在2011年提出的一种新的进化算法。由于TLBO具有参数少、结构简单、求解速度快等特点，已经引起很多国内外学者的关注[10-20]，并在机械设计与处理的问题优化[11]、热交换优化处理[12]、热冷器优化[13]、平面钢框架设计[14]、数据聚类分组[15]经济调度问题[16]等领域得到良好应用。

然而，TLBO算法本身也存在着对于较复杂问题寻优精度低，稳定性差，收敛速度不够快的不足[17]。为此，国内外学者在TLBO算法的改进和优化上进行了广泛的研究。Rao等人[17]在原算法基础上加入了精英策略，提出了ETLBO算法（elitistTLBO，ETLBO），ETLBO算法比原始算法在收敛速度和求解精度方面都有所提高。Rajasekhar等人[18]提出了相对精英教学优化算法（elitist teaching learning opposition based algorithm，ETLOBA），该算法在寻优精度及收敛速度上比ETLBO算法有所增强。于坤杰等人[19]提出了基于反馈的精英教与学优化算法（feedback ETLBO，FETLBO），该算法在学生“学”阶段之后加入“反馈”阶段，使算法在寻优精度上取得了较好的效果。王培崇等人[20]通过引入混沌优化、学生动态自适应学习、精英个体的共轭梯度搜索、反向学习和高斯学习，对TLBO进行了四方面的改进，提高了算法的收敛精度。但是以上改进算法，文献[17-19]策略较简单，改进后的算法在性能上还有提升空间；文献[20]中共轭梯度搜索不好确定迭代次数，而且对算法搜索全局最优解的作用不稳定。因此，针对TLBO的特点和所求解问题，恰当地选择优化措施非常重要。

本文针对求解SUKP问题，提出一种改进的二进制教与学优化算法（modified binaryTLBO，MBTLBO）。首先将TLBO算法通过编码转化机制设计成能求解SUKP问题的二进制TLBO算法（BTLBO）。然后，针对SUKP问题，提出改进的贪心优化策略MS-GROA（modified S-GROA），该策略通过对可行解的二次优化，能够进一步提升解的被优化程度，从而提高SUKP的求解精度。另外，从教与学算法角度，在算法的“教”阶段和“学”阶段引入差分演化算法的交叉算子，让进化得到的临时个体与原个体进行交叉操作，平衡算法的全局搜索和局部开发能力，避免算法早熟；通过在精英个体周围，以自适应标准差，按正态分布进行局部搜索，进一步提高算法的求解精度和收敛速度。最后，进行了3组（每组10个实例）SUKP实例仿真。实验结果表明，MBTLOB算法与已有的求解SUKP问题的进化算法（二进制蜂群算法、遗传算法和二进制差分演化）相比，平均求解精度更高，改进的修复和优化策略MS-GROA比原策略在对解的优化上更有效。

2 SUKP定义

定义1给定元素集合U={u1,u2,…,un}和项集S={U1,U2,…,Um}，项集S中的每项Ui(i=1,2,…,m)是元素集合U的子集，即Ui⊆U，且每个项Ui拥有一个价值pi>0。U中的每个元素uj有一个重量wj>0(j=1,2,…,n)。将项集S中的项装入载重为C的背包，如果设装入背包的项构成的集合为A，那么A的价值P(A)是A中所有项的价值之和，A的重量W(A)是A中所有项并集中包含的元素重量之和。要解决的问题就是：如何选择S中的项装入背包，使得装入集合A的重量W(A)在不超过载重C的情况下价值P(A)最大？上面的问题可以用下面的数学模型描述[1-2]：

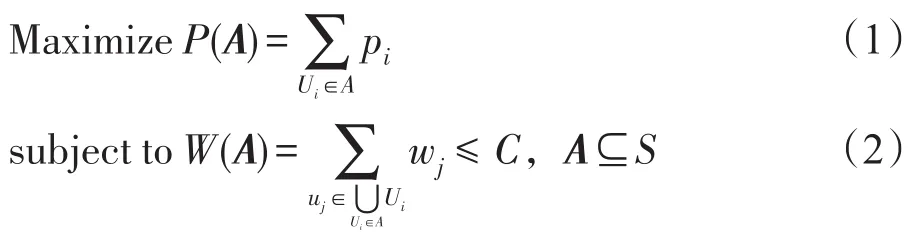
为了便于使用启发式算法解决SUKP问题，文献[3]给出了一种整形规划的数学模型，模型如式（3）和式（4）：

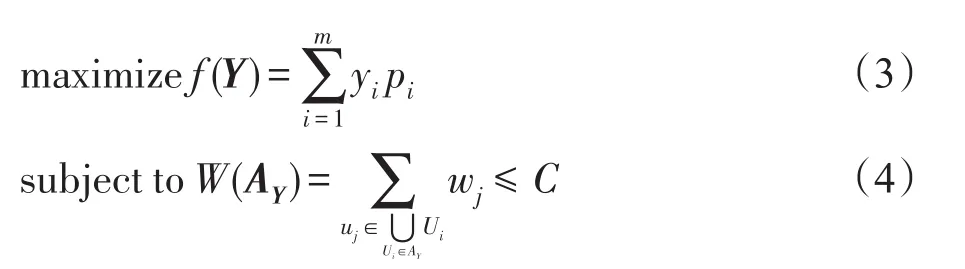
其中，Y={y1,y2,…,ym}∈{0,1}m是m维的0-1向量，当yi=1(i=1,2,…,m)时表示集合S中的第i项Ui属于集合AY，当yi=0(i=1,2,…,m)时表示集合S中的第i项Ui不属于AY，AY是装入背包的项构成的集合，即AY⊆S。

3 二进制教与学优化算法

3.1 教与学优化算法

教与学优化算法（TLBO）是根据课堂教学中教师和学生的行为提出的一种群优化算法。TLBO算法分为“教”和“学”两个阶段：“教”阶段学生跟随教师学习，“学”阶段是学生之间相互学习。算法中的教师由学生中成绩最好者（适应度最高的个体）来担任，学生数量为种群规模N，学生个体为实向量Xi=[xi,1,xi,2,…,xi,m]，i=1,2,…,N，教师用实向量Tt=[t1,t2,…,tm]表示。

3.1.1 “教”阶段

在“教”阶段，每个学生根据班级平均状态与教师状态的差异进行学习。用差异向量D表示班级平均状态与教师状态的差异，该向量由式（5）计算得到，然后再由式（6）求得当前个体学习后的新个体Xnewi，如果新个体Xnewi的适应度更高，则由新个体代替原个体，否则原个体保持不变。

式（5）中，rt是[0,1]上的随机数，Tt为教师个体，Mt为全班平均状态（即），λ为教学因子，它决定平均值改变的程度，其值可以是1或2，由式（7）计算得到。

式（7）中，round表示四舍五入取整函数，rand(0,1)产生0到1之间的随机数。

在“教”阶段，实现的是群体中的个体向最优个体不断靠拢的过程。

3.1.2 “学”阶段

在此阶段，学生相互学习。任意一个学生个体Xi(i=1,2,…,N)，随机选择其他两个不同的学生个体Xk1、Xk2，如果Xk1的适应度高于Xk2的适应度，按式（8）学习；否则，按式（9）学习。如果学习产生的新个体Xnewi的适应度更优，则Xnewi代替Xi，否则，Xi不变。

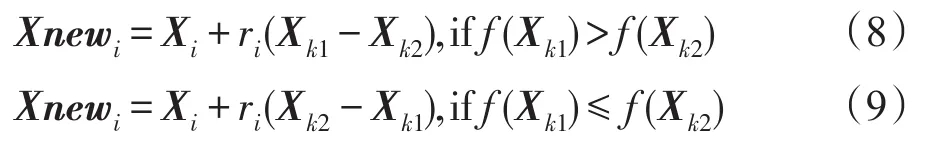
式（8）和式（9）中，ri是每个个体学习的随机系数，是在[0,1]上的随机数。

“学”阶段相当于对个体的变异，实现全局搜索。

3.2 二进制教与学优化算法

教与学优化（TLBO）算法是基于求解连续函数的优化问题而提出的，本文使用编码转换方法[21-26]，将其设计成能求解组合优化问题的二进制TLBO算法（binary TLBO）。令每个学生个体或临时个体用一个二元组(X,Y)表示。实向量X=[x1,x2,…,xm]，xj∈[1,-1]，j=1,2,…,m，有一个与之对应的二进制向量Y=[y1,y2,…,ym]，yj∈{0,1}，j=1,2,…,m，二进制向量利用从连续空间[-1,1]d到离散空间{0,1}d的映射得到，映射关系为式（10）所示。算法中个体的进化针对个体的实数向量X进行，二进制向量Y按式（10）随之产生，个体的适应度由二进制向量Y计算得到。

4 改进的二进制教与学优化算法求解SUKP问题

4.1 改进的贪心修复策略MS-GROA

因为SUKP问题是一个约束组合优化问题，在用进化算法求解SUKP过程中对不可行解的处理是不可避免的。文献[3]在文献[2]的贪心策略基础上提出一种贪心优化算法S-GROA，和几种进化算法结合求解SUKP实例取得了很好的效果。本文在S-GROA基础上加入了二次优化，使得其对解的优化性能更强。

S-GROA首先要计算S中每个项的价值密度，然后按价值密度由高到低的次序对项目进行装入处理。针对SUKP的特点，当候选解（也叫潜在解，解的可行性不知，一般是进化中的个体向量）经过S-GROA算法的处理后虽然已经是较优化的可行解，但还有再优化的可能。对于S中没有装入的项Uk，如果Uk中所包含的元素已经都在Az中，即满足{uj|uj∈Uk}⊂，那么Uk的加入不会增加装入项的总重量，即W(Az)=W(Az∪{Uk})，而使Az总价值增加，即P(Az)=P(Az)+pk。将符合该条件的Uk项装入，会使Az总价值增加而总重不变，将得到更优化的可行解。由此本文设计了改进的贪心修复优化算法MSGROA（modified S-GROA）。

令dj(j=1,2,…,n)是集合U中每个元素在子集U1,U2,…,Um(Ui∈S)中的使用频率，令(i=1,2,…,m)，设S中的每一项的价值密度为pi/Ri。使用快速排序按价值密度的降序对S中的各项进行排序，将排序后各项序号存入数组H，对于一个二进制向量Z=[z1,z2,…,zm]∈{0,1}m，令AZ={i|zi∈Z且zi=1,1≤i≤m},zi=1表示S中项Ui加入背包中。目标函数fsukp(Y)（也是适应度函数）的值按式（3）计算，在此基础上算法MS-GROA描述如下。

算法1MS-GROA

输入：SUKP潜在解Y=[y1,y2,…,ym]∈{0,1}m和数组H[1…m]。

输出：可行解Y=[y1,y2,…,ym]∈{0,1}m和该解的目标函数值fsukp(Y)。

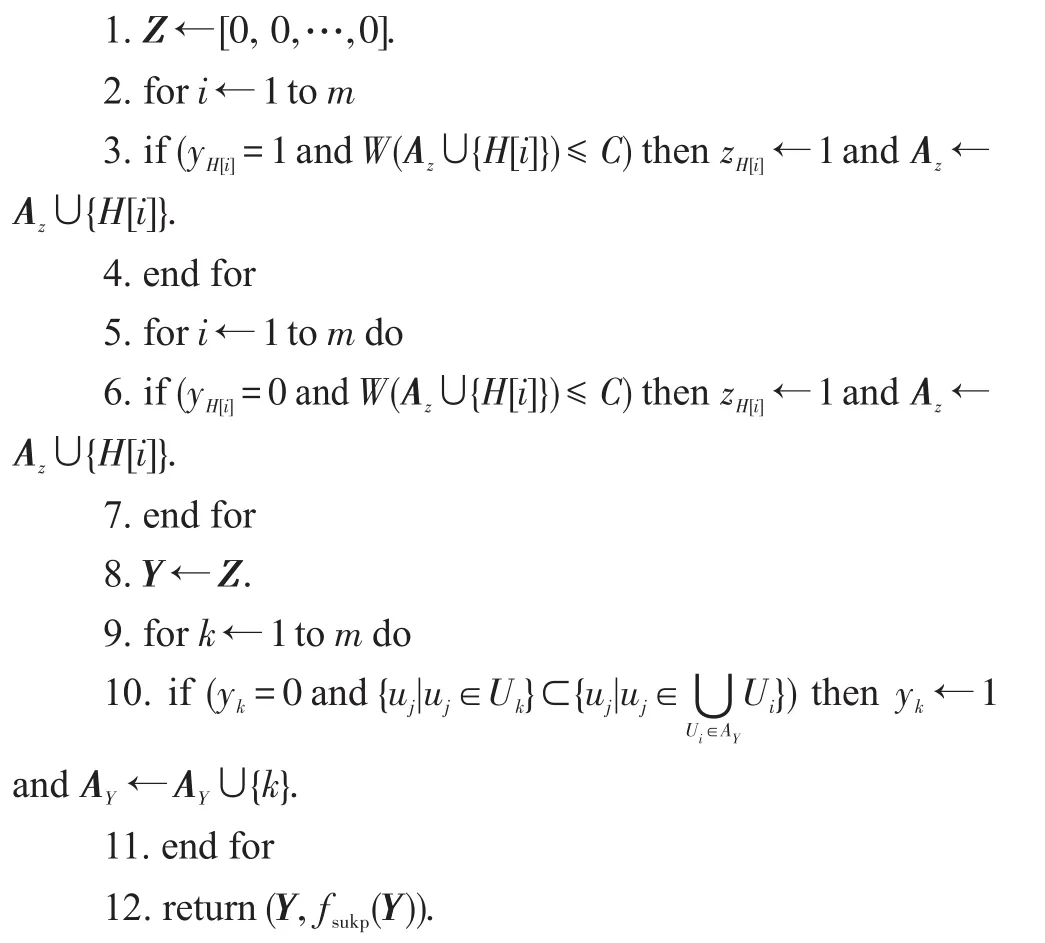
和σfinal分别是标准差的最初值和最终值，经过多次测试，本文设置为σinitial=1，σfinal=0.3；n为非线性调和因子，一般情况下[32]ψ=3。分析得到：随着进化，按式（12）产生的标准差是从较大标准差变化到较小标准差，使得在算法进化前期，此局部搜索在精英个体周围以比较松散的形式进行，正符合实际情况的需要，算法进化前期，精英个体距离全局最优解一般比较远，这种松散搜索可以提高找到最优解的机率；而到后来的标准差较小，实现了在精英个体较近处的细微搜索，此时精英个体一般离全局最优解很近，细微搜索更容易找到全局最优。

以上两个策略分别从群体中的普通个体和精英个体两个角度对算法进行了优化，考虑到普通个体和精英个体在群进化中所起作用的不同，对他们分别采用了不同的策略。两种策略同时实施于教与学优化算法，可以有效平衡算法的局部开发和全局勘探的能力。加入两个策略的BTLBO算法称为MBTLBO算法（modified BTLBO），该算法比BTLBO具有更强的寻优能力和收敛速度，通过后面的仿真实验也得以证明。

4.3 改进的二进制教与学优化算法求解SUKP问题

在使用MBTLBO求解SUKP问题时，每个学生个体(Xi,Yi)的二进制向量就是SUKP问题的候选解，用MS-GROA算法对每代所得候选解进行修复和优化，同时得到个体的适应度。下面给出求解SUKP问题的MBTLBO算法。

首先使用快速排序QuickSort算法对上文提到的S中各项按价值密度pi/Ri(i=1,2,…,m)从大到小排序，并将排序后的序号存入数组H[1…m]中。此过程描述为H[1…m]←QuickSort(S)。算法2给出了用MBTLBO求解SUKP问题的伪代码。

算法2MBTLBO for SUKP

输入：SUKP实例数据，最大迭代次数Maxiter，种群规模N。

输出：算法求出的近似解（或最优解）Bt和目标函数值fsukp(Bt)。

分析求解SUKP问题的MBTLBO算法的时间复杂度：首先计算pi/Ri(i=1,2,…,m)的时间复杂度为O(mn)；快速排序H[1…m]←QuickSort(S)的时间复杂度是O(mlbm)；对个体潜在解修复优化并计算适应度(Yi,fsukp(Yi))←MS-GROA(Yi,H)的时间复杂度O(mn)；在MBTLBO算法中，步骤1～4时间复杂度为O(mn+mlbm+Nm)，步骤5～33时间复杂度为Maxiter×O(Nmn)，而这里最大迭代次数Maxiter和种群规模N均为小于等于max{m,n}的数，如令Q=max{m,n}，则MBTLBO算法的时间度为O(Q4)，是多项式时间求解SUKP问题的进化算法。

5 仿真实验和分析

仿真实验使用文献[3]提供的3组SUKP实例，每组由10个测试实例构成。3组SUKP实例运行结果如表1～表3所示。这3组实例分类是按S中的项目个数m和U中的元素数n的关系来确定的。第1组实例中m>n，第2组实例中m=n，第3组实例中m＜n。每个实例用一个m×n的0-1矩阵M表示项目集S={U1,U2,…,Um}，对应M中的每个元素rij，只有当元素uj∈Ui时，才有rij=1。实例的名字以sukpm_n_α_β为统一的样式，其中m是实例中的项目数，n是元素个数，α表示在矩阵M中1出现的密度，，β是背包载重C与所有元素重量之和的比率，。

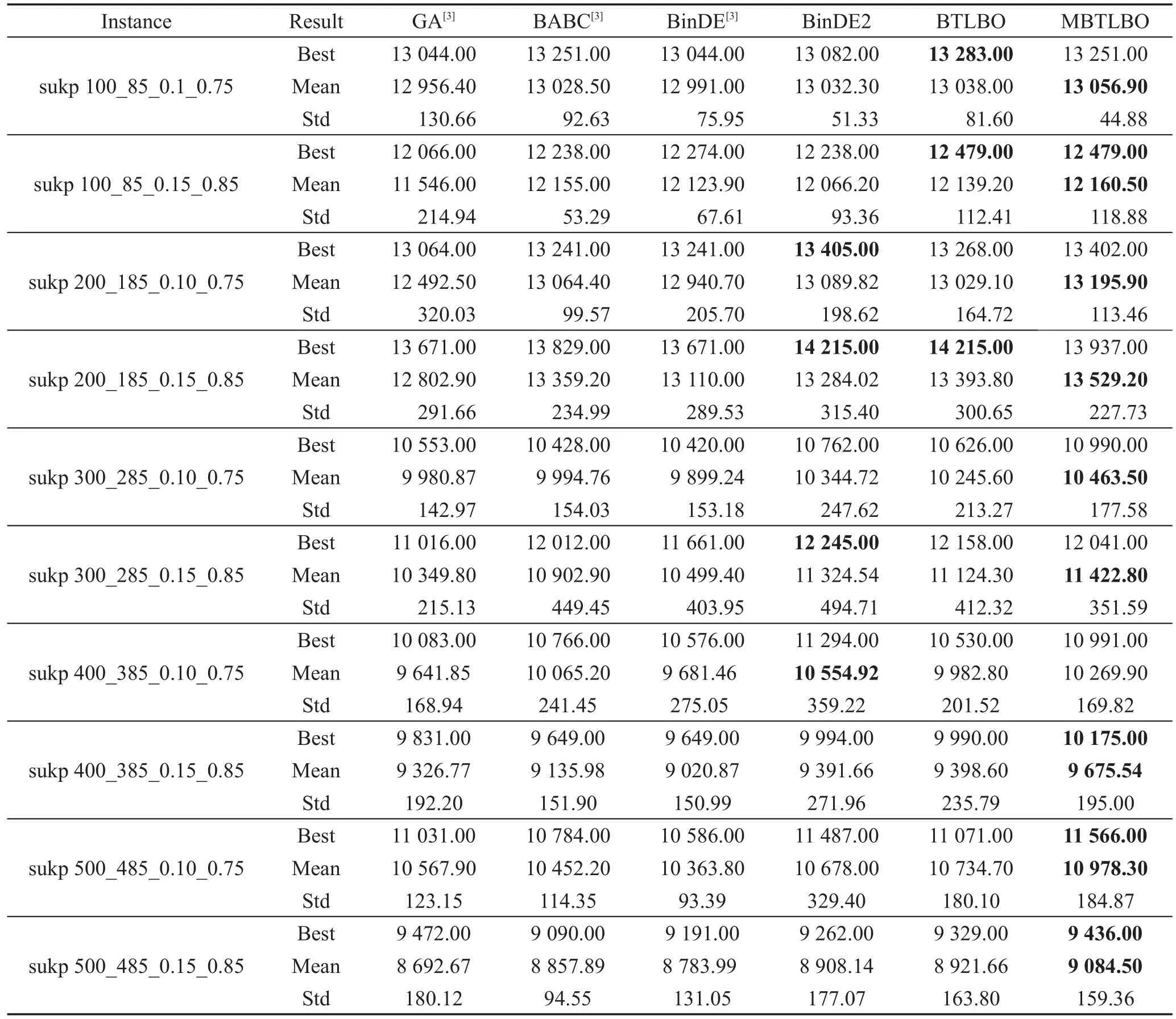
Table 1 Computing results of the first kind of SUKP instances表1 第1组SUKP实例测试结果

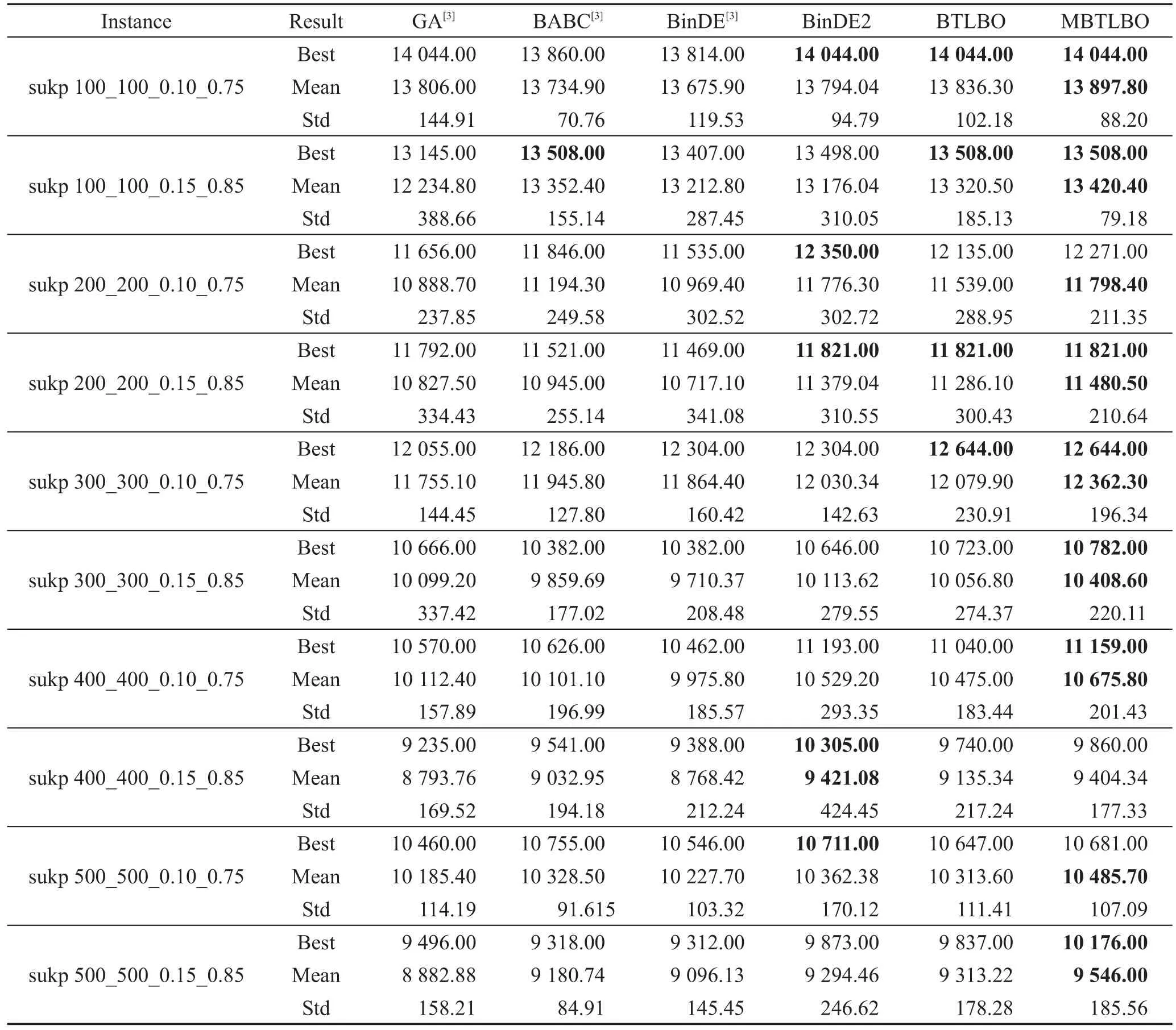
Table 2 Computing results of the second kind of SUKP instances表2 第2组SUKP实例测试结果

实验在配置为Intel®Core™i5-7Y54 CPU@1.2 GHz，内存8 GB的电脑上进行，操作系统为Windows 10，编程环境VC++2010，所有代码由C++编写。

为了测试新算法的性能，将本文提出的MBTLBO算法与文献[3]中求解SUKP问题的较好算法（包括遗传算法GA（genetic algorithm）、二进制蜂群算法BABC（binary artificial bee colony）、二进制差分演化算法BinDE）以及BTLBO进行比较。为测试本文对贪心修复策略改进的效果，将二进制差分演化算法BinDE[33]与本文的MS-GROA算法结合求解SUKP，与文献[3]中使用S-GROA求解SUKP的二进制差分演化算法BinDE算法进行比较。为便于区分，将本文的二进制差分演化算法命名为BinDE2。

BinDE2参数设置与文献[3]中BinDE相同；MBTLBO算法中交叉因子Cr=0.8,σinitial=1和σfinal=0.3,ψ=3。所有实例独立运行50次，最大迭代次数设置和文献[3]相同，即Maxiter=max{m,n}。表 1～表 3 中Best、Mean、Std是50次运行实例所得结果的最优值、均值和标准差。表中粗体表示所有实验结果中的最好值。

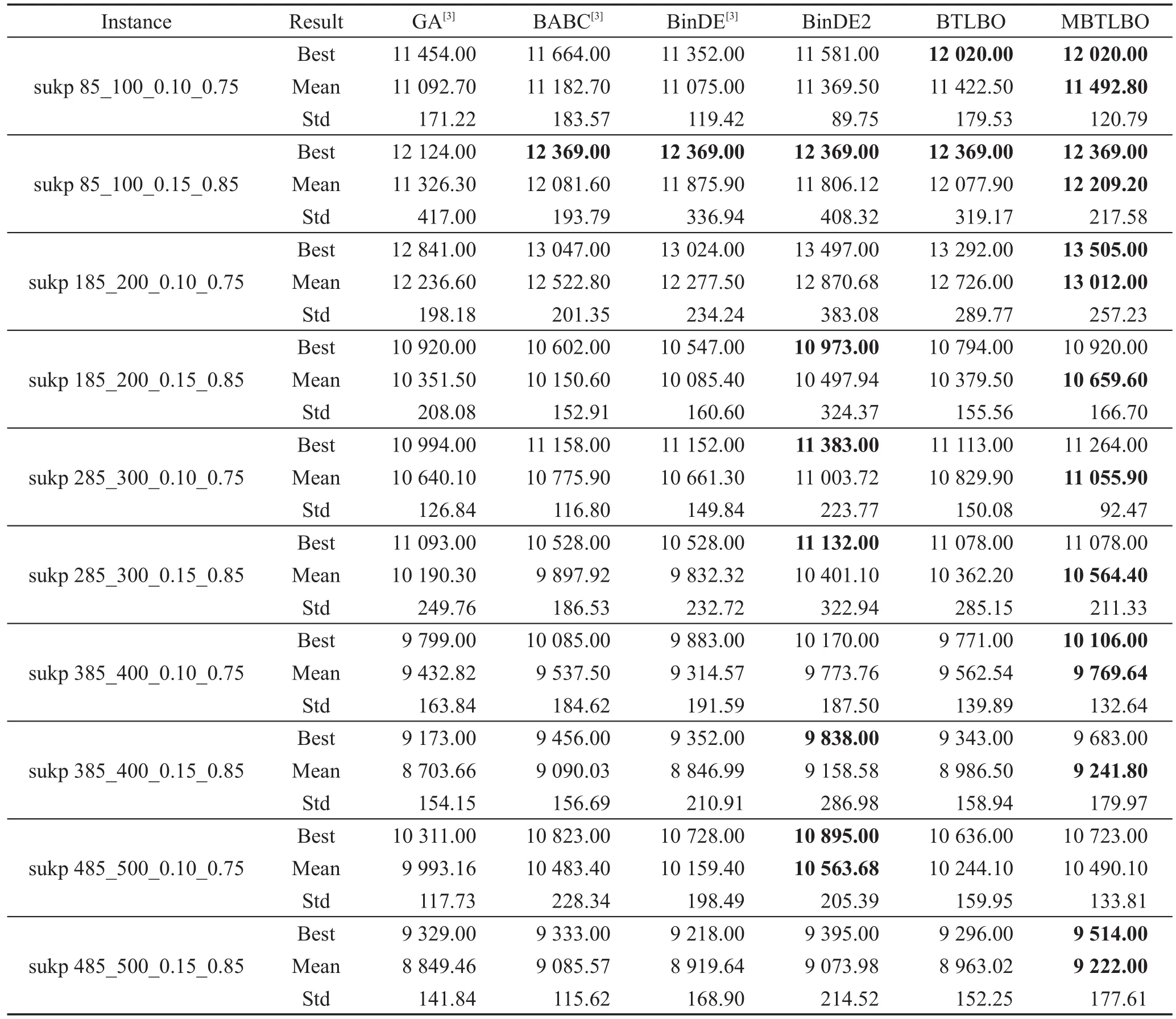
Table 3 Computing results of the third kind of SUKP instances表3 第3组SUKP实例测试结果

从表1～表3可以看出，六种算法中，MBTLBO、BinDE2和BTLBO三种算法，在修复和优化候选解时使用本文提出的MS-GROA策略，其他三种算法使用了文献[3]的S-GROA策略，由于MS-GROA中加入了对可行解的二次优化，尽最大可能性将项目放入背包，进一步提高了解的精度，使得在30个实例的求解中，MBTLBO、BinDE2和BTLBO求解性能排在前三位，均超过其余三种算法。从BinDE和BinDE2的实验数据比较中也明显看出MS-GROA的作用。在三组实例中，BinDE2在27个实例上求得的最优值高于BinDE，在29个实例上求得的均值高于BinDE2。而两种算法都是使用BinDE[33]算法在相同参数配置下求解SUKP问题，不同之处是，文献[3]使用S-GROA对候选解进行修复优化，本文使用MS-GROA。由此可见，MS-GROA策略是一种比S-GROA更有效的对SUKP候选解修复和优化的策略。

另外，在三种求解较好的算法中，MBTLBO求解的效果明显好于其他两种算法，是求解能力最强的算法。MBTLBO与BinDE2相比：MBTLBO有17个实例的最优值高于BinDE2，有27个实例的均值高于BinDE2。MBTLBO与BTLBO相比：MBTLBO有19个实例求得的最优值好于BTLBO，有30实例求解的均值都高于BTLBO，有23个实例的标准差好于BTLBO。由此说明，MS-GROA策略的使用提高了进化算法求解SUKP问题的性能，而同样使用MSGROA策略的三种进化算法MBTLBO、BinDE2和BTLBO中，MBTLBO由于对普通个体引入了差分算法中的交叉算子，并实施了精英局部搜索策略，提高了算法的求解精度，增强了算法求解的稳定性。

为更直观地反映交叉算子和自适应精英局部搜索策略对二进制教与学算法的优化作用，图1～图3给出了二进制教与学算法BTLBO和改进的二进制教与学算法MBTLBO求SUKP实例的平均收敛曲线图，由于篇幅有限，只给出了每组中的四个实例的收敛曲线图。

从这12个平均收敛曲线图明显看出，MBTLBO由于引入了针对普通个体的交叉算子和针对精英个体的自适应搜索，在迭代前期就可以非常明显增加算法的局部搜索能力，使算法的收敛效率得以提高。对普通个体的交叉操作，使得整个种群均匀地提高了算法向各个个体周围的开发能力，增强了跳出局部极值的可能性，从而使MBTLBO的收敛稳定性得到了加强。而对精英个体的自适应局部搜索，随着迭代次数的增加，搜索的宽度由大到小，在算法中前期也起到了跳出局部优值的作用，同时提高了算法的寻优精度，使MBTLBO始终保持高于BTLBO的精度和收敛趋势。由此可见，本文提出的MBTLBO确实加快了算法的收敛速度，提高了算法获取全局最优解的概率，算法的寻优性能得到了改善。

综上所述，本文提出的改进二进制教与学优化算法（MBTLBO）是求解SUKP问题的有效算法。MS-GROA策略是一种更有效修复和优化SUKP解的方法。

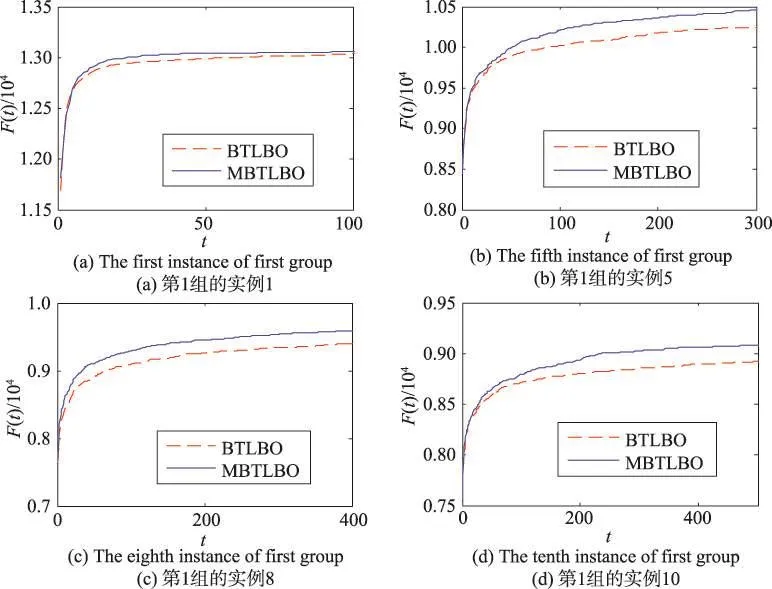
Fig.1 Average convergence plot for 4 instances of the first kind of SUKP using MBTLBO and BTLBO图1 MBTLBO和BTLBO在第1组中四个实例的平均收敛曲线图

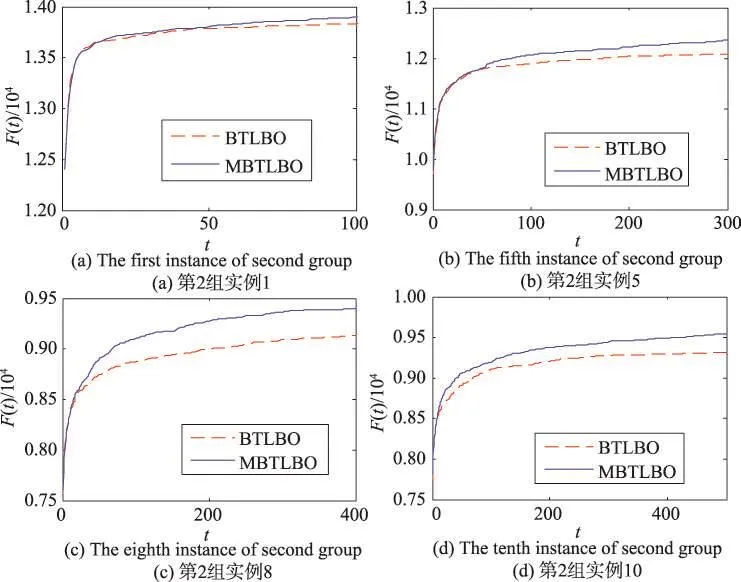
Fig.2 Average convergence plot for 4 instances of the second kind of SUKP using MBTLBO and BTLBO图2 MBTLBO和BTLBO在第2组中四个实例的平均收敛曲线图

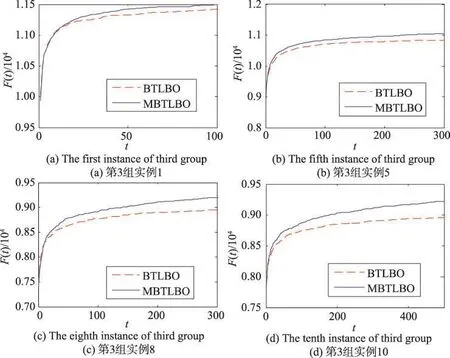
Fig.3 Average convergence plot for 4 instances of the third kind of SUKP using MBTLBO and BTLBO图3 MBTLBO和BTLBO在第3组中四个实例的平均收敛曲线图

6 结束语

本文提出了一种改进的二进制教与学优化算法（MBTLBO）求解SUKP问题。针对SUKP问题本身，提出一种改进的修复优化策略（MS-GROA），MSGROA在原修复优化策略（S-GROA）的基础上增加了对可行解的二次优化，进一步提高了求解精度。MS-GROA是一种通用的方法，可用于求解SUKP问题的其他进化算法中。通过分析基本教与学优化算法和现实中学生学习的行为，对学生的学习做出了改进。在学生学习过程中，引入差分演化算法中的二项式交叉算子，平衡了教与学优化算法进化过程中的全局勘探能力和局部开发能力；借鉴杂草算法中杂草的繁衍方式，在精英个体（教师）周围按正态分布进行自适应搜索，提高了算法的寻优能力和收敛速度。仿真实验表明改进的二进制教与学优化算法是求解SUKP问题的有效方法。