模糊交互时态逻辑的一些标记*

朱 晔，袁红娟,+，钱俊彦，潘海玉

1.泰州学院 计算机科学与技术学院，江苏 泰州 225300

2.桂林电子科技大学 广西可信软件重点实验室，广西 桂林 541004

1 引言

模型检测[1-3]是一种验证安全攸关反应式系统关键性质的自动化技术。其中系统的行为用Kripke结构来描述，而系统的性质则用时态逻辑[1-3]公式来描述，通过遍历Kripke结构的状态空间来验证性质是否成立。用模型检测对具有模糊不确定性信息的系统进行验证，即称为模糊模型检测。模糊模型检测是经典模型检测理论的延伸和推广。近年来，模糊模型检测引起了学术界和工业界的广泛关注，并取得了较大的发展。

模糊模型检测技术首先由加拿大学者Chechik等人[4]于2003年提出。他们研究了基于De Morgan代数的计算树逻辑的模型检测问题并设计出模型检测工具[5]。以色列学者Shoham和Grumberg[6]探讨了具有相同代数结构的μ-演算的模型检测问题。最近，基于抽象和精化思想，Meller、Shoham、Grumberg[7]解决了有限De Morgan代数的μ-演算的组合模型检测问题[8]。我国学者在模糊模型检测问题的研究方面做了很多工作。李永明等人[9-11]结合模糊理论中的可能性测度及模型检测技术，提出广义可能性模型检测方法。潘海玉等人[12-13]研究了基于任意模糊逻辑的计算树逻辑的模型检测问题及取值于任意有限格的计算树逻辑的模型检测问题。

目前的模糊模型检测技术主要适用于模糊封闭式系统的验证，即模糊系统的行为由系统本身的当前状态决定，与系统的工作环境无关。为了对模糊开放系统使用模糊模型检测技术，即模糊系统的行为不仅受到系统内部状态的制约，同时受到外部环境交互的影响。文献[14]将Rlur等人提出的并发博弈结构CGS（concurrent game structure）和它的规范语言交互时态逻辑ATL[15]（alternating-time temporal logic）推广到模糊情形下，用不动点迭代算法解决所获得的逻辑的模型检测问题。值得一提的是，ATL已经被用于多智能体系统[16]、电子商务业务流[17]，以及概率开放系统[18]等的分析验证。

本文的研究任务是文献[14]工作的延续。首先通过将模糊交互时态逻辑的模型检测问题转化为有限个经典的交互时态逻辑的模型检测问题，从而将模糊交互时态逻辑的模型检测可以转化为使用经典的时态交互逻辑的模型检测算法来解决，进一步分析了模糊交互时态逻辑的模型检测问题的不动点迭代算法的时间复杂性。最后研究了模糊交互时态逻辑语义的连续性问题，即模糊并发博弈结构发生微小变化时，模糊交互时态逻辑的语义是否也相应地发生微小的变化。

与本文工作最相关的是广义可能性计算树逻辑的模型检测问题[9-11]的研究。广义可能性计算树逻辑用可能性算子 GPo（generalized possibility operator）取代计算树逻辑的路径全称量词和路径存在量词。为了解决广义可能性计算树逻辑的模型检测问题，文献[11]利用截集的方法，将广义可能性计算树逻辑的模型检测问题规约为经典的计算树逻辑模型检测，给出了解决广义可能性计算树逻辑的模型检测问题的算法及其计算复杂度。

2 预备知识

本章将回顾模糊并发博弈结构和模糊交互时态逻辑的语法和语义。在正式引入模糊交互时态逻辑的语法和语义之前，给出一些记号。后文用N表示自然数集合，用S+表示有限状态序列集合。设X是经典集合，则函数F:X→[0,1]成为集合X上的模糊集合。若X是有限集合，||X表示集合X中的元素个数。设A和B是X上两个模糊集合，后文用A⊆B表示A(x)≤B(x)，x∈X。

定义1[14]（模糊并发博弈结构）模糊并发博弈结构（fuzzy concurrent game structure，FCGS）是六元组：

M=(n,S,AP,V,d,δ)其中：

（1）n是系统中智能体的数目，用自然数1,2,…,n来指代每个智能体，用Σ表示智能体集合{1,2,…,n}。

（2）S是有限状态集。

（3）AP是有限原子命题集合。

（4）V:S×AP→[0,1]是模糊赋值函数，状态s∈S，原子命题p∈AP，V(s,p)表示状态s下，满足原子命题p的真值。

（5）da(s)表示系统在状态为s下，智能体a可用的非空动作集合，这里，a∈Σ，s∈S。＜j1,j2,…,jn>表示系统在状态s下，智能体集合Σ可采取的一个动作向量，其中，ja∈da(s)。同时，定义动作向量集D(s)=d1(s)×d2(s)×…×dn(s)。

（6）δ是状态迁移函数，表示系统在动作向量＜j1,j2,…,jn>∈D(s)的作用下，从状态s迁移到下一个状态δ(s,j1,j2,…,jn)。

注意到，经典的并发博弈结构是一种特殊的FCGS，因为若FCGSM的模糊赋值函数的值域限制为{0,1}，则M为经典的并发博弈结构。若没有特别说明，后文用M表示一个FCGS。

智能体a的策略fa是一个函数fa:S+→Ν：如果λ的最后状态为s，则fa(λ)∈da(s)。{fa|a∈A}为A的联盟策略，记作FA。另外，记ΠA为A的所有的联盟策略之集。令FA∈ΠA。用out(s,FA)表示联盟体A遵循联盟策略FA得到的所有源自s的路径集合。换句话说，若λ=s0s1s2…∈out(s,FA)当且仅当s0=s，且对于任意i≥ 0，存在动作向量 ＜j1,j2,…,jn>∈D(si)，使得任意a∈A，ja=fa(λ(0,i))，δ(si,j1,j2,…,jn)=si+1。这里用λ(i)，λ(0,i)，λ(i,∞)分别表示状态路径λ的第i个状态、λ的有限前缀和λ的无限后缀。

下面给出用于描述FCGS性质的模糊交互时态逻辑的语法和语义。

定义2[14]（FATL语法）原子命题集合AP上的模糊交互时态逻辑（fuzzy alternating-time temporal logic，FATL）公式定义如下：

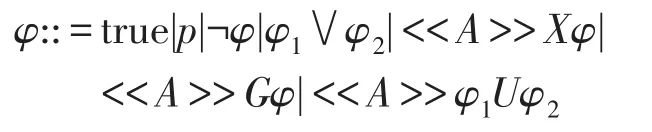
其中，p∈AP，A⊆Σ。

定义3（FATL语义）设φ为FATL公式，M=(n,S,AP,V,d,δ)是FCGS，φ在M上的语义定义如下：对于任意状态s，有

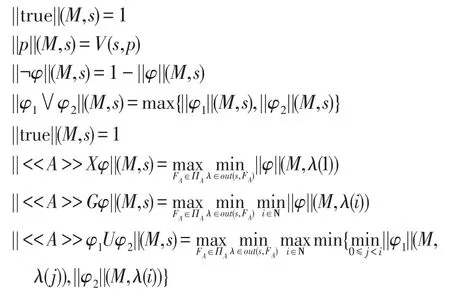
从上述定义不难看出，FATL的语法和经典ATL的语法是完全一致的，它们的区别主要表现在其语义上。

值得一提的是，若定义3中的语义模型FCGS就是经典的并发博弈结构，那么FATL的语义与ATL的语义是一致的。若M是经典的并发博弈结构，常用M,s╞φ表示||φ||(M,s)=1。当上下文明确时，常省略M。

命题1[14]设M=(n,S,AP,V,d,δ)是FCGS。φ1、φ2、φ为FATL公式，Y是S上的一个模糊集合，函数E、F分别定义如下：

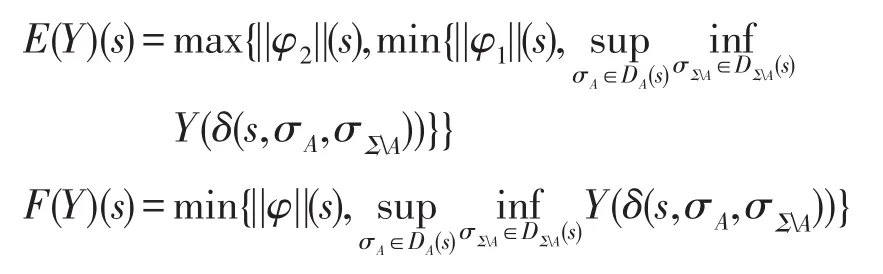
其中，s∈S。则 ||＜＜A>>φ1Uφ2||和||＜＜A>>Gφ||分别是E(Y)和F(Y)的最小和最大不动点。

3 模型检测

本章通过将FATL的模型检测问题转换为有限个ATL的模型检测问题，进而可利用ATL的模型检测法来解决FATL的模型检测问题。FATL的模型检测问题是指：对于给定的FCGSM，状态s∈S及FATL公式φ，计算||φ||(s)的值。在正式讨论FATL的模型检测问题之前，引入一些记号。

设φ是FATL公式，公式φ的长度，记作|φ|，归纳定义为：

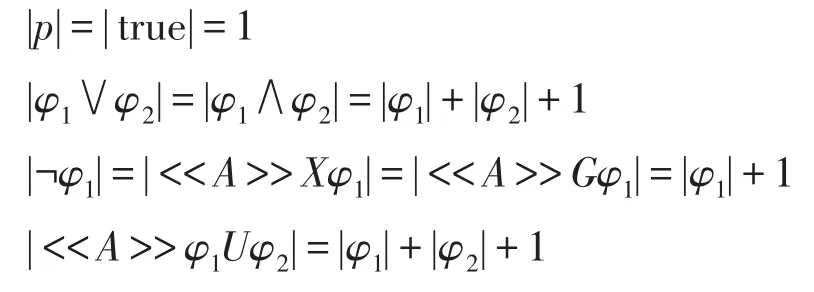
模型FCGSM的规模大小为：

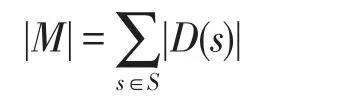
定义4（阈值为α的并发博弈结构）设M=(n,S,AP,V,d,δ)是一个FCGS，对任意的α∈[0,1]，构造一个并发博弈结构Mα为：

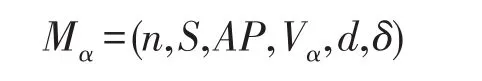
其中，Vα(s)={p:V(s,p)≥α,p∈AP}。

引理1设φ是不包含¬连接词的任意FATL公式，M是一个FCGS，则对任意的α∈[0,1]以及M中的任意状态s，||φ||(M,s)≥α当且仅当Mα,s╞φ。

证明采用结构归纳法证明。

（1）当φ=true时，||true||(M,s)=1≥α⇔Mα,s╞true。

（2）当φ=p，p∈AP时，由Mα的定义知，||p||(M,s)≥α⇔Mα,s╞p。

（3）当φ=φ1∨φ2时，由归纳假设知：

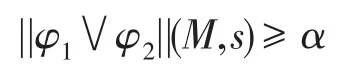
（4）当φ=＜＜A>>Xφ1时，由归纳假设知：

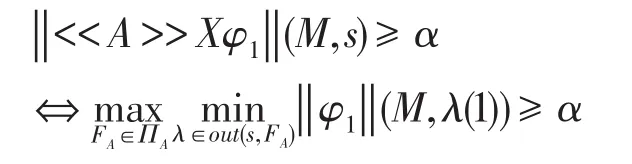
⇔在M中存在一个策略FA∈ΠA，对于任意的λ∈out(s,FA)，有 ||φ1||(λ(1))≥α

⇔在Mα中存在一个策略FA∈ΠA，对于任意的λ∈out(s,FA)，有Mα,λ(1)╞φ1

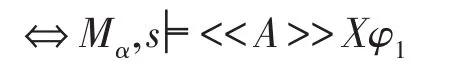
（5）当φ=＜＜A>>φ1Uφ2时，由归纳假设，定义3和定义4知：

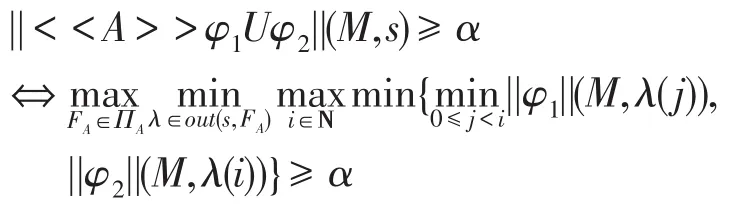
⇔在M中存在一个策略FA∈ΠA，对于任意的λ∈out(s,FA)，存在一个i∈N 使得||φ2||(λ(i))≥α且对于任意的j,0 ≤j＜i，||φ1||(λ(j))≥α

⇔在Mα中存在一个策略FA∈ΠA，对于任意的λ∈out(s,FA)，存在一个i∈N使得Mα,λ(i)╞φ2且对于任意的j,0≤j＜i，

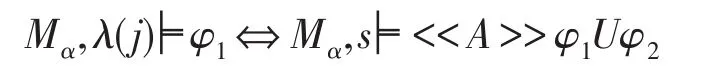
（6）当φ=＜＜A>>Gφ1时，由归纳假设，定义3和定义4知：

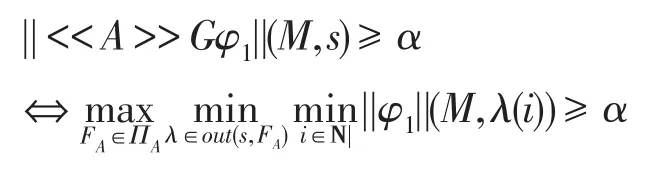
⇔在M中存在一个策略FA∈ΠA，对于任意的λ∈out(s,FA)和i∈N，||φ1||(M,λ(i))≥α

⇔在Mα中存在一个策略FA∈ΠA，对于任意的λ∈out(s,FA)和i∈N，Mα,λ(i)╞φ1

根据以上结论，下面定理1的证明过程给出了将FATL的模型检测问题转换为经典的ATL的模型检测的方法。

定理1（时间复杂度）设φ是任意的FATL公式，M是一个FCGS，则对任意状态s，计算||φ||(s)的时间复杂度是O(|φ|·|M|·|S|·|AP|)。

证明若φ=¬φ1，根据定义2，可先通过计算||φ1||(s)，然后求 ||φ||(s)=1-||φ1||(s)。由引理 1 知，若φ不包含¬连接词的FATL公式，则对任意状态s有||φ||(s)=max{α∈Im(M):Mα,s╞φ}，这里Im(M)={V(s,p):s∈S,p∈AP}⋃{1-V(s,p):s∈S,p∈AP}。因此 FATL 的模型检测问题可转换为至多|Im(M)|个ATL的模型检测问题。注意到经典的ATL的模型检测问题能在O(|φ|×|M|)时间内解决。因此计算||φ||(s)的时间复杂度是O(|φ|× |M|× |S|× |AP|)。

通过下面的例子解释如何将FATL的模型检测问题规约为ATL的模型检测问题，并利用定理2中的算法步骤求 ||φ||(s)。

例1现在用一个模糊并发博弈结构FCGSM=(n,S,AP,V,d,δ)来建模市场中两家企业销售某产品的情况，其中：

（1）n=2表示有两家企业：企业1和企业2。

（2）S={s0,s1,s2}，s0表示市场供小于求，s1表示市场供求平衡，而s2表示市场供大于求。

（3）AP={a,b}，表示企业1销售该产品方式：高价垄断a和薄利多销b。

（4）V(s0,a)=0.6，V(s1,a)=0.3，V(s1,b)=0.4，V(s2,b)=0.5，V(s2,a)=V(s0,b)=0表示产品在不同市场状态下不同销售方式成功的可能性，例如V(s0,a)=0.6表示供不应求的市场状态下，高价垄断方式销售成功的可能性是0.6。

（5）d1(s0)=d1(s1)=d1(s2)={1,2}，d2(s0)=d2(s1)=d2(s2)={1,2}表示各企业在各市场状态下采取的不同动作来进行销售，提高利润。其中，d1(s0)={1,2}，表示供小于求的市场状态下，企业1增加市场产品投放量（动作1）和提高产品科技含量（动作2）。d2(s0)={1,2}，表示供小于求的市场状态下，企业2采用提价（动作1）和维持原价（动作2）。d1(s1)={1,2}，表示供求平衡的市场状态下，企业1采用保持原价及赠送礼包（动作1）和提高科技含量（动作2）。d2(s1)={1,2}，表示供求平衡的市场状态下，企业2采用降价（动作1）和维持原价（动作2）。d1(s2)={1,2}，表示供大于求的市场状态下，企业1采用赠送礼包促销（动作1）和降价处理（动作2）。d2(s2)={1,2}，表示供大于求的市场状态下，企业2采用降价处理（动作1）和提高产品科技含量（动作2）。

（6）δ(s0,1,1)=δ(s0,1,2)=s1，δ(s0,2,1)=δ(s0,2,2)=s0，δ(s1,1,1)=δ(s1,1,2)=s2，δ(s1,2,1)=δ(s1,2,2)=s0，δ(s2,1,1)=δ(s2,2,1)=s2，δ(s2,1,2)=δ(s2,2,2)=s1。表示不同市场状态下，在企业间的联合动作下，市场状态变迁情况。

该结构如图1所示。

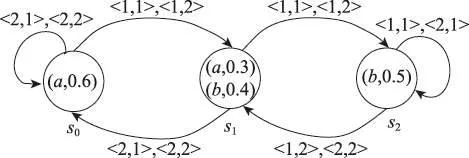
Fig.1 Schematic diagram of FCGS图1 FCGS示例图

设φ=＜＜1>>aUb。用定理1的证明过程中提出的模型检测方法来计算||φ||。首先令α=0.3，构造出M0.3=(n,S,AP,V0.3,d,δ)，其中：

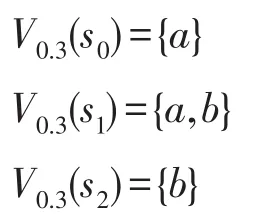
根据ATL的模型检测算法，得到：

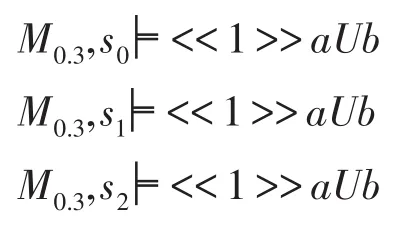
再令α=0.4。同理可以构造出并发博弈结构M0.4=(n,S,AP,V0.4,d,δ)，其中：

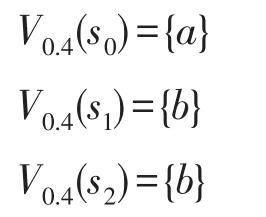
也利用ATL模型检测算法，得到：

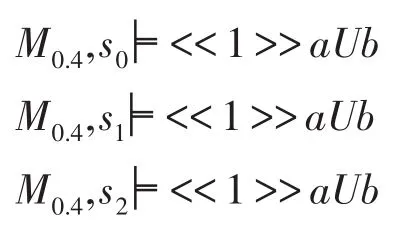
然后令α=0.5。则构造出并发博弈结构M0.5=(n,S,AP,V0.5,d,δ)，其中：

最后令α=0.6。则构造出并发博弈结构M0.6=(n,S,AP,V0.6,d,δ)，其中：

因此

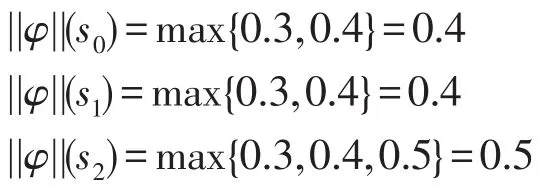
文献[14]指出采用不动点迭代算法FATL公式φ的模型检测问题需要O(|φ|×|M|×|S|×|AP|)时间。根据定理1，给出不动点迭代算法的时间复杂性一个更理想的渐进上界。

定理2设φ是任意的FATL公式，M是一个FCGS，则采用不动点迭代算法能在复杂度为O(|φ|×|M|×|S|)时间内正确地计算 ||φ||的值。

证明用φ=＜＜A>>Gφ1为例来说明本定理成立。根据已有结论，对任意状态s，Mα,s╞＜＜A>>Gφ1当且仅当在Mα中存在一个策略FA∈ΠA，对于任意的λ∈out(s,FA)和i≤|S|，Mα,λ(i)╞φ1。因此由定理1可得这 说明用不动点迭代算法求解||＜＜A>>Gφ1||至多需要|S|次迭代，而每次迭代需要O(|M|)时间，因此采用不动点迭代算法能在复杂度为O(|φ|×|M|×|S|)时间内计算出 ||φ||(M,s)。

4 一致连续性

本章研究FATL语义的一致连续性。为了研究FATL语义的一致连续性，需要给出FCGS间“距离”的概念。

定义5（距离）给定两个FCGSM1=(n1,S1,AP1,V1,d1,δ1)和M2=(n2,S2,AP2,V2,d2,δ2)且满足n1=n2,S1=S2,AP1=AP2,d1=d2,δ1=δ2，M1和M2间的距离定义为：

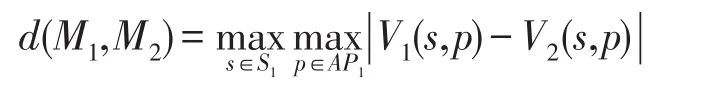
定理3设φ是FATL公式。对于任意给定的ε>0，存在一个η>0，使得只要d(M1,M2)＜η，有|||φ||(M1,,这里S是FCGSM1和M2的状态集合。

证明利用结构归纳法证明定理成立。

（1）当φ=true时，结论明显成立。

（2）当φ=p，p∈AP时，对于任意的ε>0，令η=ε，当d(M1,M2)＜η时，显然有：

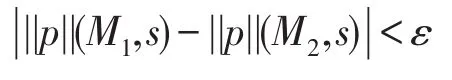
（3）当φ=¬ψ时，由归纳假设知，对于任意的ε>0，存在η>0，当d(M1,M2)＜η时，满足|||ψ||(M1,s)-||ψ||(M2,s)|＜ε。由定义2得到：

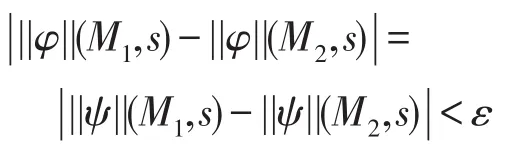
（4）当φ=φ1∨φ2时，根据归纳假设，任意的ε>0，存在η1>0，当d(M1,M2)＜η1时，满足：

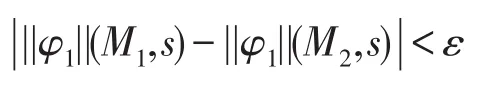
同样地存在η2>0，当d(M1,M2)＜η2时，满足：

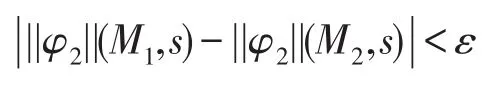
令η=min{η1,η2}，则d(M1,M2)＜η，可以推出：

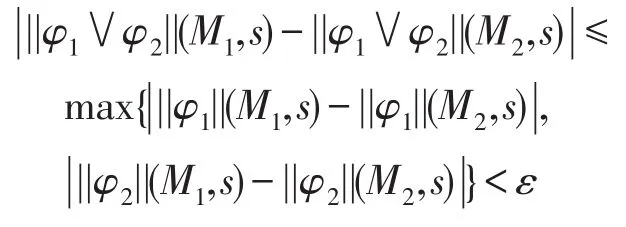
（5）当φ=＜＜A>>Xφ1时，由归纳假设知，对于ε>0，对于任意的FA∈ΠA，λ∈out(s,FA)，存在ηλ>0，当d(M1,M2)＜ηλ时，使得：

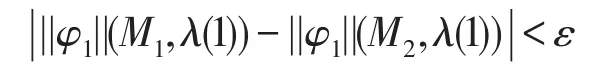
令η=min{ηλ:FA∈ΠA,λ∈out(s,FA)}，由d(M1,M2)＜η可以推出：

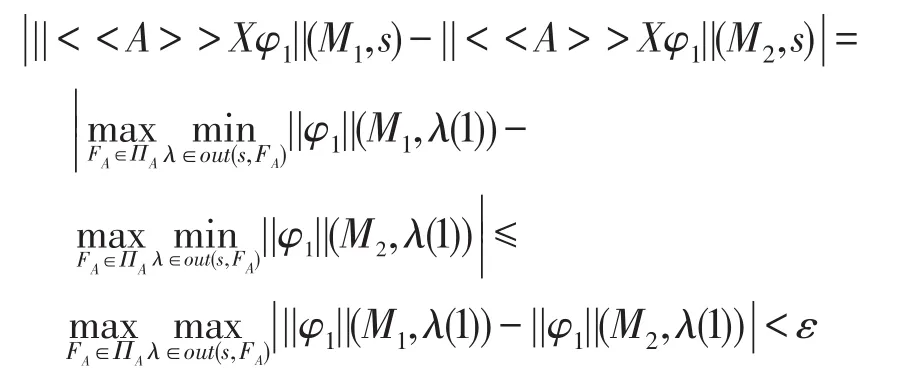
（6）当φ=＜＜A>>φ1Uφ2时，由命题1，序列x0=∅，xn+1=||φ2||(M1)⋃(||φ1||(M1)⋂||＜＜A>>X||(xn))的极限是||＜＜A>>φ1Uφ2||(M1)，序 列y0=∅，yn+1=||φ2||(M2)⋃(||φ1||(M2)⋂||＜＜A>>X||(xn))的极限是 ||＜＜A>>φ1Uφ2||(M2)。对n实施归纳法证明命题对于φ=＜＜A>>φ1Uφ2情形成立。当n=0时，结论明显成立。设n≤k时定理成立。当n=k+1时，由归纳假设对于任意给定的ε>0，存在一个η1>0，使得只要d(M1,M2)＜η1，有：

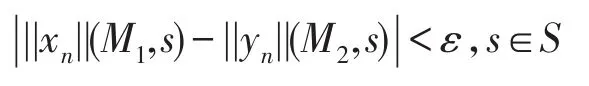
对于任意给定的ε>0，存在一个η2>0，使得只要d(M1,M2)＜η2，有：

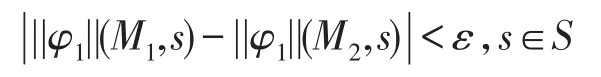
且对于任意给定的ε>0，存在一个η3>0，使得只要d(M1,M2)＜η3，有：

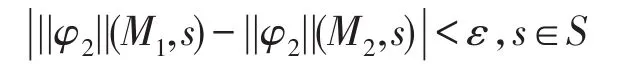
令η=min{η1,η2,η3}。因此对于任意给定的ε>0，存在一个η>0，使得只要d(M1,M2)＜η，有：

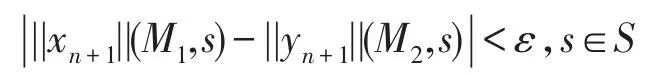
（7）当φ=＜＜A>>Gφ1时，由于证明过程类似于φ=＜＜A>>φ1Uφ2的证明过程，故省略证明过程。

5 结论

本文进一步研究了模糊交互时态逻辑的模型检测问题。通过将FATL的模型检测问题归约到经典的ATL模型检测问题，从而可以利用ATL的模型检测问题的研究结果来解决FATL的模型检测问题。另外使用这种归约方法，给出了FATL的模型检测问题的不动点迭代算法一个更精确的时间复杂性。研究了FATL语义的连续性，当模糊并发博弈结构发生微小变化时，模糊交互时态逻辑公式的语义也相应地发生微小的变化。本文所获得的研究结果为模糊开放系统的形式化验证提供了一种新的方法和理论指导。