图像插值空间自适应大容量无损信息隐藏算法*

熊祥光，陈 熙，曹永锋，欧卫华，刘 彬，夏道勋

贵州师范大学 大数据与计算机科学学院，贵阳 550001

1 引言

无损信息隐藏技术采用无损的方式将待隐藏的秘密数据隐藏在载体信号中，当需要时不仅可从隐秘载体信号中提取隐藏的数据，而且同时能完全恢复得到原始的载体信号，对失真敏感领域非常有用[1]。目前，已提出一系列无损信息隐藏算法，其大致可归为如下的3类：基于差值扩展[2-5]、基于直方图平移[6-9]和插值技术[10-19]。一般地，采用差值扩展和直方图平移的无损信息隐藏算法的隐秘图像质量都较好，但从单重隐藏性能来看，秘密数据隐藏容量很难达到1 bit/pixel及以上，而基于插值技术的无损信息隐藏算法与基于差值扩展和直方图平移的无损信息隐藏算法从原理上来说是不同的，该类算法直接在插值像素上进行，其主要思想是在图像插值阶段先对原始输入图像进行下采样（事实上不进行下采样操作也是可行的，进行下采样的主要目的仅是为了方便评估经图像插值和秘密数据隐藏操作后隐秘图像的质量），之后采用某种图像插值算法生成一幅插值图像（大小与原始输入图像相同）作为待隐藏秘密数据的载体图像；在隐藏秘密数据过程中，仅在插值图像的部分像素中隐藏秘密数据，在隐秘图像失真不可感知的条件下算法的秘密数据隐藏容量往往较大[10]。之后，文献[11]对文献[10]进行了改进，在相同条件下，可以隐藏更多的秘密数据，但这两种算法存在一个缺陷，就是仅当两个像素差值的绝对值不小于2时才能隐藏秘密数据，当差值为0或1时不能隐藏秘密数据，导致这两种算法的秘密数据隐藏容量受到影响。事实上，当两个像素差值为0或1时也是可以隐藏秘密数据的。文献[12]仅在插值图像部分像素中的每个像素隐藏1 bit秘密数据，与未隐藏秘密数据的插值图像相比，隐秘图像的质量较好，但秘密数据隐藏容量有限，最大仅为0.75 bit/pixel。文献[13]在文献[10-12]的基础上进行了改进，算法的秘密数据隐藏容量和隐秘图像质量都得到了提高，但是该算法的秘密数据隐藏容量和隐秘图像质量还有进一步提升的空间。文献[14-17]也是文献[10]的一种改进，秘密数据隐藏容量有了提高，但是通过实验发现，这四种算法都可能出现溢出现象。对于8 bit的灰度图像来说，采用这四种算法生成的隐秘图像像素的灰度值有时会出现溢出，使在秘密数据提取阶段算法不能正确地提取隐藏的秘密数据。文献[18-19]也分别提出基于插值技术的无损信息隐藏算法，但是这两种算法的秘密数据隐藏方式与文献[10-17]是不同的。实验结果表明，这两种算法的秘密数据隐藏容量和隐秘图像质量都较好。

为了进一步提高基于插值技术无损信息隐藏算法的秘密数据隐藏容量、隐秘图像质量和解决像素溢出问题，本文提出一种自适应的大容量无损信息隐藏算法，其创新之处主要是：（1）提出一种改进的图像插值算法，提高了插值图像的质量；（2）对插值图像中的待隐藏秘密数据像素，算法能自适应计算各个像素能隐藏的最大数据容量，使算法的秘密数据隐藏容量得到进一步的提高；（3）设计了新的秘密数据隐藏算法和根据隐秘图像与原始输入图像对应位置上像素差值绝对值的大小关系来自适应隐藏秘密数据，提高了隐秘图像质量和解决了像素溢出问题。在两个标准测试图像数据库上进行了大量的仿真实验，结果表明采用本文算法生成的隐秘图像不会出现像素溢出现象，可正确地提取在数据隐藏阶段隐藏的秘密数据。与同类算法相比，本文算法的秘密数据隐藏容量和隐秘图像质量都有了较大的提升。

2 基础理论

基于插值技术的无损信息隐藏算法主要包含图像插值和秘密数据隐藏两个过程，其图像插值过程示意图如图1所示[10]。

若原始输入图像X的大小为w×h，根据图1的图像插值过程示意图，本文提出的图像插值算法如下：

步骤1读取原始输入图像X，对其进行下采样操作，生成原始图像Y，相应的下采样操作可表示为：

其中，1≤p≤w/2，1≤q≤h/2。需要注意的是，进行下采样操作仅仅是为了便于测试经图像插值和秘密数据隐藏操作后的隐秘图像与原始输入图像X的失真情况。在实际应用时，可直接将输入图像X作为原始图像Y进行插值处理，此时生成的插值图像I大小为输入图像X的4倍。

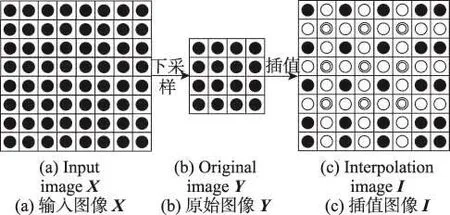
Fig.1 Schematic diagram of image interpolation图1 图像插值过程示意图

步骤2根据图1和步骤1得到的原始图像Y，生成插值图像I的算法如下：

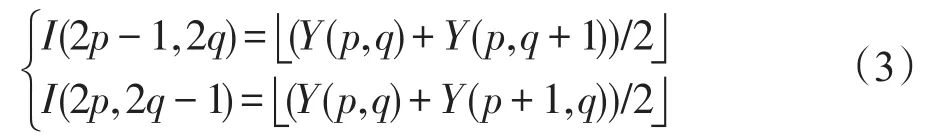
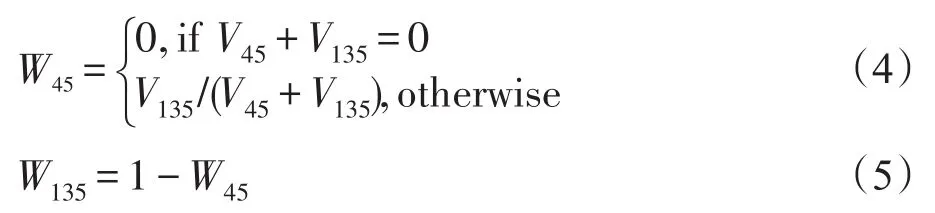
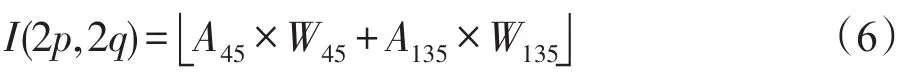
步骤3对于插值图像I的边界像素，采用周围的像素填充即可。

定义1将插值图像I中的像素划分为基准像素和非基准像素两类。对于如图1所示的图像，“”位置上的像素称为基准像素，在图像插值和秘密数据隐藏过程中都不会发生改变，也就是说它与输入图像对应位置上像素的灰度值相同。除“”位置上的像素外，其他像素称为非基准像素。在数据隐藏过程中，即在该类像素中隐藏秘密数据。

定义2对插值图像I，设基准像素为I(s,t)，与该基准像素相连的非基准像素I(u,v)与选择的基准像素I(s,t)差值的绝对值可表示为：

其中，I(u,v)∈{I(s,t+1),I(s+1,t),I(s+1,t+1)}，分别表示与基准像素I(s,t)相连的水平方向、垂直方向和对角方向上的3个非基准像素，表示求绝对值运算。非基准像素I(u,v)能隐藏的秘密数据量大小可表示为：

定理1对非基准像素I(u,v)，要使在秘密数据隐藏过程中它隐藏的数据容量nuv达到最大，则它与选择的基准像素I(s,t)的差值的绝对值duv就要取得最大值。

证明从式（8）可以看出，对于非基准像素I(u,v)，它能隐藏的秘密数据容量nuv为1或，与选择基准像素的差值duv大小相关。duv与nuv的关系如图2所示。从图2可以看出，差值duv和隐藏数据容量nuv虽不是严格的递增关系（因在计算各个非基准像素的隐藏容量nuv时，对其进行了向下取整运算），但要使非基准像素隐藏的数据容量nuv达到最大值，则在选择差值duv时就要选择最大的（若duv不是选择最大值，则nuv不一定能取得最大值）。

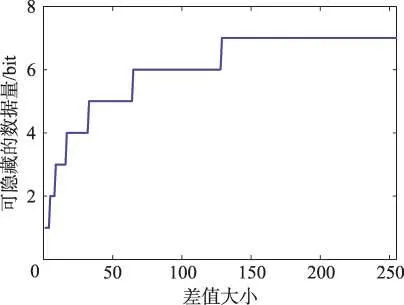
Fig.2 Relationship between difference and amount of data that can be hidden图2 差值与可隐藏数据量之间的关系

从式（8）和定理1可知，要使非基准像素能隐藏最多的秘密数据，非基准像素与选择的基准像素之间的差值就得最大。经图像插值运算后在非基准像素一定的条件下，要使它们之间的差值最大，选择的基准像素只能是所有基准像素的最大值或最小值。若未对插值图像进行分块，则插值图像中所有基准像素的最大值或最小值都是各个非基准像素的候选基准像素，在此情况下秘密数据隐藏容量应该取得最大值，但是隐秘图像质量失真也较严重。为了平衡秘密数据隐藏容量大小和隐秘图像质量间的关系，利用图像邻域像素的相关性，对插值后生成的图像I进行大小为m×m的分块处理。在秘密数据隐藏和提取过程中都是以各个独立的分块作为处理单元。大小为2×2、3×3和5×5的分块示意图如图3所示。在图3中，对于大小为2×2的分块，仅包含一个基准像素，对非基准像素计算差值时，该基准像素即为被选择的基准像素；对于大小为3×3的分块，包含4个基准像素，对非基准像素计算差值时，4个基准像素的最大值或最小值被选择作为各个非基准像素的基准像素；对于大小为5×5的分块，包含9个基准像素，对非基准像素计算差值时，9个基准像素的最大值或最小值被选择作为各个非基准像素的基准像素。需要注意的是，在对插值图像进行分块时应采用重叠的分块方式，且在秘密数据隐藏过程中每次仅对分块中与左上角基准像素相连的3个非基准像素进行操作。

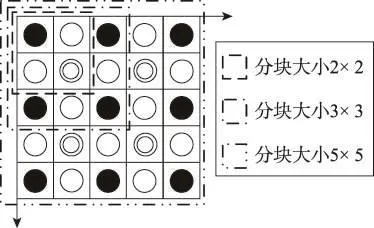
Fig.3 Schematic diagram of block图3 分块示意图

定义3对于非基准像素I(u,v)，从待隐藏的秘密数据中提取nuvbit的二进制数据，并将其转换为十进制数buv，隐藏秘密数据的公式可表示为：

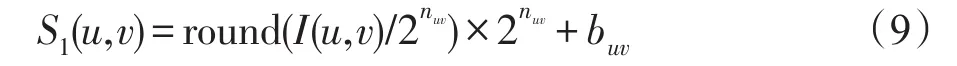
或

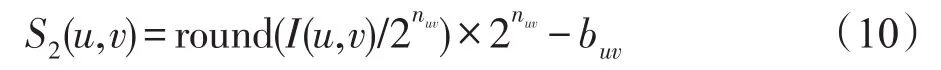
其中，round(·)表示四舍五入运算，非基准像素隐藏秘密数据后的像素灰度值S(u,v)=S1(u,v)或S(u,v)=S2(u,v)。

定理2在秘密数据隐藏过程中，无论是采用式（9）或式（10）隐藏数据，在秘密数据提取阶段，都能正确地提取出隐藏的秘密数据，计算buv的公式可表示为：

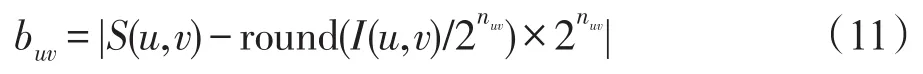
证明因为在秘密数据提取阶段，隐秘图像中基准像素的灰度值与原始输入图像对应位置上的灰度值相同，所以采用相同的图像插值算法后能生成相同的非基准像素I(u,v)。根据式（7）和式（8），各个非基准像素I(u,v)数据提取阶段和隐藏阶段的数据隐藏量nuv相同。从式（9）和式（10）可以分别得到buv=，也就是。在已知nuv和buv的条件下，将buv转换为nuvbit的二进制数据，即可得到隐藏的秘密数据。

定理3对于隐藏秘密数据后的隐秘图像S，与原始输入图像X相比，要使失真取得最小值，则隐秘图像分块中的非基准像素S(u,v)与输入图像对应分块中的像素X(u,v)的差值应取得最小值。

证明从定义3可以看出，隐秘图像中的非基准像素S(u,v)=S1(u,v)或S(u,v)=S2(u,v)。根据峰值信噪比（peak signal-to-noise rate，PSNR）的计算公式可知，PSNR值与输入图像和隐秘图像差值的平方成反比。因此，要使隐秘图像S具有较小的失真（更高的PSNR值），则隐秘图像S与原始输入图像X对应像素灰度值的差值就应该取得最小值。

在秘密数据隐藏过程中，为了使隐秘图像S与原始输入图像X对应像素灰度值的差值取得最小值，首先分别计算原始输入图像对应位置的像素灰度值与S1(u,v)和S2(u,v)的差值如下：

之后选择绝对值最小的修改方法作为该非基准像素的秘密数据隐藏方法。也就是说，若S1(u,v)与X(u,v)差值的绝对值小，则S(u,v)=S1(u,v)；否则S(u,v)=S2(u,v)。同时，为了使隐藏秘密数据后像素的灰度值不出现溢出现象（大于255或小于0），隐藏秘密数据的公式可表示为：

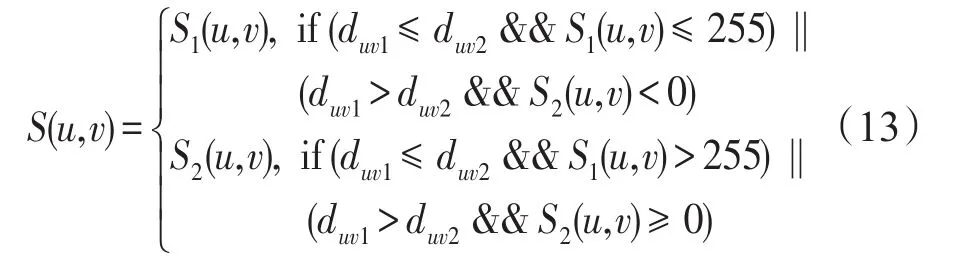
定理4对于8 bit的灰度图像，采用本文提出的图像插值和秘密数据隐藏算法后，隐秘图像像素的灰度值不会出现溢出现象。

证明对于8 bit的灰度图像X，其像素灰度值的范围为[0,255]。从图像插值过程可知，对于“”位置上的像素，与图像X对应位置上的灰度值相同，不会出现溢出现象；对于“”位置上的像素，其灰度值为图像X中相连两个像素灰度值的平均值，不会出现溢出；对于“”位置上的像素，均值A45和A135的范围为[0,255]，从式（4）和式（5）可知，W45和W135的范围为[0,1]，故采用式（6）得到的像素灰度值范围为[0,255]。从式（13）可知，无论S(u,v)=S1(u,v)或S(u,v)=S2(u,v)，其范围都在[0,255]之内，故隐秘图像中的像素灰度值不会出现溢出现象。

3 算法实施

基于第2章的定义和定理，本章首先介绍本文算法的详细实施方案，主要包括秘密数据隐藏过程、原始图像恢复过程和秘密数据提取过程。然后，从秘密数据隐藏容量、隐秘图像质量、算法的时间复杂度和空间复杂度四方面来对算法的性能进行理论分析。

3.1 数据隐藏过程

秘密数据隐藏过程的基本步骤如下：

步骤1读取原始输入图像X，采用本文提出的图像插值算法作用于下采样后的图像Y生成插值图像I，插值图像I作为待隐藏秘密数据的载体图像。

步骤2对输入图像X和插值图像I，按照从上到下，从左到右的顺序分别将其划分为m×m大小的重叠分块。需要注意的是，在对输入图像X和插值图像I分块的过程中，若载体图像的边界区域不能构成大小为m×m的分块，则这些边界区域不属于任何一个分块，在隐藏秘密数据时，这些边界区域可以隐藏秘密数据，也可以不隐藏秘密数据，对整个插值图像I可隐藏的秘密数据容量大小影响较小，可以忽略不计。

步骤3计算各个分块中所有基准像素的方差，根据所有分块方差的大小对其进行升序排序，得到所有分块对应的索引。在隐藏和提取秘密数据时，以此索引作为处理各个分块的顺序。需要注意的是，因为分块中的基准像素不会发生改变，所以在数据提取阶段计算各个分块的方差时，得到的结果与该步骤计算得到的结果相同，使在数据提取阶段处理各个分块的顺序与隐藏阶段相一致，确保能按顺序正确地提取隐藏的秘密数据。

步骤4利用步骤3得到的分块索引，按顺序每次读取一个分块，首先计算分块中所有基准像素的最大值Max与最小值Min，然后分别计算分块中非基准像素I(u,v)与最大值Max和最小值Min差值的绝对值如下：

步骤5对于分块中的非基准像素I(u,v)，它的差值duv可表示为：

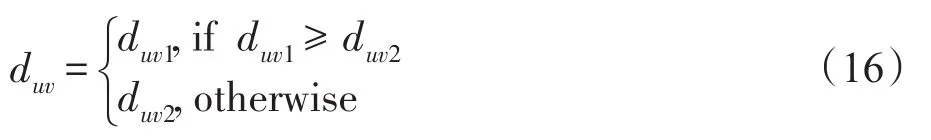
该非基准像素能隐藏的秘密数据容量大小采用式（8）来进行计算。

步骤6对于分块中的非基准像素I(u,v)，采用式（13）来自适应隐藏秘密数据。

步骤7重复步骤4～步骤6，当所有待隐藏的秘密数据或分块都处理完毕，秘密数据隐藏过程就结束，得到隐藏秘密数据后的隐秘图像S。

3.2 图像恢复和数据提取过程

原始图像恢复和秘密数据提取过程的基本步骤如下：

步骤1读取大小为w×h的隐秘图像S，按照从上到下、从左到右的顺序在隐秘图像S中位置为(2p-1,2q-1)（1≤p≤w/2，1≤q≤h/2）的像素点进行采样，即可生成大小为(w/2)×(h/2)的原始图像Y。

步骤2将提出的图像插值算法应用于步骤1恢复得到原始图像Y，生成与秘密数据隐藏过程相同的插值图像I。

步骤3与秘密数据隐藏过程中的步骤2和步骤3相同，得到所有分块的索引。

步骤4利用得到的分块索引，按顺序选择各个分块，首先计算分块中所有基准像素的最大值和最小值，然后分别利用式（16）和式（8）计算分块中各个非基准像素相应的差值大小duv和能隐藏的秘密数据容量大小nuv。

步骤5利用S(u,v)和I(u,v)，计算秘密数据隐藏过程中对I(u,v)的修改量大小，相应的计算公式可表示为：

步骤6先将buv转换为nuvbit的二进制数据，再将nuvbit的二进制数据按顺序连接，即可得到各个分块在秘密数据隐藏过程中隐藏的秘密数据。

步骤7重复步骤4～步骤6，将从各个分块中提取的二值数据按顺序进行连接，即可得到秘密数据隐藏过程中隐藏的秘密数据。

需要注意的是，步骤1生成的是输入图像X经下采样操作后生成的图像Y，而不是原始的输入图像X。实际应用时，可在图像插值阶段直接基于输入图像X进行图像插值操作，这样在图像恢复阶段即可完整地恢复原始的输入图像X。

3.3 算法性能比较

基于图像插值技术的无损信息隐藏算法其基本过程大致相同，一般都是由图像插值和秘密数据隐藏两个过程来组成。为了对不同算法的性能进行比较，从秘密数据隐藏容量大小、隐秘图像质量、算法的空间复杂度和时间复杂度等四方面对本文算法和文献[10-11,13]中的算法进行比较（文献[12]中的秘密数据隐藏算法与本文不同，文献[14-17]在隐藏秘密数据后有时会出现溢出现象，故未与这五种算法进行比较）。

3.3.1 数据隐藏容量

设输入图像X的大小为w×h，则经过图像插值后生成的图像大小也为w×h。在插值图像I中，非基准像素个数为(3×w×h)/4，在插值图像中可隐藏的总的数据容量为：

3.3.2 隐秘图像质量

基于图像插值技术无损信息隐藏算法的隐秘图像质量不仅由秘密数据隐藏操作来决定，而且图像插值操作对隐秘图像质量的影响也较大。一般地，对于纹理丰富的输入图像，因相连像素间的差异较大，根据图像插值算法生成的插值图像像素与输入图像像素的差异就较大，插值图像的质量下降较严重；反之，对于较平滑的输入图像，相连像素间的差异较小，根据图像插值算法生成的插值图像像素与输入图像像素的差异就较小，插值图像的质量下降就不是很明显。同时，该类算法在原始图像恢复过程中，仅需对隐秘图像进行下采样操作。因此，在秘密数据隐藏过程中，若考虑隐秘图像像素与原始输入图像对应位置像素间的大小关系，自适应地隐藏秘密数据，可能会提高隐秘图像的质量。文献[10-11,13]在隐藏秘密数据的过程中，都未考虑采用自适应的方式来隐藏秘密数据。因此，在相同的条件下，本文算法因为采用了自适应的秘密数据隐藏算法，所以本文算法的隐秘图像质量应该是最好的。

3.3.3 空间复杂度

基于图像插值技术的无损信息隐藏算法主要由图像插值过程和秘密数据隐藏过程组成。在图像插值过程中，文献[10-11,13]和本文算法的空间复杂度都为O(w×h)；在秘密数据隐藏过程中，文献[10-11,13]和本文算法都是直接在插值图像空间域中进行操作，空间复杂度都为O(w×h)。然而本文算法还需保存插值图像中所有分块的方差，空间复杂度为O(w×h)。因此，虽然这四种算法的空间复杂度都为O(w×h)，但是本文算法的空间复杂度是略高于文献[10-11,13]的。

3.3.4 时间复杂度

文献[10-11,13]和本文算法的时间复杂度都是取决于图像插值过程和秘密数据隐藏过程。在图像插值过程中，这四种图像插值算法的时间复杂度都为O(w×h)；在秘密数据隐藏过程中，这四种秘密数据隐藏算法的时间复杂度也都为O(w×h)。然而本文算法首先还需对插值图像中所有分块的方差进行计算，然后再进行排序操作，时间复杂度为O(w×h)。因此，虽然这四种算法的时间复杂度都为O(w×h)，但是本文算法的时间复杂度是略高于文献[10-11,13]的。

4 实验结果及分析

为了验证本文算法性能，实验平台为Windows 7操作系统和Matlab 2010a开发环境，待隐藏在插值图像中的秘密数据为伪随机产生的二进制数据。选择在非压缩图像数据库（never-compressedimagedatabase，NCID）[20]和南加利福尼亚大学信号与图像处理研究所图像数据库（USC-SIPI image database，SIPI）[21]中随机选择100幅载体图像进行实验。为了提高算法的运行效率，若图像数据库中的原始载体图像为彩色图像，则先将其转换为灰度图像。显然，在彩色图像的各个通道中都隐藏秘密数据也是可以的；若原始载体图像的大小不是256×256，则先将其转换为256×256，两个图像数据库中载体图像的基本参数如表1所示。在NCID和SIPI图像数据库中随机选择100幅载体图像验证了采用本文算法生成的隐秘图像没有出现像素溢出现象，能正确地提取隐藏的秘密数据。

为了能定量评估本文算法的性能，采用比特率（bit per pixel，BPP）来客观评判秘密数据隐藏算法真正能隐藏在一幅载体图像中的数据容量大小。计算BPP值的公式可表示为：

Table 1 Basic parameters of cover image in NCID and SIPI image databases表1 NCID和SIPI图像数据库中载体图像的基本参数

4.1 分块大小对算法性能的影响

本文算法在隐藏秘密数据的过程中需对插值后生成的插值图像进行重叠分块。为了测试不同分块大小对本文算法性能的影响，实验过程中，分别将插值后生成的插值图像分成互不重叠的2×2、重叠的3×3和5×5进行实验，相应的实验结果如表2所示。从表2可以看出：（1）当分块大小为2×2和3×3时，在插值图像中隐藏最大容量的秘密数据后，隐秘图像质量比未隐藏秘密数据的插值图像质量还好，其原因主要是因为在隐藏秘密数据过程中，算法考虑了隐秘像素与输入图像对应位置像素之间的关系选择了自适应的隐藏方法。（2）分块大小越大，隐藏的秘密数据量BPP值也就越大，但隐秘图像的PSNR值相应地下降了，其原因主要是因为分块越大，分块中候选的基准像素就越多，可隐藏秘密数据的非基准像素与候选基准像素最大值或最小值的差值就越大，使隐藏的秘密数据容量BPP值增大，但是因为基准像素与选择的非基准像素的差值较大，导致对非基准像素的修改量也较大，使隐秘图像的PSNR值下降了。当分块大小为2×2时，隐秘图像的PSNR值最高，但秘密数据量BPP值较低；当分块大小为3×3时，隐秘图像的平均PSNR值与分块大小为2×2时相比约下降了0.5 dB，但平均BPP值约提高了0.8；当分块大小为5×5时，平均BPP值约提高了0.5，但平均PSNR值与分块大小为3×3时相比约下降了1.7 dB。

在相同的实验条件下，首先对插值图像分别进行大小为2×2、3×3和5×5的分块，之后以BPP值0.1为初值和0.1为步长进行实验测试，相应的实验结果如图4所示。从图4可以看出，在NCID和SIPI图像数据库随机选择的100幅载体图像中当BPP小于0.9时，分块大小为2×2的PSNR值最好，但是随着BPP不断增大，PSNR值下降较快；对大小为3×3和5×5的分块，多数情况下PSNR值较接近。因此，综合表2和图4的实验结果，本文算法在对插值图像进行分块时将分块的大小设置为3×3。

Table 2 Effect of different block sizes on proposed algorithm performance表2 不同分块大小对算法性能的影响

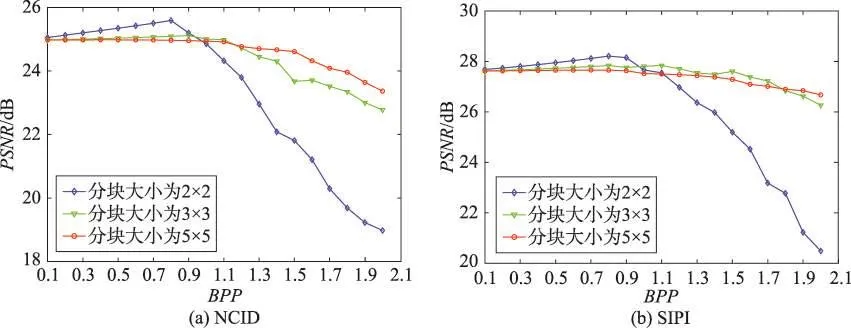
Fig.4 Effect of different block sizes on proposed algorithm performance图4 不同分块大小对算法性能的影响

4.2 算法性能比较

为了测试本文算法的优越性，将本文算法与文献[10-13,18-19]中的算法进行比较。表3给出了本文算法和这六种相似算法分别在NCID和SIPI图像数据库上随机选择100幅图像的实验结果。从表3可以看出，与文献[10-13,18-19]中的算法相比，本文算法的PSNR值和BPP值都是最高的，表明本文算法具有更优越的性能。

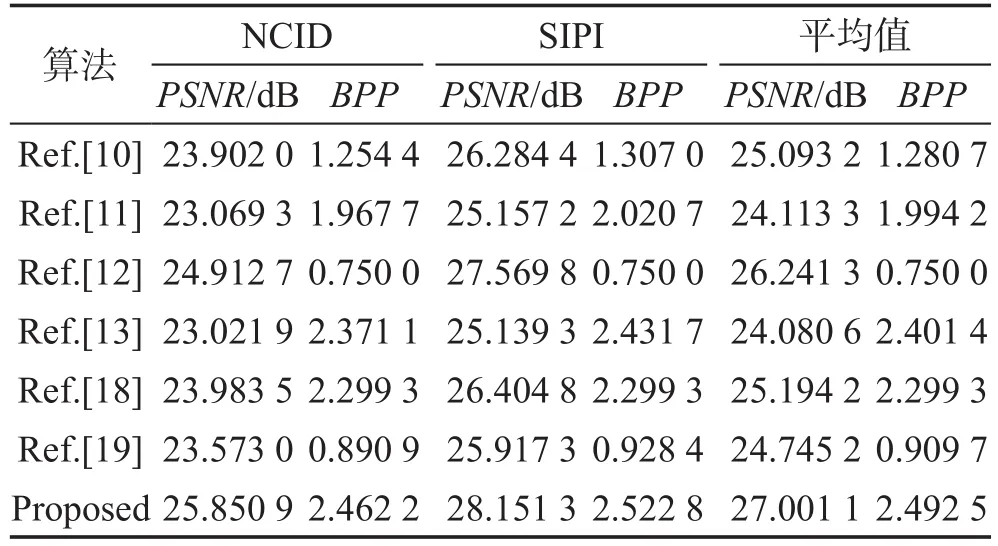
Table 3 Performance comparisons of proposed algorithm and other algorithms表3 本文算法与其他算法的性能比较

表4给出了本文算法和文献[10-13,18-19]分别在NCID和SIPI标准测试图像数据库上的性能提高情况。从表4可以看出，与文献[10-13,18-19]中的算法相比，平均PSNR值分别提高了约8%、12%、3%、12%、8%和10%，平均BPP值约分别提高了95%、25%、232%、4%、9%和174%。就其平均值而言，与这六种算法相比，平均PSNR值和平均BPP值约分别提高了9%和90%。

为了测试PSNR值和BPP值的离散程度，表5给出了本文算法与文献[10-13,18-19]分别在NCID和SIPI标准测试图像数据库上随机选择100幅图像实验结果标准方差的平均值。从表5可以看出，这七种算法在两个标准测试图像数据库上的标准方差都很相似，PSNR值和BPP值的离散程度都很好。

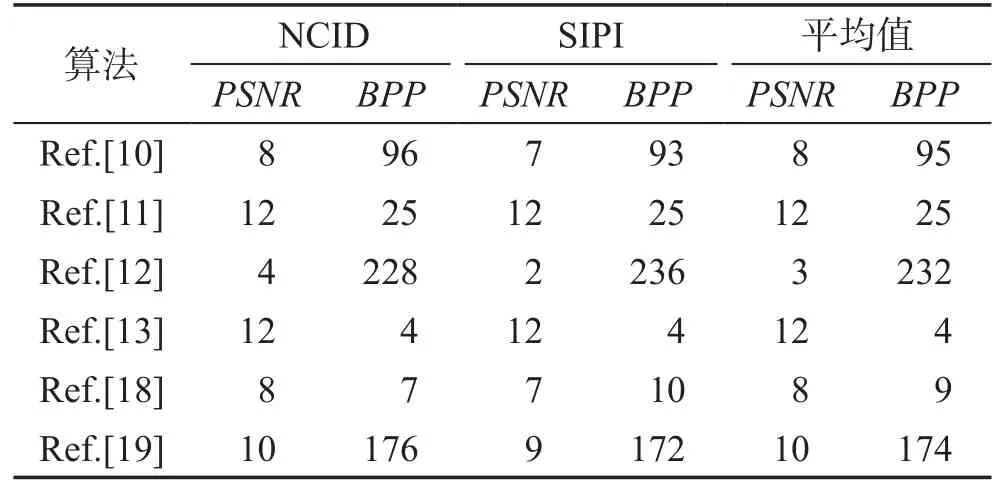
Table 4 Increase rate of proposed algorithm compared with other algorithms表4 本文算法与其他算法相比的提高率 %

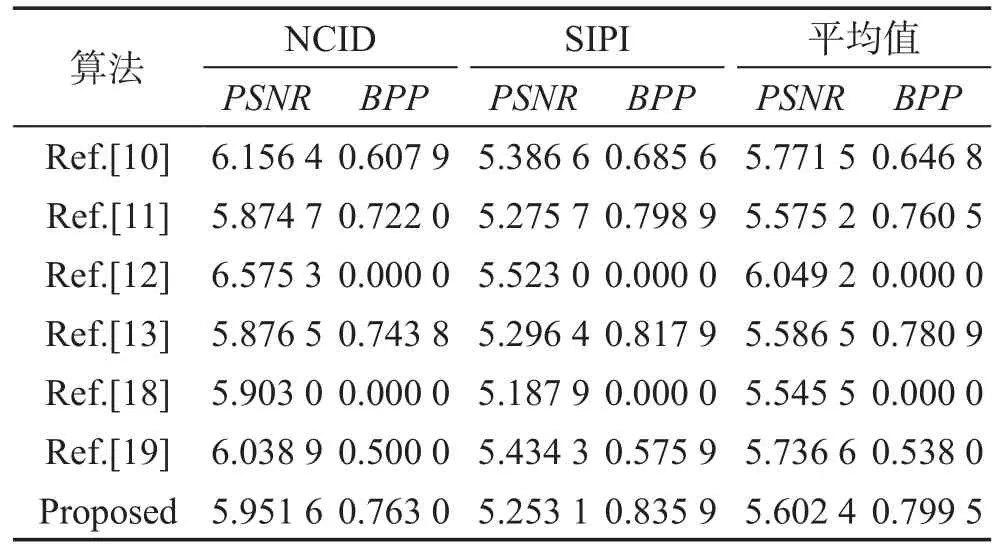
Table 5 Standard deviation of proposed algorithm and other algorithms表5 本文算法与其他算法的标准方差

另外，在相同的实验条件下，以BPP值0.1为初值和0.1为步长，将本文算法和文献[10-13,18-19]分别在NCID和SIPI标准测试图像数据库上进行性能比较，相应的实验结果如图5所示。需要注意的是，在实验过程中当计算某一个BPP值对应的平均PSNR值时，不是计算随机选择的100幅载体图像的平均值，而是仅计算能隐藏相应BPP值的隐秘图像的平均值。例如，当BPP为2.0时，若仅有30幅载体图像能隐藏此容量的秘密数据，则在计算平均PSNR值时，就只计算这30幅隐秘图像的平均PSNR值，而不是所有100幅载体图像的平均值。从图5可以看出，无论是在NCID或SIPI标准测试图像数据库，对于绝大多数的BPP，本文算法的PSNR值都是最高的，进一步表明本文算法性能更好。

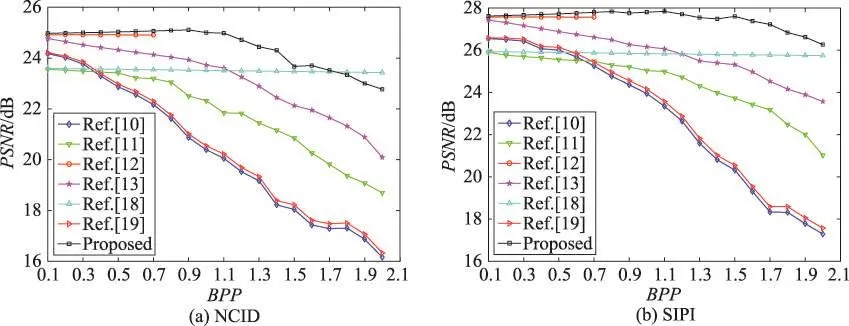
Fig.5 Performance comparisons for different algorithms on interpolated images图5 插值图像上不同算法的性能比较

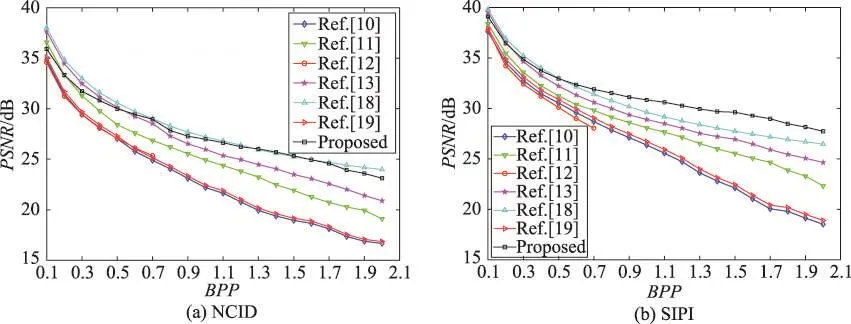
Fig.6 Performance comparisons for different algorithms on input images图6 输入图像上不同算法的性能比较

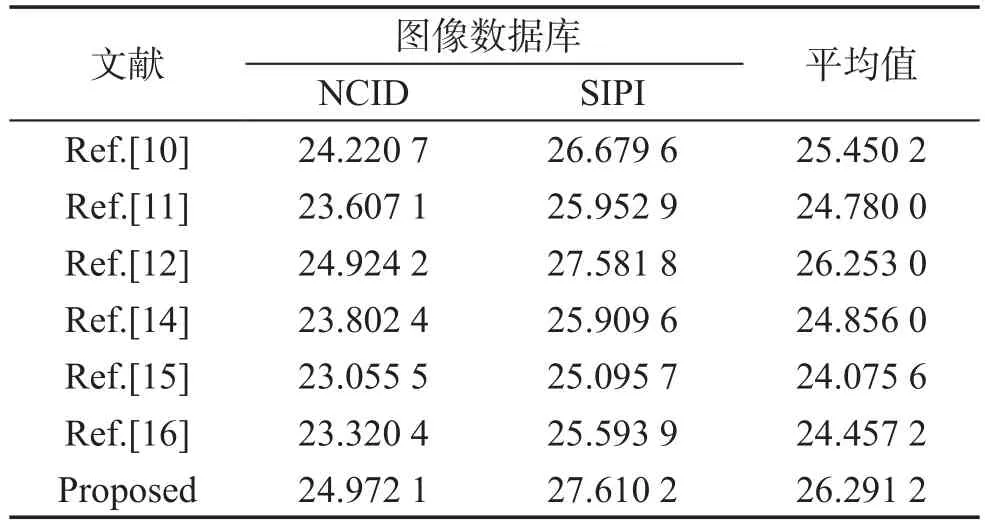
Table 6 Performance comparisons for different interpolated algorithms表6 不同插值算法的性能比较 dB

与图5在插值图像上进行秘密数据隐藏操作不同，图6给出的是本文算法与文献[10-13,18-19]在NCID和SIPI标准测试图像数据库输入图像上的性能比较（图像插值操作和秘密数据隐藏操作同时进行）。从图6可以看出，与这六种算法相比，无论是在NCID或SIPI标准测试图像数据库，对于绝大多数的BPP，本文算法的PSNR值都是最高的，表明本文算法具有更优越的性能。

为了进一步测试本文图像插值算法的性能，将本文图像插值算法与文献[10-12,14-16]中的图像插值算法进行比较，相应的实验结果如表6所示。从表6可以看出，无论是哪个图像数据库，在相同的条件下本文图像插值算法的PSNR值都是最高的，表明本文图像插值性能更好。

图7给出在相同图像插值算法条件下，采用本文秘密数据隐藏算法与文献[10-12]的比较。从图7可以看出，无论是哪个图像数据库，采用本文秘密数据隐藏算法后，隐秘图像的PSNR值都得到了提升，进一步表明本文提出的秘密数据隐藏算法具有更好的性能。

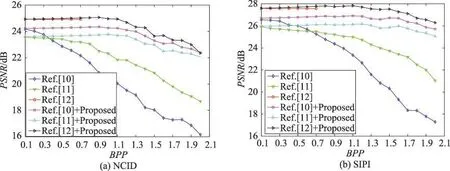
Fig.7 Performance comparisons for different hiding methods on interpolated images图7 插值图像上不同隐藏算法的性能比较

4.3 算法运行时间测试

本文算法和文献[10-13,18-19]中的算法都是在图像插值空间域中隐藏秘密数据，主要包含图像插值和秘密数据隐藏两个基本过程。为测试这七种算法的平均运行时间，在Windows 7和Matlab R2010a平台上进行实验，CPU为Intel®CoreTMi5-4200U，主频为1.60 GHz和2.30 GHz，内存容量为4.00 GB(2.45 GB可用)，硬盘容量为500 GB的测试环境下，分别在NCID和SIPI图像数据库中随机选择100幅图像(若原始图像为彩色图像，则先将其转换为灰度图像；若原始图像的大小不是256×256，则先将图像的大小调整为256×256)进行实验。在相同条件下，各种算法运行10次的平均运行时间如表7所示。从表7可以看出，文献[12]的平均运行时间最小，本文算法的平均运行时间最大，与第3.3.4小节中的理论分析是相一致的。

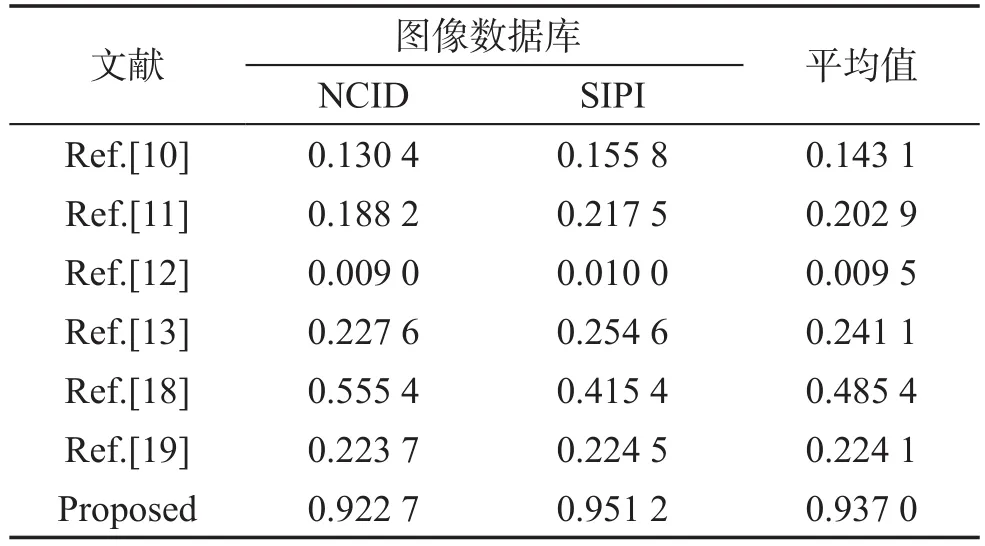
Table 7 Running time for different algorithms表7 不同算法的运行时间 s

5 结论

与基于差值扩展和直方图平移的无损信息隐藏算法不同，本文基于图像插值技术，提出一种自适应的大容量无损信息隐藏算法，具有如下的特点：

（1）提出一种改进的图像插值算法，与相似的图像插值算法相比，具有更好的性能。

（2）对待隐藏秘密数据的插值图像进行重叠分块，然后对分块中的各个非基准像素自适应计算它能隐藏的最大秘密数据容量大小，提高了各个非基准像素能隐藏的秘密数据容量。

（3）采用自适应的秘密数据隐藏算法来隐藏秘密数据，提高了隐秘图像的质量和解决了像素溢出问题。

在NCID和SIPI标准测试图像数据库上进行了大量的仿真实验，结果表明与相似的无损信息隐藏算法相比，本文算法的平均BPP值提升了约90%，平均PSNR值提升了约9%，在相同的BPP值条件下，本文算法具有更高的PSNR值；将本文提出的秘密数据隐藏算法应用于其他图像插值算法生成的插值图像，隐秘图像的PSNR值也得到了提高，进一步表明本文提出的秘密数据隐藏算法具有更优越的性能。