差分隐私下满足一致性的轨迹流量发布方法*

张双越，蔡剑平，田 丰，吴振强+

1.陕西师范大学 计算机科学学院，西安 710119

2.福州大学 数学与计算机科学学院，福州 350116

1 引言

随着移动互联网和GPS定位技术的发展，移动对象不断上传的位置信息形成了轨迹大数据。根据轨迹数据所含的丰富时空信息可以挖掘分析出许多人类行为模式和交通演化规律[1]。在路网交通背景下，对车辆轨迹数据中各个统计指标的发布可为道路管理及应急规划提供有力支持。例如，发布轨迹流量指标的统计信息可反映出每条路段的拥堵程度以及流量特征，这对于用户出行，交通指挥，乃至路网结构调整及整个路网的承载能力和可靠性的提高都有重要的现实意义和应用价值[2-3]。

然而，轨迹数据中隐含了用户的出行习惯、行为模式等隐私信息[4-5]。因此，直接发布轨迹流量值可能造成用户隐私泄露。例如，假设攻击者掌握了某个特定时段内除目标用户之外其他用户的轨迹信息，则他再结合所发布的轨迹流量数据即可追踪出目标用户在该时段内的轨迹。为了保护用户隐私，常用的轨迹发布隐私保护方法主要有假数据法[6-7]、泛化法[8-12]、抑制法[13-15]。这些方法通常通过变换或剔除轨迹中的敏感信息来保护轨迹数据的发布。但是，这些方法对攻击者拥有的背景知识敏感，容易受到背景知识攻击。当攻击者掌握了较多的背景信息时，用户的隐私就难以保障且缺乏严格的数学证明。2008年Dwork针对统计数据库的隐私泄露问题提出了差分隐私模型[16]。该模型保证了攻击者在任何知识背景下都无法准确地从所发布的数据中获得隐私信息且具有严格的概率分布不可区分性证明，引起了广大研究者的兴趣。2011年起，差分隐私模型被应用到轨迹发布隐私保护中，并取得了一系列成果[17-24]。但是，已有的工作专注于发布经过差分隐私保护的整个轨迹数据集，对路网环境下的轨迹流量发布缺乏考虑。本文在路网约束下结合差分隐私在保护统计信息领域的优势提出轨迹流量发布算法，并对该算法进行一致性优化，提高了发布结果的可用性和发布效率。

本文将路网结构抽象为有向图，有向图中的边连接两个相邻的路口，同时将轨迹数据相应地处理为形如图1（b）所示的有序序列，对这些轨迹数据进行统计即可得到路网中各个路段的轨迹流量。以北京某街区为例，图1（a）为该街区道路示意图，图1（b）为该示意图上的车辆轨迹数据样例。经统计得到的轨迹流量图如图2（a）所示。图2（a）中节点和边分别对应图1（a）中的各个路口和街道，边上的权值代表了相应路段的轨迹流量。接下来，在差分隐私机制下，向图2（a）中的边权值添加符合拉普拉斯分布的噪声以保护用户隐私。添加噪声后的流量图如图2（b）所示。不难发现，由于拉普拉斯噪声的引入导致了某些路口出入流量不一致的问题。如B路口所示（非起止路口），添加噪音扰动前车辆驶入该路口的次数等于驶出该路口的次数，如图2（a）都为3；添加噪音扰动后，该路口的驶入车次为4，驶出车次为3。这显然与实际情况不符。深入研究发现，不一致问题不仅导致发布结果不符合实际，同时也增大了发布误差。为此，本文提出了一种一致性调节方案来解决上述问题。

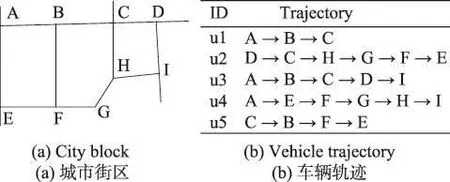
Fig.1 Vehicle trajectory from a city block图1 某城市街区及该街区的车辆轨迹

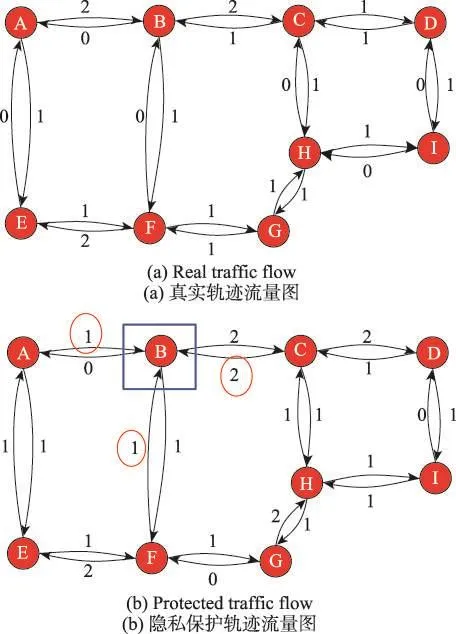
Fig.2 Traffic flow before and after protection图2 保护前后的轨迹流量图

对于差分隐私领域的不一致性问题已有学者进行了研究[25]。例如，Hay等人[26]对直方图发布中的不一致性问题提出了后置处理方案。然而由于研究目标不同，该方案无法直接应用于解决本文中的不一致问题。因此，本文在参考Hay等人[26]思路的基础上提出了一种新的后置调节算法。经过大量的理论分析以及实验表明，本文所提后置处理算法不仅能有效地解决上述不一致问题，还在合理的时间内对发布结果的精度有了明显提升。

综上所述，本文完成了以下工作：

（1）将实际城市路网抽象成有向图模型，并向图中引入一个辅助的虚拟节点。利用该虚拟节点形式化表现了流量图中的不一致性问题。

（2）结合拉普拉斯机制提出差分隐私流量图生成算法。

（3）在（2）的基础上提出一致性调节算法。该算法在严格的理论分析和公式推导下有效地解决了一致性问题，并提升了发布精度。

（4）在真实路网上对本文所提算法进行实验验证，结果表明一致性调节算法减小了约13%的发布误差且具有处理大规模数据的能力。

2 相关工作

为了解决轨迹数据发布过程中的隐私泄露问题，文献[17]首次引入了差分隐私机制。该文献利用原始轨迹数据的特性构建噪音前缀树，并向前缀树节点的计数值中添加拉普拉斯噪声保证用户的轨迹隐私。然而随着前缀树规模的增大，树中的节点将呈指数增长，导致落入每个分支的轨迹数量急剧减少，严重降低了数据可用性。随后文献[18]通过n-gram模型实现了可变长度的轨迹数据集发布，在一定程度上改善了文献[17]的不足。但是，文献[17-18]都基于一个共同的假设，即原始数据中存在大量的共同前缀，这在现实中很难满足。文献[20]利用指数机制对轨迹数据进行聚类操作，去除了轨迹数据中存在共同前缀的假设条件。文献[23]提出一种有界噪音泛化算法，减小了信息损失和平均轨迹合并时间。然而，以上文献都是发布经过差分隐私保护的整个轨迹数据集。文献[24]提出l-轨迹差分隐私保护模型，实时发布无限轨迹流上不同位置的用户统计值。然而却鲜有文献考虑路网约束下的轨迹统计值发布。文献[27]指出当发布大量用户位置的聚合信息时，差分隐私能提供较好的隐私保障。因此本文就以保护路网中的轨迹流量统计值作为切入点展开研究工作。

差分隐私中常见的优化方法主要分为基于数据压缩转换的前置优化算法以及基于规划策略的后置优化算法[26]。Hay等人[26]利用区间树的一致性问题对直方图统计发布进行优化就是一种典型的后置优化算法，该算法利用最优估计理论不仅解决了区间树的不一致性问题，同时还有效地提升了发布数据的可用性。在该理论的启发下，本文提出了一种新的优化模型，有效解决了轨迹流量发布过程中的不一致问题并提升了发布数据的有效性。

3 预备知识

3.1 基本概念

本文在论述过程中涉及到较多的数学符号，因此在介绍相关概念之前，先对这些符号进行说明，以方便读者理解。如表1所示。

定义1（路网拓扑图）将城市道路网抽象成一个有向图G=(V,E),其中V表示道路网中所有交叉路口的集合，E表示道路网中所有相邻交叉路口之间路段的集合。其相应的邻接矩阵记为M∈{0,1}|V|×|V|。其中，|V|表示集合V的大小，mu,v=1表示路口u和v之间存在边，否则不存在边。无特殊说明，以下将路网拓扑简称为路网。

定义2（轨迹空间）轨迹是移动用户产生的一系列位置vi按照时间排序构成的集合，记为L。本文对轨迹L进行预处理，使得L由所有它所经过的交叉路口表示，即∀vi,vj∈V，且每两个相邻节点所构成的边都属于边集E。由此可对轨迹空间Ω做如下定义：

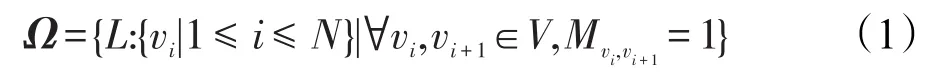
其中，N表示轨迹L的长度。

现实中的任何轨迹经过预处理后均是Ω中的一个元素。本文所用的轨迹数据集D是Ω的子集。根据轨迹数据集D和路网即可构建轨迹流量图。轨迹流量图定义如下。

定义3（轨迹流量图）根据轨迹数据集D计算出路网中每条边的权值，由此构成的有向加权图即为轨迹流量图。边u→v的权值表示轨迹数据集D中经过边u→v的轨迹数量。轨迹流量图中各个边的权值构成的流量矩阵记为。W即为本文发布的轨迹流量图。以下简称流量图。

3.2 差分隐私

定义4（差分隐私）假设存在一个随机算法A,SA表示该算法所有可能的输出构成的集合。则对于两个相邻的数据集D，D′(|DΔD′|≤ 1)以及SA，若算法A满足：

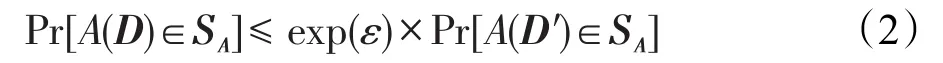
定义5（全局敏感度）对于任意函数f:D→Rd，全局敏感度表示向数据集中添加或删除一条记录，对函数f产生的最大影响。全局敏感度Δf可由以下公式计算：

其中，D和D′满足|DΔD′|≤ 1。

拉普拉斯机制[28]是常用的实现差分隐私的技术。它通过向查询结果添加符合拉普拉斯分布的噪音值来实现差分隐私。对于函数f:D→Rd，拉普拉斯机制实现差分隐私保护的过程可表示如下：

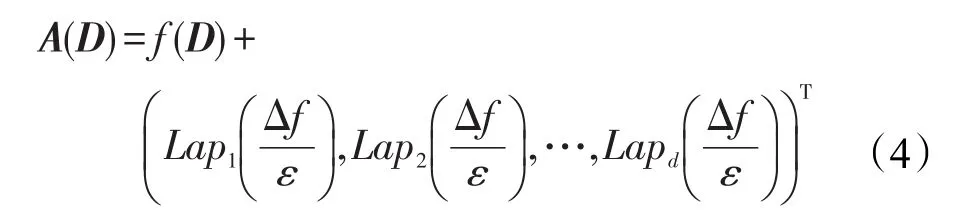
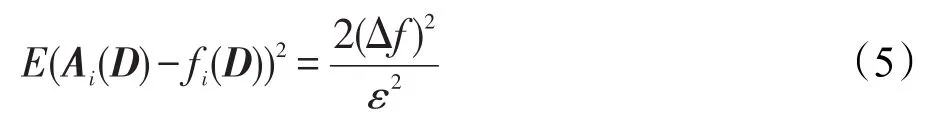
4 轨迹流量图发布

流量图的发布过程包括两步：（1）生成差分隐私流量图，即统计路网中各路段的流量值并添加独立同分布的拉普拉斯噪音；（2）一致性调节，即对（1）中的流量图进行出入流量一致性调节。下面分别描述这两个过程。

4.1 差分隐私流量图

轨迹流量图中节点的流入流量表示从各个方向驶向该节点的车次，而流出流量表示所有驶离该节点的车次。通过观察分析不难发现，当节点不是任何轨迹的起止点时，该节点的出入流量相等。为此，本文引入一个虚拟节点pv，并让该虚拟节点作为所有轨迹的起止点，使轨迹变为首尾相连的环，且虚拟节点与路网中每个节点都相连。虚拟节点的引入使得流量图中所有节点（包括虚拟节点）的出入流量都相等且不会影响真实流量图中各边的统计值。没有特殊说明，下文中的路网邻接矩阵M和流量矩阵W中均包含了虚拟节点。

4.1.1 差分隐私流量图算法

3．宋·天台金卞《游金庭观》：“寻真穷养浩，崇妙路迢迢。洞掩峰千叠，尘分水一条。白云生石壁，飞阁插崖腰。隐隐存仙迹，浑疑在碧霄。”[7]2426

使用差分隐私进行隐私保护前首先需要明确相邻数据集和全局敏感度。本文规定如果两个轨迹数据集D和D′仅相差一个位置点，则称两者为相邻数据集。因此，轨迹数据集D的相邻数据集D′（仍为Ω的子集）可通过删除或替换D中某条轨迹的一个位置点得到。删除方式引起的流量改变值为3，替换方式引起的流量改变值为4。由定义3可知，发布一个流量图的全局敏感度为4，即Δf=4。

差分隐私流量图算法描述见算法1。该算法的输入为轨迹数据集D，路网邻接矩阵M以及差分隐私预算ε；输出为真实的轨迹流量邻接矩阵W以及满足差分隐私的流量矩阵。算法1中首先初始化输出变量，2～5行对轨迹数据集进行处理，使每条轨迹的首尾与虚拟节点pv相连，然后统计路网中每个路段的流量值；6、7行向流量图中存在边的流量值添加噪音扰动，这是由于流量图中不存在的边不可能有轨迹经过，对其添加噪声保护没有意义；最后将流量矩阵返回。接下来对算法1的隐私性和误差进行分析。

算法1轨迹流量图发布

输入：轨迹数据集D，邻接矩阵M，隐私预算ε。

输出：加噪前后的流量矩阵W、。

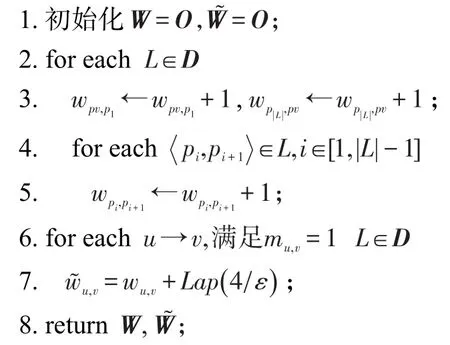
4.1.2 差分隐私流量图算法分析

本节首先证明差分隐私流量图算法符合差分隐私的定义，即算法1可以保证用户的轨迹隐私；然后分析该算法中由于差分隐私噪声的添加所引起的发布误差。用P:D→Rk代表差分隐私流量图生成算法，输入为轨迹数据集D，输出为实数域上的k维向量，k代表路网中所有的边数，其所有可能的输出结果为SP。D′与D是任意两个相邻的轨迹数据集，则对于任意的输出o(o1,o2,…,ok)∈SP有：

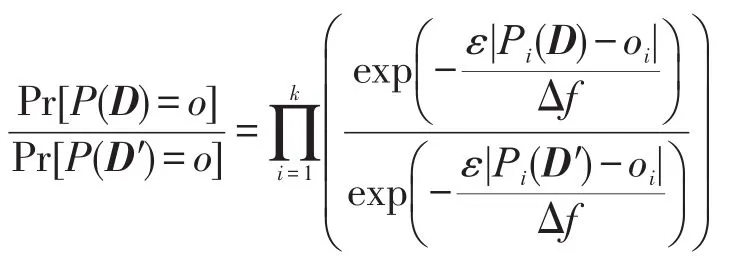
对其进行推导可得：

由前文关于差分隐私的定义可知，轨迹流量图发布算法符合差分隐私的定义。

接下来分析算法1中由于差分隐私噪声的添加引起的发布误差。根据式（5）可知，每添加一次拉普拉斯噪声将引起 2(Δf)2/ε2=2(4/ε)2的均方误差。算法1对路网矩阵M的每条边均添加拉普拉斯噪声。因此，的总体均方误差为 2(4ε)2×|E|，其中 |E|表示路网中所有的边数。由以上公式可知，算法1所发布的流量图误差大小取决于路网中边的数量以及用户设定的隐私预算ε，与轨迹数量没有关系。因此，在同一个路网中算法1所引起的误差不会随着轨迹数据集的改变而改变。

由于算法1对轨迹流量图中的每条边独立加噪，因此破坏了路网中节点出入流量相等的特性。针对这个问题，下面将通过二次规划求解，对算法1进行一致性调节。

4.2 一致性调节算法

如图2（b）所示，添加噪音扰动后的流量图大部分节点的出入流量不相等，虽然保护了用户的隐私，但是影响了发布数据的可用性。本节针对该问题提出算法2。对加噪后的流量图进行一致性调节,使得发布的流量图在满足差分隐私的同时具有较高的可用性。推导过程涉及了大量符号，符号说明见表1。

分别记一致性调节前后的流量矩阵为和，其元素分别表示为ij和ij。经分析发现，由得到的过程可转化为求解凸优化表达式（6）：

其中，I|V|+1表示长度为|V|+1（包含虚拟节点）且所有元素全为1的列向量。惩罚系数α2(α>>1)的引入是使得路网中不存在的边上的流量值在一致性调节后趋于0。因为当边i→j不存在时，若，则子式的值会非常大，而式（6）为了取得最小值就会迫使。极限情况下，当α→+∞时，有。为了式（6）表达更加紧凑，记惩罚系数矩阵为C，其元素满足。此时式（6）表示为：

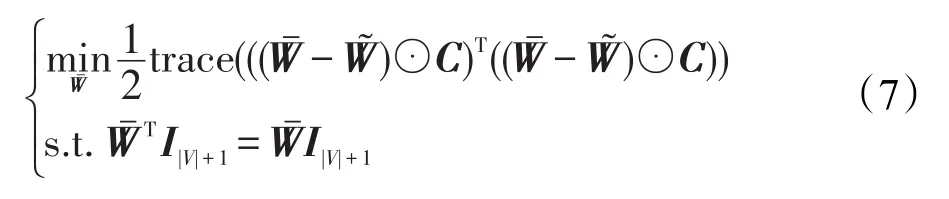
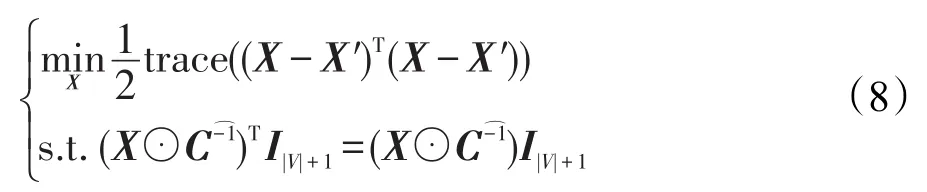
当α→+∞时，。因此，可使用邻接矩阵M来代替。同时将式（8）中的⊙运算部分利用普通乘法公式进行代换，得到与之等价的表达式（9）：

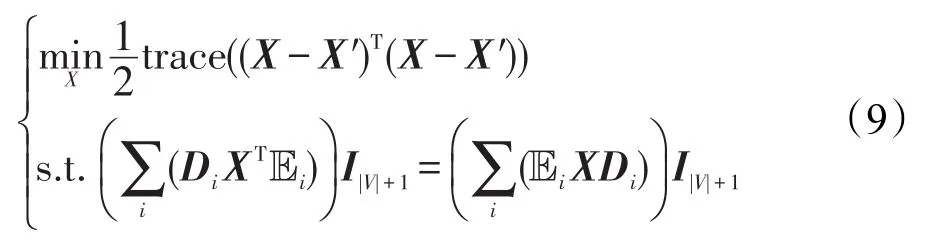
其中，Di表示取M的第i行向量并将其对角化后的常数矩阵；Ei为第i行以及第i列为1其他全为0的对角阵。此时。因此，式（9）解出的X即为式（6）的解。

接下来，为了求解式（9），使用拉格朗日乘子法将其转化为无约束的对偶问题。表示如下：

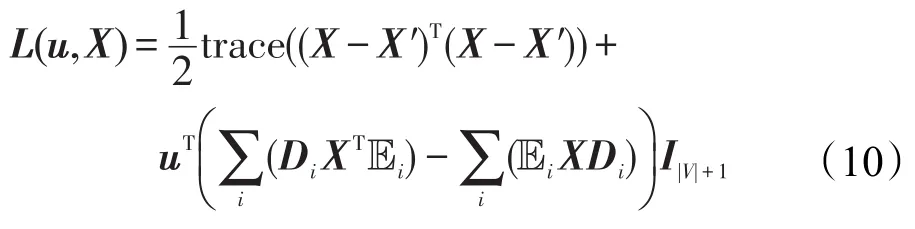
式中，u为拉格朗日系数组成的长度为|V|+1的列向量。对其化简可得：

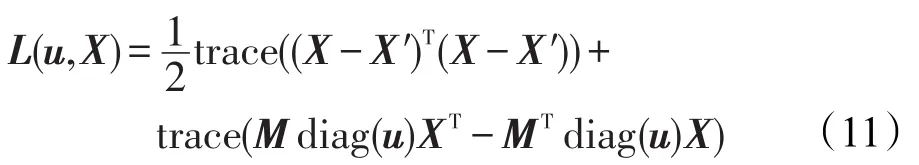
将式（11）对X求导，得到：

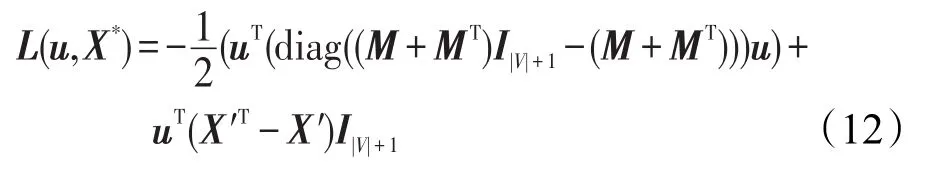
根据拉格朗日系数方法，L(u,X*)取得最大值的解即为式（6）的解。

接下来，求式（12）的最大值。不难发现该式为无约束的二次规划问题，令其二次项系数矩阵diag((M+MT)I|V|+1-(M+MT))为Q，Q为拉普拉斯矩阵，即不可求逆的半正定矩阵，由于M为连通图的邻接矩阵，因而其秩等于邻接矩阵的点数减去1。对式（12）求导可得：。根据Q的秩的性质，可采用将u的最后一个元素设为0求解。记′。同时由于路网邻接矩阵M中的虚拟节点pv与其他节点相连，将Q做如下分块，代入式（12）可得：

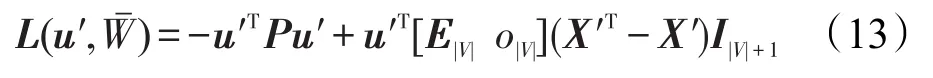
P为式（13）的二次项系数矩阵，对其分析可知该系数矩阵为正定矩阵。具体分析如下:

Q为半正定矩阵且，得，可知P′也是拉普拉斯矩阵，具有半正定性。因此，将任意非零列向量x代入下式有：

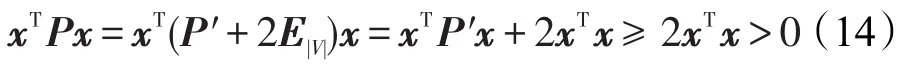
因此，P为正定矩阵。式（13）可直接求解得：

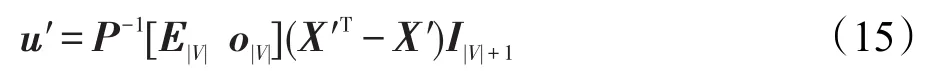
式（15）中求解u′的过程实际上就等价于解方程组Pu′=[E|V|o|V|](X′T-X′)I|V|+1。由于邻接矩阵节点数众多，而且极度稀疏。为使得式（15）具有更高效的求解效率，本文采用了PCG（preconditioned conjugate gradients method）。该算法是现有解决大规模稀疏方程组最有效的方法之一。由式（15）求得的结果u′即可得到u，由此求得一致性调节后的流量矩阵及最小误差分别为：

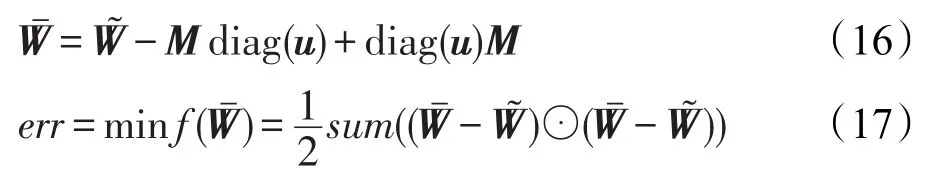
根据上述推导，最终得到一致性调节算法。

算法2一致性调节算法

输入：添加噪声保护的流量图，路网矩阵M。

输出：一致性调节后的流量图。

为保证算法效率，上述算法中的矩阵均采用系数矩阵存储并采用相关算法进行解释，具体过程文本不做进一步讨论。算法2的实现过程中采用了稀疏矩阵的数据结构及相关算法。关于稀疏矩阵的算法已经有诸多研究以及API的支持。本文在第5章提供了该算法的实现源码下载网址，供读者参考。

5 实验分析

本章主要从效用和执行效率两方面对本文提出的算法进行验证。实验的硬件环境为：Intel®CoreTMi7-6700 CPU@3.40 GHz，16 GB内存；用Matlab实现。实验中所用的路网分别来自德国奥尔登堡（Oldenburg）市，美国的圣华金（San Joaquin）以及旧金山湾区（San Francisco Bay Area）三个城市，相应的三个城市中的轨迹数据由Brinkhoff基于路网的轨迹生成器生成。Brinkhoff轨迹生成器和三个城市的路网信息数据可以从网站http://iapg.jade-hs.de/personen/brinkhoff/generator/下载。本实验中所用到的三个城市的路网信息以及相应路网上的轨迹详细信息如表2所示。其中，边的方向不同视为不同的边，路口数表示路网中交叉路口的数量。本章所涉及到的主要实验源码及部分供验证的数据已经上传到http://matweb.applinzi.com/paperCode/，供读者下载参考。本章实验包括三部分：（1）分析一致性调节前后算法1的相对误差；（2）采用标准误差具体分析一致性调节对算法1的优化情况，标准误差采用矩阵Frobenius范数计算，即；（3）对算法1和算法2的耗时情况进行分析。下面分别介绍这三部分。

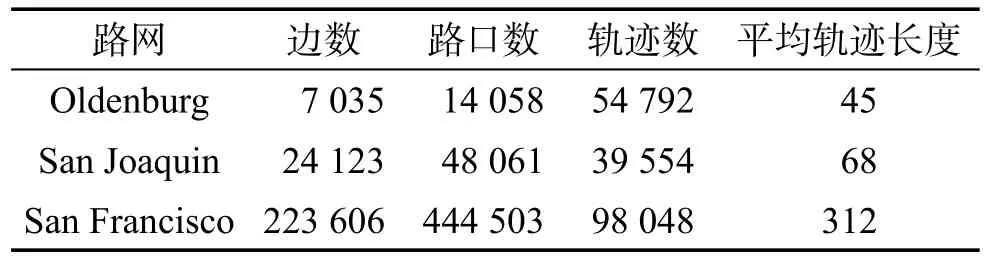
Table 2 Details of road network and trajectory表2 路网及轨迹信息

首先，采用奥尔登堡和圣华金的数据分别分析当隐私预算ε取1时不同轨迹规模下一致性调节前后的相对误差情况。相对误差通过公式求得。实验结果如图3所示。横坐标为轨迹规模，纵坐标为相对误差。从图中可以看出，同一路网中，随着轨迹规模的增大，相对误差逐渐减小，这是因为轨迹越多路网上流量值越大，相比之下噪音的影响就微乎其微。另外可发现，经过一致性调节后的相对误差明显比调节前的小。接下来具体分析一致性调节算法的优化程度。

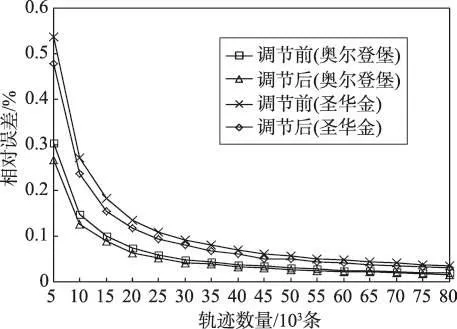
Fig.3 Relative error图3 相对误差

为验证算法2对流量图发布精度的提升情况，分别计算当ε取0.5、1.0、2.0、5.0时，三个城市一致性调节前后流量的标准误差，其结果如图4～图6所示。随着ε的增大，添加的噪音减小，相应的整体误差减小；随着路网规模的增加，添加噪音的次数增加，相应的整体误差增加，与4.1.2节的误差分析结果一致。另外可以看出，通过算法2的优化，整体误差减小了12%～14%，且减小的程度随ε的改变无明显变化，这说明算法2在不同的ε下是稳定的。

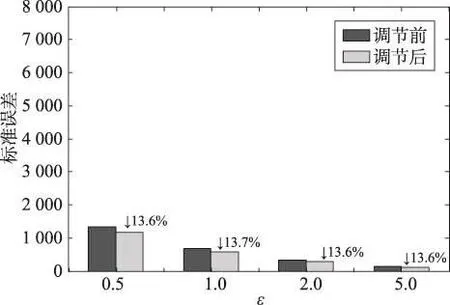
Fig.4 Error of trajectory flow before and after consistency adjustment in Oldenburg图4 奥尔登堡市一致性调节前后轨迹流量误差

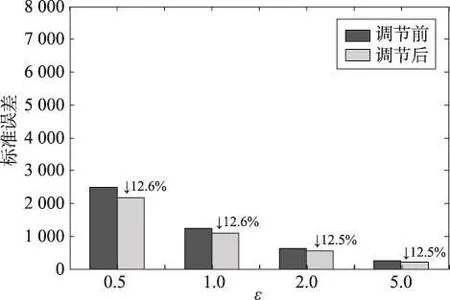
Fig.5 Error of trajectory flow before and after consistency adjustment in San Joaquin图5 圣华金市一致性调节前后轨迹流量误差

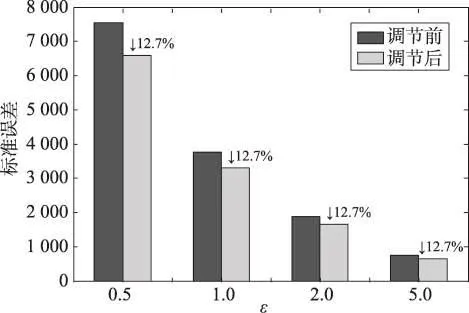
Fig.6 Error of trajectory flow before and after consistency adjustment in San Francisco图6 旧金山一致性调节前后轨迹流量误差

最后对算法1和算法2的耗时情况进行分析，仍以奥尔登堡市、圣华金以及旧金山湾区三个城市路网数据进行实验，实验结果如图7。结合表2可看出根据不同城市路网节点数、边数以及相应的轨迹规模的不同，算法1的耗时相差较大。尤其是路网规模最大的旧金山湾区，由于处理的轨迹数量为98 048条且平均轨迹长度为312，因此耗时达到了340 s左右。而算法2在优化上述三个城市的轨迹流量时用时均不到1 s。因此，本文所提出的一致性调节方法在提升轨迹流量发布效果的同时具有较高的发布效率且具有处理较大规模路网的能力。

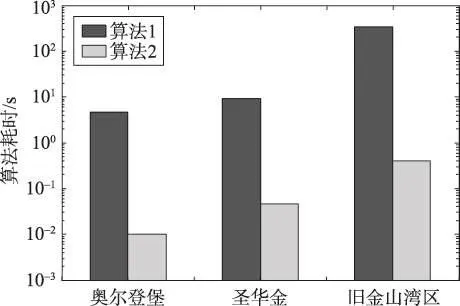
Fig.7 Run time图7 算法耗时

6 结束语

对蕴含路网信息的轨迹大数据进行分析，并发布一段时间内路网上车流量的统计值，可为现实中的很多应用提供参考信息。本文介绍了在差分隐私机制下发布基于路网的轨迹流量信息过程，并通过求解二次规划问题实现了流量图的后置处理算法。实验证明该一致性调节算法不仅提高了发布数据的精度，而且可处理较大规模的路网数据。但是，由于本文算法是针对于静态的轨迹流量图发布所设计的，无法满足现实中需要实时发布的应用场景。因此，如何将本文所涉及的算法与轨迹流量图发布的实时性相结合是下一步的研究方向。