三分解模型与算法及其在图像恢复中的应用*

杨章静，张凡龙，张 辉，杨国为，李佐勇 ，罗立民

1.东南大学 计算机科学与工程学院，南京 210009

2.南京审计大学 信息工程学院，南京 211815

3.南京理工大学 江苏省社会安全图像与视频理解重点实验室，南京 210094

4.闽江学院 物联网产业化与智能生产协同创新中心，福州 350108

1 引言

近年来，大规模的图像数据无时不在、无处不在，这为计算机视觉、模式识别、数据挖掘和机器学习等领域的发展带来机遇和挑战。这些图像数据含有丰富的信息以供挖掘利用，但与此同时，也大大增加了学习和研究的成本和困难，其中之一是在图像采集或处理过程中，往往受到各种噪声干扰。如何从观测到的含噪声图像中恢复真实图像对于后续应用意义重大。

为了恢复真实图像，在建模时必须诉诸于图像固有的低维结构。对于矩阵形式的数据，矩阵秩的大小可以直接反映这种低维性质，因此受到越来越多研究者的关注，其中鲁棒主成分分析（robust principal component analysis，RPCA）[1-2]是一种经典的基于低秩假设的模型。它假设数据矩阵具有低秩性并且误差矩阵是稀疏的。RPCA存在许多求解算法，如：乘子交替方向法[3]、梯度下降法[4]和基于随机优化的算法[5]。RPCA由于其可以扩展到处理部分数据丢失的情况，这实际上是矩阵补全问题的扩展，RPCA因此已经成功应用于视频背景建模、排名协同过滤和人脸识别等领域中。作为RPCA的重要扩展，低秩表示（low rank representation，LRR）[6-8]可以将数据分解为多个线性子空间的并集。与RPCA一样，LRR也假设误差项是稀疏的。

最近，有研究者[9]提出了基于双核范数的矩阵分解方法（double nuclear norm based matrix decomposition，DNMD），并得到进一步扩展和应用[10-12]。DNMD使用统一的低秩假设来表征真实图像数据和遮挡数据，它假设所有图像向量形成低秩矩阵，并且因遮挡导致每个误差图像也是低秩矩阵。与RPCA相比，DNMD的低秩假设对于描述遮挡更直观。

在此基础上，用于图像去噪的加权核范数最小化[13-14]和基于Transformed-L1最小化的压缩感知[15-16]相继被提出，它们都是仅限于低秩分量正好低秩，稀疏分量完全稀疏。但是，这些假设中的任何一个在实践中未必一定满足，应该予以松弛。为适应更复杂的噪音，Cao等人[17]通过假设噪声分布符合指数幂分布，提出了基于混合分布的恢复模型。在此基础上，Yao等人[18]提出了一种子空间聚类方法，该方法对各种噪声分布均具有鲁棒性。Hu等人[19]采用了一种新的矩阵范数，称为截断核范数，用于近似秩函数。为了揭示数据矩阵中的局部模式，Abdolali等人[20]提出了一种将数据矩阵分解为不同尺度的低秩分量的方法。Bouwmans等人[21]对这些不同问题的最新发展进行了综述。

以上提到的模型和方法均存在一个共同的局限：无法处理混合噪声。在噪声符合高斯分布的假设下，很自然地可以利用L2范数（F范数）作为噪声度量。为了避免L2范数对孤立点和非高斯噪声的敏感性，也可以用L1范数作为噪声度量。然而，L1范数仅仅在处理符合普拉斯分布的噪声时才是最优的，对处理各种混合噪声仍然非常有限。实际问题中遇到噪声并不单一，仅仅假设噪声符合某一种分布并不合理。

针对此问题，本文提出了一种三分解模型（tridecomposition model，Tri-Decom）用于恢复受到大的稀疏噪声和小的稠密噪声破坏的图像数据。该方法通过不同的度量函数分别对干净数据、稀疏噪声和稠密噪声进行刻画。此外，为了求解Tri-Decom，提出了乘子交替方向法。在人脸图像中去除遮挡和监控视频中进行背景建模的实验验证了所提出方法的有效性。

2 相关知识

给定数据矩阵X，记奇异值分解为X=USVT，其中S=diag(σ1,σ2,…,σr)，U和V是列正交矩阵。核范数、L2范数和L1范数分别定义为：

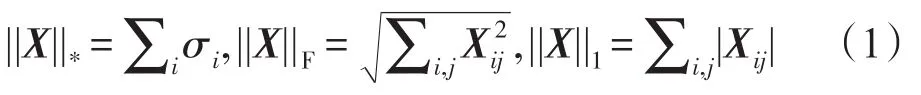
给定τ>0，奇异值阈值算子Dτ(·)定义为：

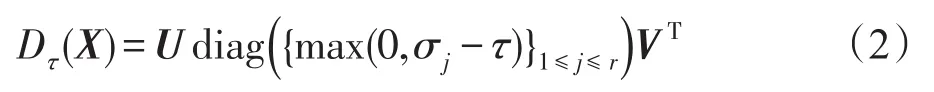
数据X通常被各种噪声破坏，包括大的稀疏噪声和小的稠密噪声。RPCA的基本思想是将X分解为两个矩阵D和E，其中矩阵D具有低秩性，而矩阵E具有稀疏性，其模型如下：

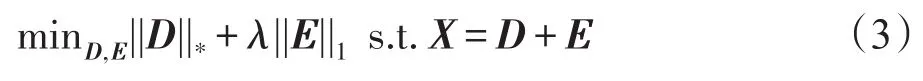
作为RPCA的重要扩展，低秩表示（LRR）可以将数据分解为多个线性子空间的并集。与RPCA一样，LRR也假设误差项是稀疏的。

最近，研究者[9]提出了基于双核规范的矩阵分解（DNMD），DNMD旨在将每个图像分解为Xi=Di+Ei。具体而言，给定图像X1,X2,…,Xs∈Rm×n，其模型如下：

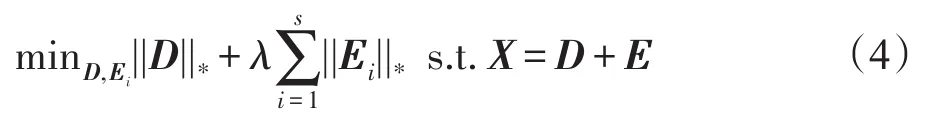
其中，X=[vec(X1),vec(X2),…,vec(Xs)]，D=[vec(D1),vec(D2),…,vec(Ds)]，E=[vec(E1),vec(E2),…,vec(Es)]。

3 三分解模型及其算法

首先给出如何将图像恢复问题表示为数据的三分解模型，然后具体介绍其算法。

3.1 三分解模型

根据以上分析，低秩分量正好低秩，稀疏分量完全稀疏。但是，这些假设中的任何一个在实践中未必一定满足，为此本文考虑添加一个新的分解项，它表示非稀疏的扰动误差（稠密误差）。例如，在监控视频中，可以将每一帧拉成一个列向量，然后将视频的所有帧按列排成一个矩阵，记为X。三分解的目的是将X分解为D、E和F三个分量。分量D代表视频背景，由于帧之间的相似性，一个合理假设是假设D具有低秩性；分量E表示视频中的活动目标，可以假设E具有稀疏性；分量F表示由光照、阴影或其他因素引起的扰动噪声。

为此，提出一种新的图像恢复方法，称为三分解模型（Tri-Decom）：

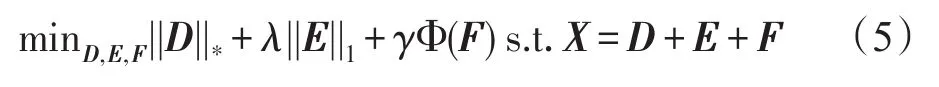
其中，原始数据X被分解为三个分量；分量D是低秩矩阵，代表恢复后的数据；分量E和F分别代表稀疏噪声和非稀疏噪声。

函数Φ(·)表示非稀疏噪声的度量方法，实际应用中，可以针对特定问题选择函数Φ的合适形式。本文下面的研究中选用，主要基于以下考虑：目标函数中的噪声项E代表了稀疏噪声，第三项F代表了因密集的小扰动引起的稠密噪声，而F范数在刻画稠密小噪声方面具有明显优势。另外，F范数具有连续可微性和凸性，利于后续求解。

Fig.1 Decomposing observation frameXiinto 3 partsDi,EiandFi图1 将观察帧Xi分解为Di、Ei和Fi三个分量

整个过程如图1所示。为可视化，在图中对Ei和Fi进行了二值化处理。将每一帧拉成向量后可以按列将所有视频帧组成一个矩阵，进而分别得到对应的X、D、E、F。

3.2 三分解算法

在统计学习和机器学习等领域诸多优化问题都有一个共同特点，即数据量大，导致对应的优化问题变量规模也大，而传统的许多优化方法无法直接应用于大规模变量，乘子交替方向法（alternating direction method of multipliers，ADMM）[3,22-23]是近年兴起的，行之有效的处理大规模优化问题的算法，尤其适合变量可分离的优化模型。故本文使用ADMM求解三分解模型。首先给出Tri-Decom对应的增广Lagrange函数如下：

其中，Y是Lagrange乘子矩阵，μ是罚参数。接着，采用交替方向法更新每个变量。算法框架具体如下：

（1）固定E=Ek,F=Fk,Y=Yk，更新D：

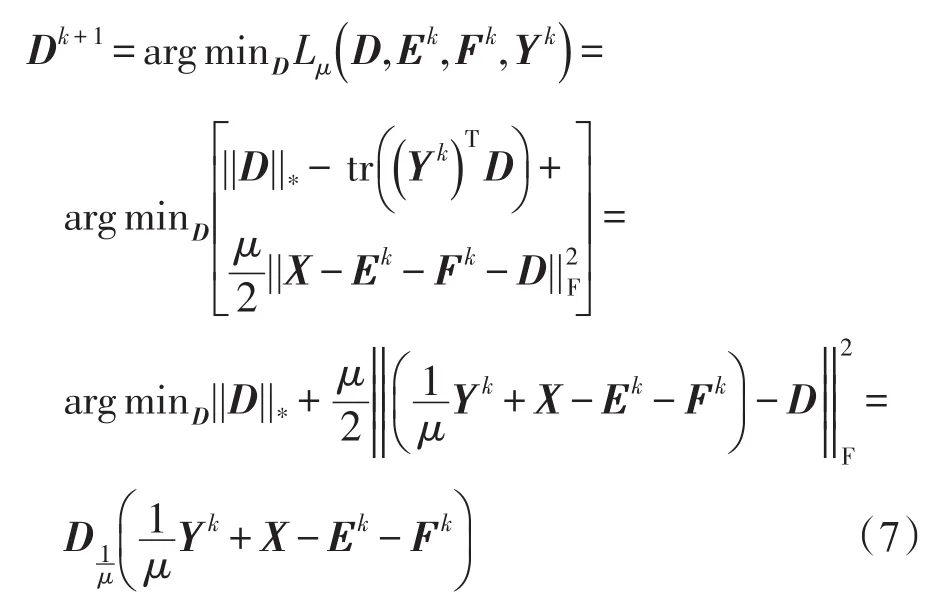
其中，Dτ(·)是由式（2）定义的奇异值阈值算子。

（2）固定D=Dk+1,F=Fk,Y=Yk，更新E:

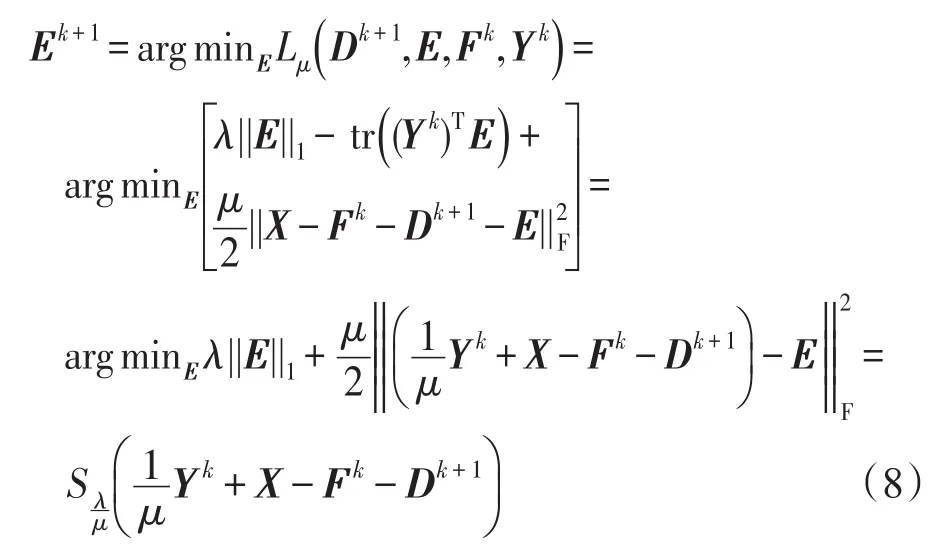
其中，Sε(·)是一个软阈值算子，其定义如下：

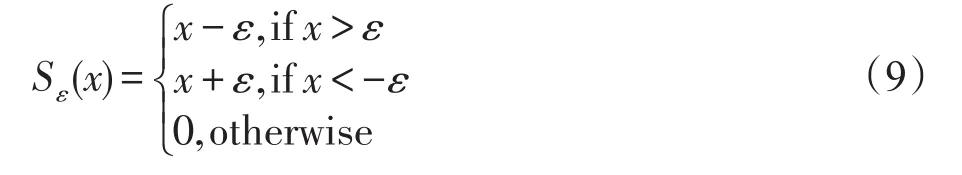
软阈值算子将绝对值小于ε的数全部置零，而将绝对值大于ε的数做一个特殊处理：大于ε的数统一减去ε，小于 -ε的数统一加ε。一组数字经过软阈值算子的作用之后会比较光滑，符合图像像素值连续变化的特点。具体到式（8）中ε=λ/μ。

（3）固定D=Dk+1,E=Ek+1,Y=Yk，更新F:

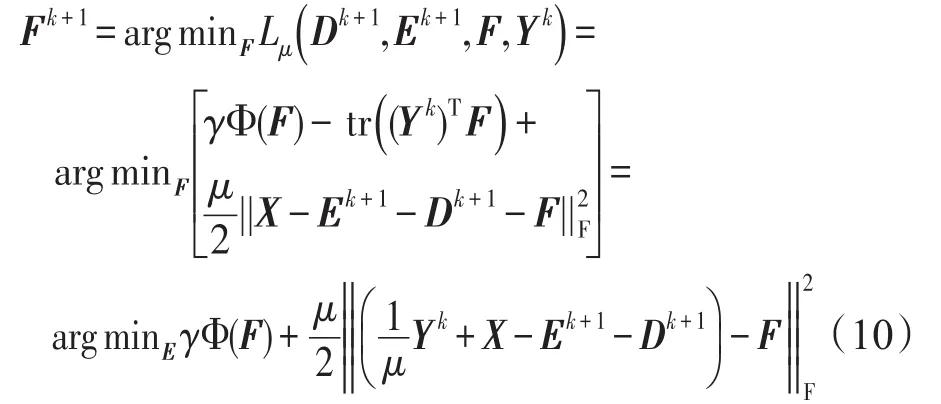
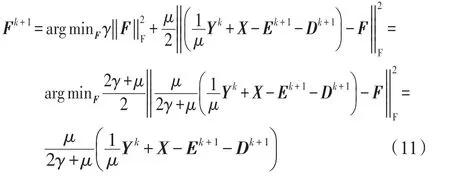
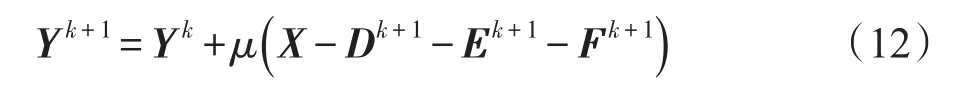
3.3 算法最优性条件分析

下面给出最优性条件和停止准则。三元组(D∘,E∘,F∘)是最优解的充要条件包括原始可行条件性与对偶可行性条件。其中原始可行性条件是指(D∘,E∘,F∘)要满足约束条件，即：

对偶可行性条件是指目标函数在(D∘,E∘,F∘)处的微分（或次微分）包含0点，即式（14）和式（15）：

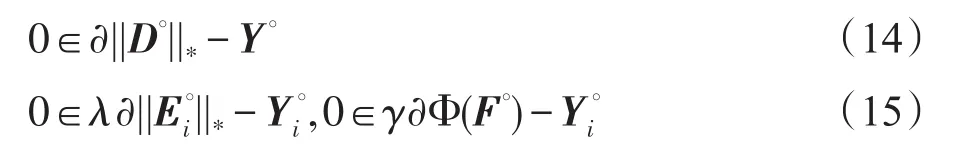
对于 式（13）,在第k+1步迭代时的残差X-Dk+1-Ek+1-Fk+1称为原始残差，记为rk+1。当原始残差小到某个阈值，则可认为(Dk+1,Ek+1,Fk+1)符合原始可行性条件。

下面考虑如何判定对偶可行性条件，由于Dk+1是Lμ(D,Ek,Fk,Yk)的极小点，因此可以表示如下：

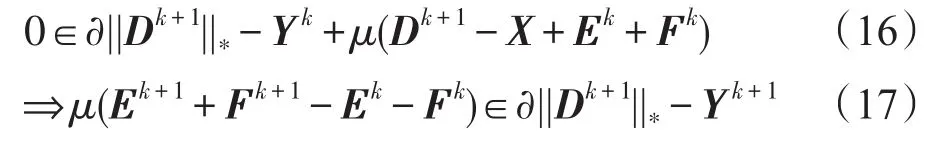
其中，μ(Ek+1+Fk+1-Ek-Fk)为对偶残差，记为sk+1。

在迭代过程中，对偶残差sk+1和原始残差rk+1收敛到0。一个合理的终止准则可以做如下选择：, 其中，εpri和εdual定义为：

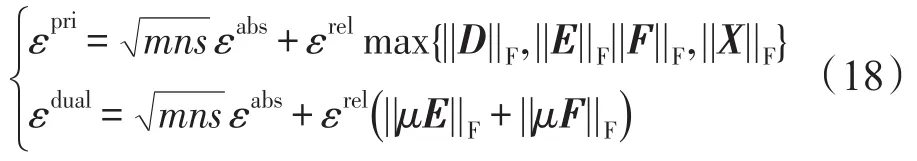
其中，εabs、εrel分别是绝对容差和相对容差。

三分解模型求解算法：

1.输入:观测数据D,参数λ、γ、εabs、εrel，进行初始化：

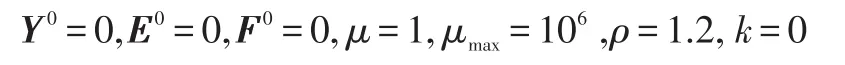
2.分别利用式（7）、式（8）和式（11），更新(D,E,F)；

3.利用式（12）更新乘子Y；

4.更新μ:μ=min(ρμ,μmax);

4 实验

为了验证算法的性能，将提出的算法应用于视频背景建模和人脸图像数据的恢复，作为对比，同时采用了其他典型算法如RPCA、RPCA-Lp[24]和DNMD。

4.1 参数分析

为了分析模型中的参数影响，以视频监控的背景建模为例。背景建模是计算机视觉应用中非常重要的主题。对于一段视频，将其中的每一帧拉成一个列向量，然后按列排成一个矩阵，记为X；通过各种算法对X中的背景和目标进行恢复。

Tri-Decom的两个参数λ和γ分别用于在噪声项和干净数据项之间保持平衡。作为评估不同参数值影响的说明性示例，使用100帧并将每一帧堆叠到矩阵X中，矩阵X的大小为4 800×100；接着通过Tri-Decom检测前景目标，实验结果如图2所示。

图2（a）中，对稀疏噪声E的稀疏性的测量可以看出：在λ不变的情况下，γ越小||E||1越小，也即E越稀疏；在γ不变的情况下，λ越大||E||1越小。因此λ与γ对稀疏性有截然相反的影响。同理，图2（b）～图2（d）清楚体现了λ与γ对稠密性噪声和矩阵秩的影响。从图2实验结果可以看出三个分量的测量值随着参数的不同而显著变化，这就说明引入的参数在提出的模型中起着关键作用。一般情况下，最优参数与不同数据集的属性有关，没有适用于不同数据库的一致规则。

4.2 视频背景建模

背景建模是从视频的背景中抽取出活动行为（也称前景目标）。背景建模在事件监测、人体行为识别中都扮演着重要角色[25]。

实验使用九段视频[26]（http://perception.i2r.a-star.edu.sg/bk_model）。对于每段视频，使用200帧，每帧的大小为60×80。将这些帧堆叠到矩阵X中，矩阵X的大小为4 800×200。为了进行量化评估，使用F-score来测量恢复精度，F-score定义如下：

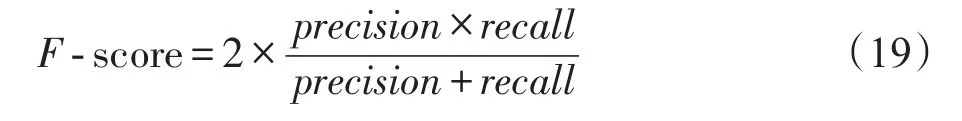
其中，precision=|G⋂T||T|,recall=|G⋂T||G|，G是真实行为，T是恢复后的行为。

Fig.2 Measure values of 3 decomposition terms versus different parameters图2 在不同参数下三个分量的测量值

实验具体指标结果见表1，F-score值越大，代表行为恢复得越准确。从表1可以看出，在大多数情况下，Tri-Decom明显优于其他方法，这验证了Tri-Decom对背景提取的有效性。图3显示本文方法的恢复结果。这里需要指出的是，为实现可视化，将恢复的活动和非稀疏噪声中的像素值进行了二值化处理。

由于光照变化（图3第1、2行）或水纹变化（图3第3行）所造成的噪声具有稠密性，而非稀疏性，这可从图3第（e）列的结果看出。与此同时，视频中的目标行为相对于整段视频，具有稀疏性，可视为稀疏噪声，这可从图3第（d）列看出。对比图3的第（d）、（e）两列，可以清楚看到本文的Tri-Decom能有效地识别稀疏噪声（即恢复的活动目标）和稠密噪声。

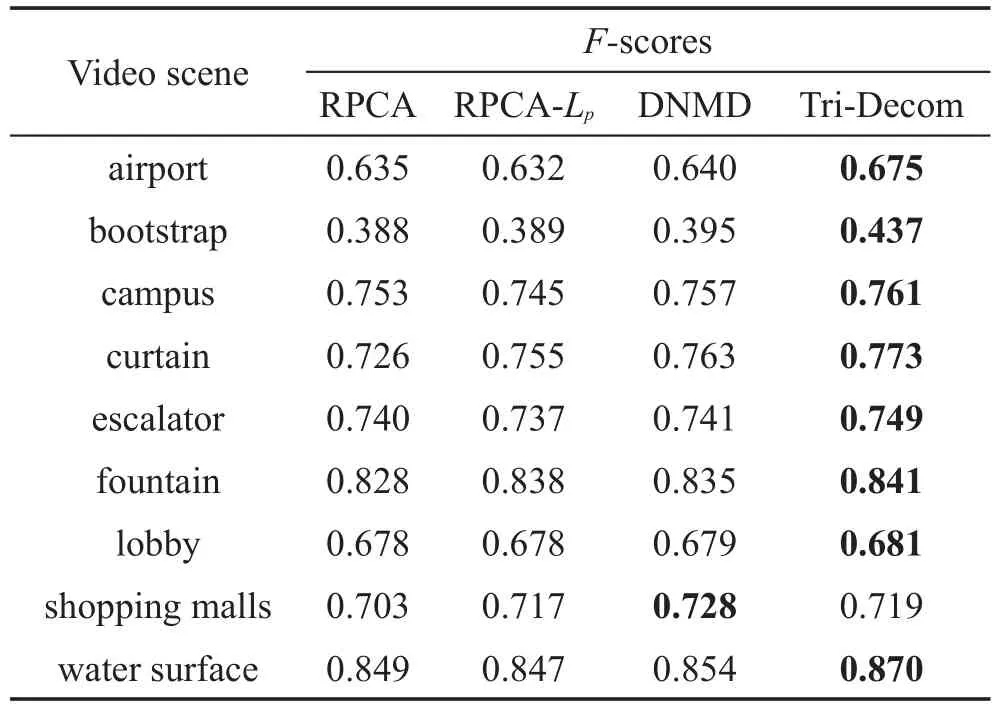
Table 1 F-score on 9 video surveillance表1 九段不同监控场景下的F-score值

4.3 人脸图像恢复

在实际应用中，采集到的人脸图像通常受到光照、遮挡等多种因素的干扰。因此，在进一步应用之前，需要从损坏的数据中恢复真实数据。这些误差通常包括大幅度的稀疏噪声和小幅度的稠密噪声。正如文献[1,9]中指到的，如果有同一个个体的足够多的图像，基于低秩假设的模型能够完美恢复损坏的数据。

在Extended Yale B数据库（http://vision.ucsd.edu/～leekc/ExtYaleDatabase/ExtYaleB.html）中 ，有 38个个体。对于每个个体，使用不同光照条件下的14幅图像，并且每个样本具有48×42的分辨率。将每个图像堆叠为矩阵列，称为原始数据O，显然这是一个2 016×532的矩阵。通过损坏原始数据O中的所有样本来构建观察数据X，损坏的像素百分比设为5%，如图4（a）所示。

接着，通过Tri-Decom获得恢复数据D和噪声数据E和F，D中的一些恢复图像在图4（b）中（此时D的秩为52），E中的稀疏噪声图像和F中的稠密噪声图像则在图4（c）和图4（d）中。同样出于可视化的目的，对稠密噪声分量F进行了二值化。作为对比，RPCA的分解结果如图5所示，从图中可以看出，RPCA也可以较好恢复出干净图像。

对于训练集中的样本（例如图4（a）列），损坏的像素占比5%，导致的误差具有稀疏性特点，而由于光照等变化引起的误差具有稠密性特点。这两种噪声的混合对后续识别等任务带来不利影响。本文提出的Tri-Decom非常清楚地对稀疏噪声和稠密噪声进行了分离（图4（c）和图4（d））。这里需要特别指出的是，RPCA的噪声分量E包含了稀疏噪声和稠密噪声（图5（c）），无法明确分离开。

Fig.3 Background modeling from video surveillance图3 监控视频的背景建模

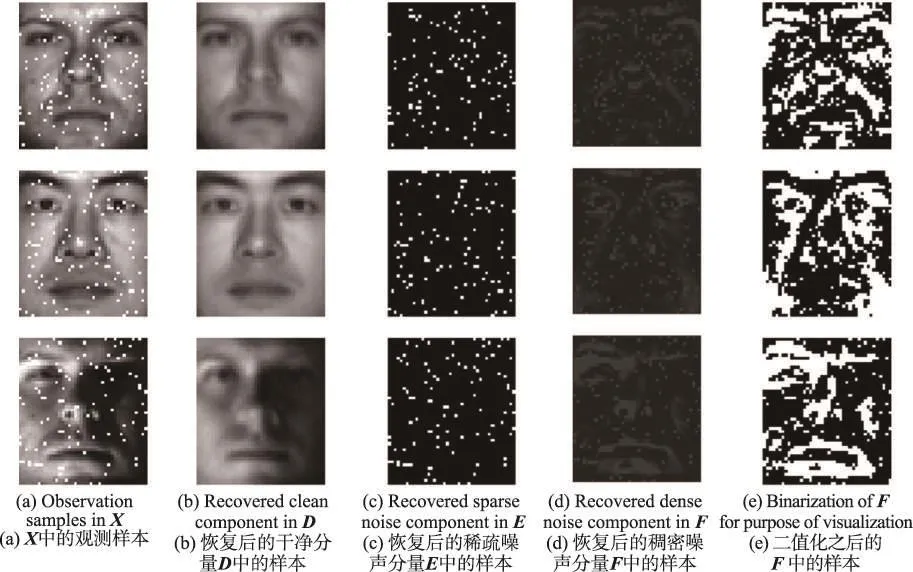
Fig.4 Recovered results by Tri-Decom(λ=0.02,γ=0.09)图4 三分解模型的恢复结果（λ=0.02,γ=0.09）

Fig.5 Recovered results by RPCA(λ=0.014)图5 RPCA的恢复结果（λ=0.014）

Table 2 Running time of different algorithms on Extended Yale B(data size:2 016×532）表2 在Extended Yale B数据集上（数据尺寸:2 016×532）不同算法计算时间 s

最后表2中列出了在Extended Yale B数据集上算法计算时间的比较，由于Tri-Decom优化变量多于RPCA，导致时间略高于RPCA，由于RPCA-Lp求解一个非凸问题，耗时最长，而DNMD迭代中比Tri-Decom更频繁进行奇异值分解，也需要较多时间。

5 结论

针对基于低秩假设在处理图像恢复问题时存在的缺陷，提出了一种新的图像恢复模型Tri-Decom，用于处理同时受到稀疏和稠密噪声破坏的图像数据。所提出的Tri-Decom模型通过乘子交替方向法求解，可以有效地从观测数据中分离干净数据、稀疏噪声和稠密噪声。实验表明该方法能取得比其他算法更好的恢复效果。但如何利用其他噪声度量函数使得算法达到最优效果，比如来自鲁棒统计文献的Huber函数[27]来降低异常值的影响是今后需要重点研究的问题。