贝叶斯稀疏表示高光谱图像超分辨率方法*

黄 伟，许蒙恩，徐国明,3+，黄勤超

1.中国电子科技集团公司 第二十七研究所，郑州 450047

2.中国人民解放军陆军炮兵防空兵学院，合肥 230031

3.安徽新华学院 信息工程学院，合肥 230088

1 引言

高光谱成像技术融合了成像技术与光谱技术，所获得的图像包含丰富的光谱信息、空间信息以及辐射信息，具有光谱连续、图谱合一的特性，能够以较高的光谱信息对地物目标进行精细化解析，增强对地物信息的提取能力[1]。高光谱成像的光谱特性有助于提高许多计算机视觉任务的性能，包括图像追踪[2]，目标识别与分类[3]，在遥感领域也起到重要作用。高光谱传感器在遥感成像中能够实时获取研究对象的空间影像和每个像元的光谱曲线，可在提供地物空间分布信息的同时提供丰富的光谱信息，具有更好的地物检测与分类能力[4]。然而，由于高光谱传感器的空间分辨率限制和地物的复杂多样性，高光谱遥感数据的空间分辨率较低[5]。在目标识别、地物分类、环境变化检测等高光谱遥感的诸多应用中都需要较高空间分辨率的图像，因此有效提升高光谱图像的空间分辨率是十分必要的[6]。为解决该问题，有研究者提出过增大感光元件的物理尺寸，使用高分辨率传感器的简单解决方案，但是进一步降低了到达传感器光子的密度[7]。目前采用基于软件方法的超分辨率（super resolution，SR）技术是提升高光谱图像空间分辨率的有效手段。

为了增强高光谱图像的空间分辨率，通常将高光谱图像与高分辨率的全色图像融合，传统的方法一般是基于投影和替代[8]。但是全色图像缺乏不同波段的光谱信息，重建后的图像会产生光谱信息丢失。Aiazzi等人[9]利用人类视觉对亮度的敏感性，将高分辨率图像的亮度分量与高光谱图像融合，有助于提高图像的空间信息，但是这种方法也会产生图像的光谱失真问题。目前，在基于矩阵分解方法的框架下，将高分辨率的RGB图像与高光谱图像融合提升高光谱图像的分辨率。Kawakami等人[10]用两个矩阵分解因子表示每个图像，并用两个互补因子构建所需的图像。Huang等人[11]利用稀疏矩阵分解方法进行图像融合，在融合过程中使用RGB图像的下采样版本，用于遥感图像的分辨率提升。Wycoff等人[12]通过一种基于交替方向乘子的方法提升光谱图像的空间分辨率，但是该方法需要融合图像之间的空间变换先验知识。Akhtar等人[13]提出一种稀疏空间光谱表示的SR方法，该方法融合高光谱图像与高分辨率的伪彩色图像。该方法的重建性能对算法参数要求较高，比如图像被分解成矩阵的尺寸等问题。Lanaras等人[14]以及Chen等人[15]使用一种光谱解混合的方法对高光谱图像进行SR重建，需要融合图像之间的光谱分辨率彼此接近，另外在光谱高度混合的情况下重建效果较差。

目前，低光谱分辨率成像系统（例如RGB相机）通过场景辐射总体量化获取图像，虽然失去大部分的光谱信息，但是能够保存更多的场景空间信息，空间分辨率远高于高光谱对应物的分辨率[16]。为此，可以考虑将获取的高分辨率图像空间信息与低分辨率的高光谱图像进行融合，提升高光谱图像的空间分辨率。基于该思路，提出一种高光谱图像SR方法，通过非参数贝叶斯稀疏表示将高光谱图像与高分辨率图像融合，联合利用图像的空间结构信息以及高光谱图像的光谱域信息，避免重建图像的光谱失真问题。该方法首先估计场景中材料反射光谱的概率分布以及一组伯努利分布；其次，通过贝叶斯字典学习得到光谱字典，并根据高分辨率图像的频谱量化进行字典变换；然后，利用变换后的字典，通过贝叶斯稀疏编码策略计算高分辨率图像的稀疏编码矩阵；最后，将贝叶斯学习的字典与稀疏编码矩阵联合重建高分辨率的高光谱图像。

2 高光谱图像SR问题模型

高光谱图像SR的目标是从获取的低分辨率高光谱图像Yh和相应的高分辨率图像Y中，恢复得到高分辨率的高光谱图像T，其中Yh∈Rm×n×L，Y∈RM×N×l，T∈RM×N×L，M、m、N和n表示空间维尺寸，L和l表示光谱维数。由于M≫m、N≫n、L≫l，使得方程求解是个欠定问题，现考虑将Yh和Y分别作为目标图像T的线性映射，其形式如下：

ψh表示 RM×N×L→Rm×n×L，ψ表示 RM×N×L→RM×N×l。

由高光谱图像的稀疏性先验信息可知，一幅高光谱图像中通常只包含少数不同的材料，并且与整个图像相比，每个像素中通常只含有非常少量的不同光谱，可以通过线性组合光谱字典Φ的原子来稀疏表示Yh。将Yh的像素连接形成二维矩阵形式，可用如下形式表示：

式（2）中，Φ∈RL×|δ|是一个具有列向量φk的矩阵，φk表示图像中不同材料的反射光谱，其中k∈δ,δ={1,2,…,K}，|·|表示该集合的基数；B∈R|δ|×mn表示系数矩阵。由于一个图像场景中通常仅包含几个不同光谱的材料，因此|δ|≪mn。同理，将Y的像素连接形成二维矩阵形式∈Rl×MN，可得：

式（3）中，∈Rl×|δ|，A∈R|δ|×MN,A表示系数矩阵。

由于图像Yh和Y表示相同场景，可以通过一个变换矩阵γ∈Rl×L进行如下表示：

图像Yh和图像Y中的像素分别包含Φ和的稀疏表示，因为与整个图像相比，一个像素中通常包含非常少的光谱。此外，|δ|的值可以在不同场景之间发生变化，取决于场景中不同光谱的材料数量。下文中，将Φ称之为字典，为变换字典，字典的列被称为字典原子，并且系数矩阵（例如A和B）被称为稀疏编码矩阵或相应图像的稀疏码。

3 超分辨率方法

本文的SR方法可以分为四个主要阶段。首先，通过贝叶斯字典学习框架从高光谱图像中学习得到光谱字典；其次，使用两个输入图像之间的频谱变换矩阵γ得到变换字典，即=γΦ；然后，变换字典对高分辨率图像进行稀疏编码得到A∈R|δ|×MN；最后，利用字典Φ和稀疏编码矩阵A重建图像T，即T=ΦA。

3.1 贝叶斯字典学习

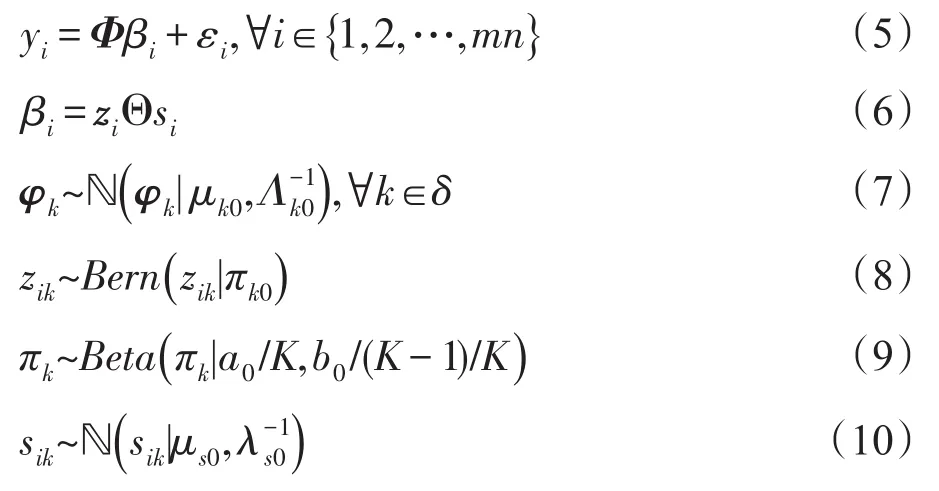
上述模型中，～表示服从于某一分布，式（7）、式（10）和式（11）中ℕ指的是正态分布，式（8）和式（9）中Bern和Beta分别指的是Bernoulli分布和Beta分布；此外，zi∈R|δ|是一个二进制向量，它的第K个分量zik服从Bernoulli分布。Beta先验置于πk上，其中参数为a0和b0。将zi作为支持向量，si∈R|δ|的每个分量sik服从正态分布。

为方便处理，将式（7）字典原子φk的正态分布中的矩阵Λk0约束为λk0IL，IL表示RL×L中的实体，λk0∈R是预设常数。式（7）的正态分布定义在基向量φk上，零向量被用于表示正态分布的均值参数μk0。同理，令Λε0=λε0IL，并且正态分布的均值参数μs0=0，λs0∈R是预设常数。zi∈R|δ|是一个二进制向量，原式（5）中字典的系数被约束为二进制项。为了放松式（5）中字典系数βi的二进制约束，通过非信息性的伽马超先验λs0和λε0，使得：

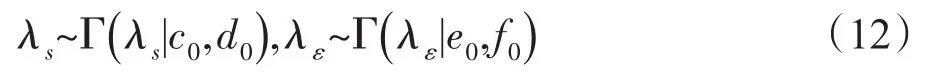
式（12）中，Γ表示伽马分布，c0、d0、e0、f0分别是参数。由此形成的非参数贝叶斯模型是完全共轭的，可以使用Gibbs采样来对其进行贝叶斯处理，得到最终的采样方程（13）。将第k个字典原子φk对yi的贡献表示为：

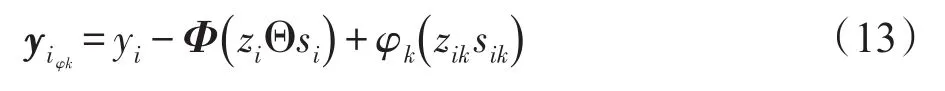
通过以上处理，可以得到用于本方法的Gibbs采样过程的分析表达式[18]：

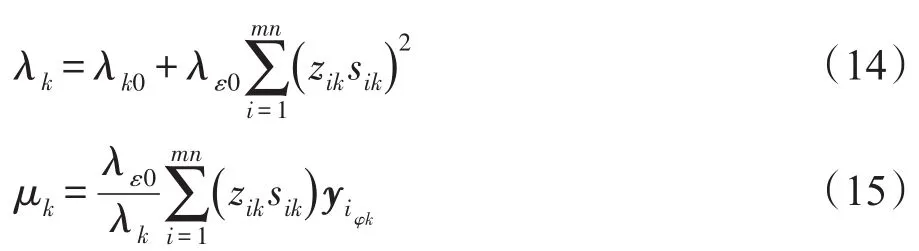
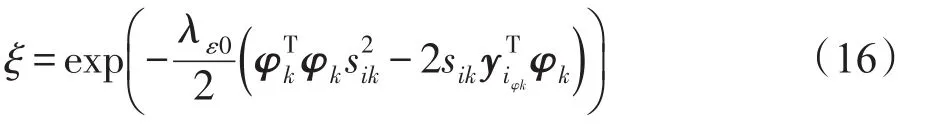
通过上述贝叶斯推理，获得模型参数上的后验分布集，其中一个是字典原子的分布集 ℵ={ℕ(φk|μk,;二是支持指示向量的分布集ℜ={Bern(πk),k∈δ}，ℜ⊂R。Bern(πk)是所有支持指示向量的第k个分量，并且 ∀i∈{1,2,…,mn}，zik～Bern(πk)。通过计算得到字典原子的分布集，从中抽取多个样本并计算它们各自的均值来估计Φ。将字典Φ作为贝叶斯字典学习的最终结果，可以通过=γΦ得到变换字典。

3.2 贝叶斯稀疏编码

通过贝叶斯字典学习方法得到光谱字典Φ，进而得到变化字典，可以用来计算高分辨率图像Y的稀疏编码矩阵，并用所得的稀疏编码矩阵和光谱字典Φ得到目标图像T∈RM×N×L。尽管已经存在一些经典的稀疏编码算法，比如正交匹配追踪算法和基追踪算法，但是当它们与使用Beta过程学习得到的光谱字典Φ一起使用时，重建效果相对较差。为此，采用一种贝叶斯稀疏编码方法，可以与使用Beta过程学习的光谱字典一起使用。

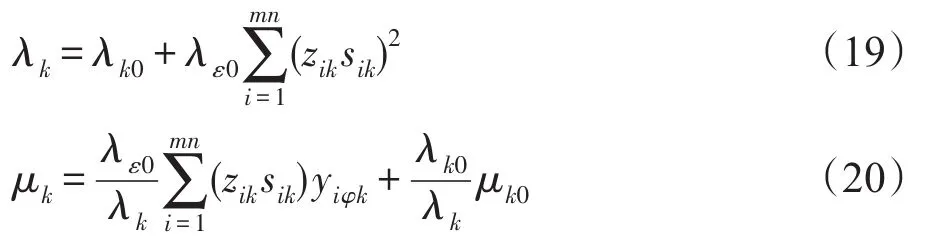
式（19）中，λk0→∞ 指出λk0≈λk；式（20）中，μk0≈μk。意味着可以从该正态分布中获得相同的采样数据，在处理过程中忽略更新字典原子的后验分布，其中第k个后验分布的样本是该矩阵的第k列，贝叶斯稀疏编码可以直接使用变换字典中的原子作为样本。

（2）根据与固定字典原子相关联的伯努利分布，对支持向量zi进行采样。通过支持向量的分量上的分布集={Bern(πk),k∈δ}确定支持向量的分布，使用向量π∈R|δ|，将分布参数存储在集合ℜ中。采样时直接使用π的第k个元素作为πk。将上述处理过程纳入到Gibbs采样，可以在字典上较好地稀疏表示，其中；在均方误差中，稀疏表示y的最佳估计为=是范围算子，分别表示期望值和条件期望算子。令y在字典̇上的稀疏表示系数α的估计值为，可以定义均方误差（mean square error，MSE）为：

在上述采样过程中，执行Q次得到支持向量zq和y的权重向量sq，其中q∈(1,2,…,Q)：

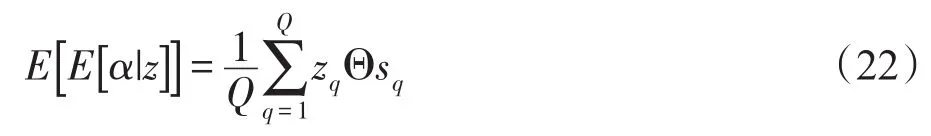
（3）根据以上知识，重复执行Q次，最终计算出稀疏编码矩阵A：

αi作为稀疏编码矩阵A的列向量，其中i∈{1,2,…,MN}。矩阵Zq和Sq分别表示支持矩阵和权重矩阵，。最后使用稀疏编码矩阵A和贝叶斯学习的字典Φ得到高分辨率目标图像T：

3.3 超分辨率算法

根据以上分析，基于贝叶斯稀疏表示的高光谱图像SR算法总结如下：

输入：低分辨率的高光谱图像Yh。

初始化：设定各参数值，a0、b0、c0、d0、e0、f0。

（1）通过贝叶斯字典学习，得到场景材料反射光谱的概率分布和一组伯努利分布Bern(πk)。

（2）通过材料反射光谱学习得到光谱字典Φ，并根据高分辨率图像的频谱量化通过式（4）进行字典变换=γΦ，得到变换字典。

（3）利用变换后的字典，通过式（23）计算高分辨率图像Y的稀疏编码矩阵。

（4）利用光谱字典Φ和稀疏编码矩阵A，通过式（24）得到目标图像T，T=ΦA。

输出：重建的高分辨率目标图像T。

4 实验结果与分析

4.1 实验说明与环境

为了检验本文方法的有效性，实验所采用的图像包括公共数据库（CAVE database）中的标准测试图像以及高光谱成像仪器采集的实际图像，并与双三次插值方法、稀疏编码超分辨率方法[19]（sparse coding super resolution，ScSR）、矩阵因子分解方法[10]（matrix factorization，MF）以及最近提出的耦合光谱解混合方法[14]（coupled spectral unmixing，CSU）等进行比较分析。为了评估本文方法的重建效果，实验结果从主观评价和客观评价两方面进行比较分析。主观评价主要从视觉效果比较图像的去模糊以及细节信息重建等情况，客观评价主要从均方根误差（root mean square error，RMSE）和峰值信噪比（peak signalto-noise ratio，PSNR）进行图像重建的质量比较。另外，还对不同SR方法进行重建效率的对比分析。

本文采集实验图像所用的设备是分孔径同时式高光谱偏振成像仪，处理图像进行实验的运行环境是：Lenovo ideapad700，Intel Core i5-6300HQ，CPU@2.30 GHz，8 GB RAM，MATLAB R2014a。

4.2 实验结果与分析

本文所做的实验包括对CAVE database中的图像、高光谱的“教学楼”图像，以及实际采集得到的“卡车”缩比模型图像的SR重建，实验图像的光谱波段范围是400 nm到700 nm，光谱分辨率为10 nm，共31个光谱波段。实验中对高分辨率参考图像进行高斯模糊以及降采样处理，得到待处理的低空间分辨率图像。高斯模糊核的尺寸为8×8，行和列的降采样因子均为4，稀疏编码阶段Q取31次。分别采用双三次插值方法、ScSR方法、MF方法、CSU方法以及本文方法对低分辨率高光谱图像进行SR重建，并对不同方法的重建效果进行比较。限于篇幅，文中仅展示“教学楼”图像以及“卡车”图像的实验结果。

Fig.1 Reconstruction effect of different SR methods in“building”image图1 “教学楼”图像不同SR方法重建效果

图1比较了“教学楼”图像在不同SR算法的重建效果，由于高光谱图像波段众多，图1所示为540 nm波段的重建图像。图1（a）为待处理的低分辨率图像；如图1（b）所示，双三次插值方法的重建图像整体比较模糊；图1（c）为ScSR方法的重建图像，与双三次插值相比，提高了图像的整体清晰度，但是边缘部分比较平滑；图1（d）为MF方法的重建图像，与双三次插值方法和ScSR方法相比，MF方法提高了图像的整体锐度，但是图像中的车辆仍存在平滑模糊问题；图1（e）为CSU方法的重建图像，CSU方法相比于MF方法提高了图像的锐度及清晰度，比如图像中车辆的轮廓更加清晰，但是图像左下方仍然比较模糊；图1（f）为本文方法的重建图像，与MF方法和CSU方法相比，本文方法更好地提高了图像边缘的锐度及整体清晰度，并且恢复了更多的图像细节信息，包括道路与车辆等。

图2展示了使用不同SR方法对实际采集的“卡车”图像SR重建的结果，所示为620 nm波段的图像。图2（a）为低分辨率的待处理图像；图2（b）为双三次插值方法的重建图像，可以看出图像整体效果仍比较模糊；图2（c）为ScSR方法的重建图像，与双三次插值相比提高了图像的整体清晰度，但是图像中“卡车”以及周围的情况仍然比较平滑；图2（d）为MF方法的重建图像，与ScSR方法相比提高了图像的锐度，但是图像的边缘部分仍存在平滑现象；图2（e）为CSU方法的重建图像，CSU方法相比于MF方法提高了图像的锐度及清晰度，恢复了“卡车”图像上的细节信息，但是车顶的白色字样信息仍不清楚；图2（f）为本文方法的重建图像，与MF方法和CSU方法相比，本文方法更好地提高了图像边缘的锐度以及整体的清晰度，并且较好恢复了“卡车”图像车顶的白色字样信息。

Fig.2 Reconstruction effect of different SR methods in“Truck”image图2 “卡车”图像不同SR方法重建效果

从上述不同SR方法的实验结果可以看出，本文方法相较于其他四种方法，能够较好地恢复低分辨率的高光谱图像信息。为进一步客观评价本文方法的效果，使用均方根误差（RMSE）以及峰值信噪比（PSNR）作为量化评估的度量标准，与其他SR方法进行比较。RMSE越小、PSNR越大，表明高光谱重建图像的质量越高。实验结果如表1所示，其中粗体标记的数值表示相应评价指标下具有最优效果：

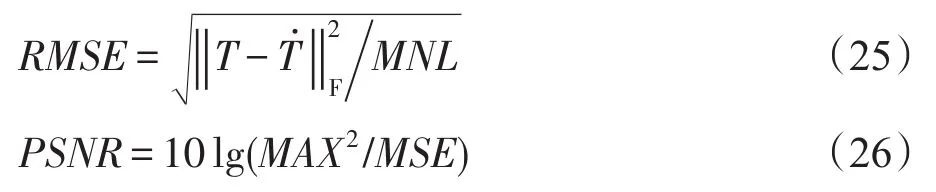
式（25）中，T和̇分别表示真实图像和重建后恢复的图像，M和N分别表示高光谱图像的空间维尺寸，L表示光谱维数。式（26）中，MSE=RMSE2，MAX表示̇的最大值。测试图像如图3所示，包括CAVE database中的“图画”“辣椒”“人脸”“格子”“教学楼”等图像，以及实际采集得到的“卡车”图像。

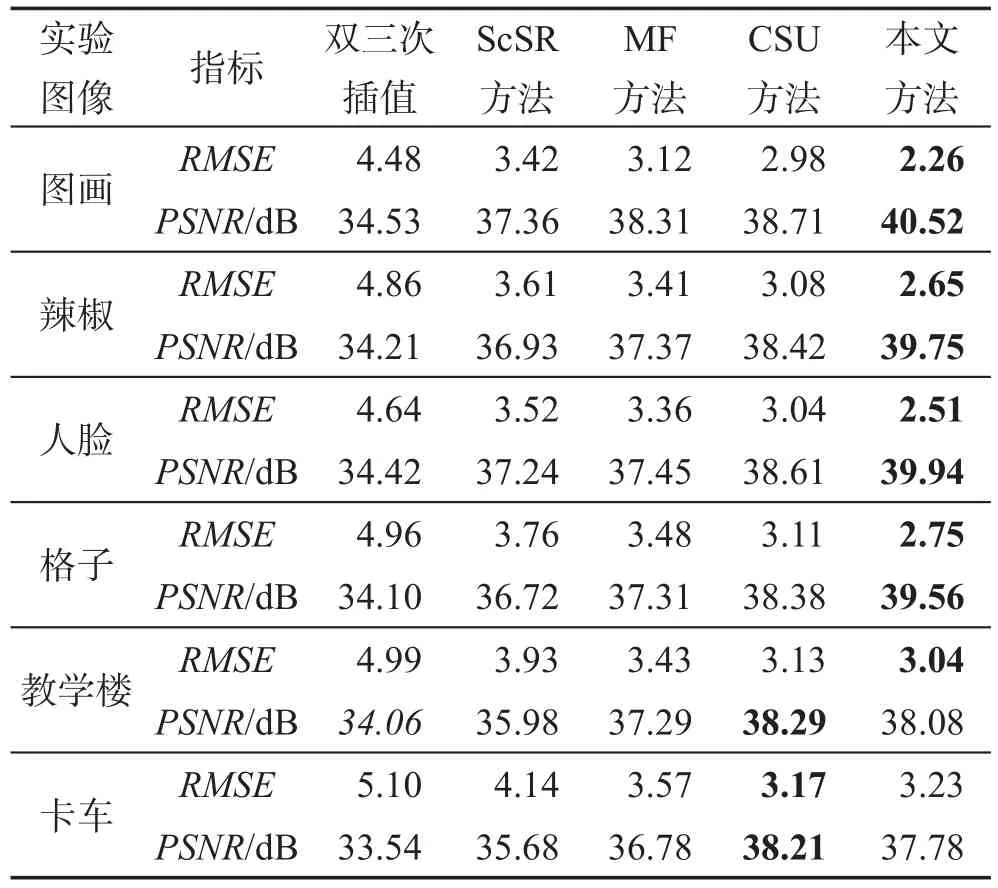
Table 1 RMSE andPSNRof different SR methods表1 不同SR方法的RMSE和PSNR

Fig.3 Test images图3 测试图像

从表1中不同SR方法的RMSE和PSNR值可以看出：本文方法比双三次插值方法、ScSR方法、MF方法以及CSU方法重建的图像具有更小的均方根误差，更大的峰值信噪比，图像重建精度更高。

表2是不同SR方法之间的运算时间对比结果。从表2可以看出双三次插值方法的运算时间最快，但是其图像重建效果比较差。本文方法的运算时间略高于ScSR方法和CSU方法，主要是在稀疏编码阶段对不同光谱波段的图像进行多次处理。综合考虑不同SR方法的重建效果以及运算效率，本文方法具有更好的重建效果，运算效率略高于相似的稀疏表示经典方法，而这也是本课题下一步要研究的内容。

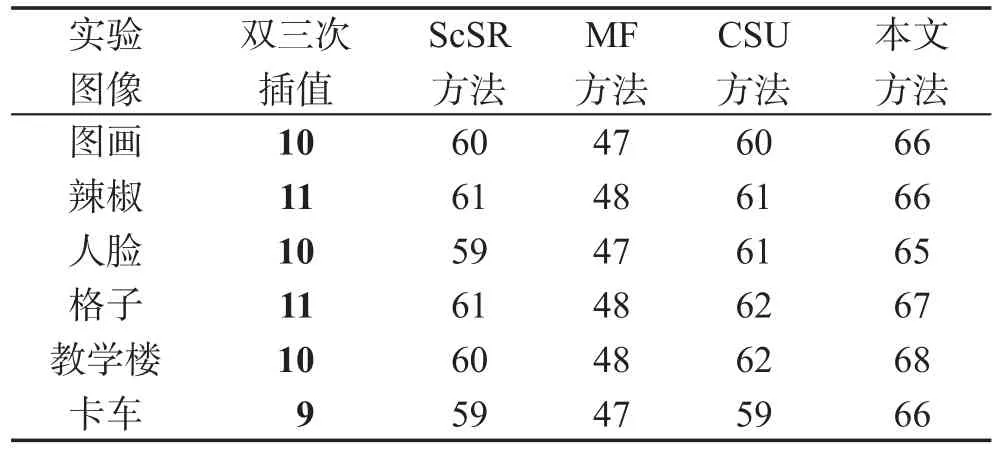
Table 2 Computing time of different SR methods表2 不同SR方法的运算时间 s

5 结束语

针对所获取的高光谱图像空间分辨率较低的问题，通过对高光谱图像超分辨率方法进行研究，提出一种贝叶斯稀疏表示的方法。将高分辨率图像的空间结构信息与低分辨率的高光谱图像进行融合，提高高光谱图像的空间分辨率。本文方法能够联合利用图像的空间结构信息以及高光谱图像的光谱域信息，避免了传统稀疏编码方法重建图像的光谱失真问题。通过与传统的超分辨率方法、稀疏表示的经典方法、基于矩阵分解的方法以及最近提出的耦合光谱解混合方法进行实验对比，检验本文方法的重建效果。实验结果分析表明，本文方法在主观视觉方面，图像的细节信息更加清晰，客观指标上RMSE和PSNR的值也优于其他SR方法，证明本文方法能够有效提升高光谱图像的空间分辨率。