数据点的密度引力聚类新算法*

温晓芳，杨志翀，陈 梅

兰州交通大学 电子与信息工程学院，兰州 730070

1 引言

随着互联网和信息产业的高速发展，数据量不断增长，形式也呈现多样化、复杂化。但传统的数据处理技术仍处于贫乏的状态[1]。如何有效地识别各种数据集的真实结构是数据挖掘目前面临的一个主要问题。聚类分析作为数据挖掘的一项重要技术[2]，能够根据数据间的相似性识别出数据集中的内在模式，特别适用于探索数据点之间的相互关系，以对其结构进行评估[3]。然而，很多先进的聚类算法在划分不同类型的数据集时，均遇到了精确性不高或者执行效率较低等问题[4]，因此聚类算法性能的提高势在必行。

目前，已有许多聚类算法被提出。其中，最经典的基于划分的方法有k-means和k-medoids，但是由于这两种算法对初始中心的选取较为依赖，通常不能获得全局最优结果，并且只能发现球状簇。基于密度的一个经典聚类算法DBSCAN（density-based spatial clustering of application with noise）[5]将高密度点连通区域划分为簇，它能够识别任意形状和任意大小簇，但当数据集的密度变化较大时，聚类质量就会变差。OPTICS[6]通常被认为是DBSCAN的改进算法，它不显示产生的结果簇，而是为聚类分析方便生成了一个有序的对象列表，但其依然对数据集中的密度变化较敏感。一个先进的层次聚类方法——CHAMELEON[7]使用动态模型通过簇间相对互连度和相对接近度将分开的小簇合并，直到最终簇形成。该算法虽然可以发现任意形状簇，但其时间复杂度非常高。CURE[8]和ROCK[9]也是基于层次的聚类算法。CURE使用多个点表示簇，并使用随机抽样的方法来提高效率，从而可以有效处理大数据，并且能检测到异常点，但其时间复杂度依然较高。相对于CURE，ROCK克服了其缺点，但它对全局参数非常敏感，不能识别密度不均匀的数据集。AP（affinity propagation）[10]是一个根据数据点间相似度自动聚类的方法。吸引度和归属度信息在数据点间迭代交换，直到高质量的一组样本和相应的簇出现。该算法不需要用户指定聚类个数，但需事先设置参考度，且数据量大时运行时间长。

近年来，人们又提出了一些新的聚类方法。Attractor[11]是一个社团检测聚类算法。它通过检测节点之间的“距离”变化，使得相同社区的节点互相靠近，不同社区的节点彼此远离，自动在网络中发现社区。为分析网络中的社团结构提供了一种直观的方法。CLUB（clustering based on backbone）[12]是一个根据簇的密度主干聚类的算法。它先将两个互k-近邻点聚在一起形成初始簇，然后取初始簇内密度较大的半数点，不断吸引与其有k-近邻关系的点来扩展簇；最后将剩余不含标签的点分配给密度比它大的最近邻所属的簇，形成最终簇。该算法能自动适应不同密度，并正确检测出簇的数目和结构，为发现任意簇提供了有价值的参考。一个无参聚类算法Txmeans[13]采用自顶向下分而治之的策略，迭代地将一个簇分成两个不相交的子簇。其性能在噪声和变化的聚类结构上表现稳定，并且可扩展到大型数据集，为层次聚类提供了一种新的思路。Perch[14]是一个非贪心增量算法。它先将新数据点路由到生长树的树叶，然后通过旋转操作来保持其质量，最后以递增的方式在数据点上构建树结构。这种树结构使得有效搜索大数据集成为可能，同时为提取不同分辨率下的多个簇提供了丰富的数据结构。

基于上述存在的问题，本文提出一种数据点间的密度引力聚类算法。从物理学角度来看，任何两个物体间存在着万有引力。由于数据集中的每个点可以看作为物体的质点，从而认为两个数据点间也存在着某种引力。本文研究将这种引力与数据点的密度建立起一种关系，称之为密度引力。通过此引力将每个数据点与密度比它大且距离其最近的互近邻点划分到一起形成初始簇。然后合并具有共同点的初始簇，得到数据集的真实划分。该算法可以发现任意簇，如实地反映了数据的实际情况。

本文其余部分安排如下：第2章描述了数据点的密度引力聚类算法；第3章分析比较了本文算法与对比算法在不同数据集上的实验结果；第4章对本文进行总结和未来展望。

2 密度引力聚类算法

从物理学角度来看，任何两个物体在自然界中是相互吸引的。数据集中的每个点可以看作为一个质点。通过模拟事物在自然界中的运行规律和自然状态，本文定义了密度引力的概念。进一步，提出基于数据点的密度引力聚类算法。

设在欧式空间中，存在一个包含n个数据点的数据集D，记作D={x1,x2,…,xi,…,xn}，i=1,2,…,n。其中，xi表示数据集D中的第i个点，并且每个点都有p个属性，属性之间相互独立，每个点可以表示为xi=(xi1,xi2,…,xip)。

2.1 相关定义

定义1（k-近邻）对于D中的每个点xi，通过计算xi与D中其他点之间的欧氏距离并按从小到大的顺序排列，其中排在前k个的点均被称为xi的k-近邻。记作Nk(xi)，且Nk(xi)⊂D。

定义2（互k-近邻）设数据集D中，如果点xi是xj的k-近邻点，同时xj也是xi的k-近邻点，则称xi和xj互为k-近邻；否则，二者不互为k-近邻。另外，xi所有的互k-近邻记作MNk(xi)。

定义3（点密度）数据集中点的局部密度与其周围邻居点的密集程度有关。若点xi的邻居越多，邻居距离该点越近，则点xi的密度就越大。因此定义点密度与其邻居的个数成正比，与邻居点到该点间的距离和成反比。点密度如式（1）所示：

其中，ρi表示点xi的密度，K表示xi邻居点的个数，dij表示xi与其邻居xj之间的欧氏距离。

定义4（密度引力）自然界中任意两个物体之间存在着引力，当把物体看作为质点时，根据分布规律，本文提出两质点之间仍存在一种引力——密度引力。如式（2）所示：

其中，F表示点xi和xj之间的密度引力，G表示一个引力常量。

本文使用基于互k-近邻的距离度量，弥补了单方向挖掘数据点而缺乏的信息，使得数据点之间的关系更加紧凑。采用这种方法可以将相关性强的点吸引进同一个簇，实现数据集的真实划分。

2.2 聚类过程

本文提出的密度引力聚类算法将通过三个阶段来发现数据集中的真实簇。首先，通过式（1）获得每个点的密度并寻找其互k-近邻；然后，采用密度引力的思想形成初始簇；最后，将具有共同点的初始簇合并形成最终簇。具体过程如下描述。

算法1获得点密度及其互近邻

输入：数据集D，最近邻居个数k。

输出：每个点的密度ρi，互近邻集合M。

在第一阶段，首先通过式（1）计算每个点的密度ρi。当分子K依次增加1时，分母依次增加一个距离diK且diK≥diK-1，因此整体点密度随着K的增大而减小。然而每个点密度的相对大小几乎保持不变。为了方便计算，将K设置为固定值5。然后，寻找D中每个点的互k-近邻点（k≥K）。对于每个点xi，找到其k-近邻后，依次判断是否同时满足条件xj∈Nk(xi)和xi∈Nk(xj)，如果满足，那么xi和xj为互k-近邻；否则，扫描下一个点，直到所有的点都被扫描完。最后，将点xi和其互k-近邻放入mi中，再将所有的mi放入互近邻集合M中。

在第二阶段，数据集中的每个点有三种情况：（1）没有互k-近邻。说明点xi周围比较稀疏，成为孤立点的概率比较大，将该点独自放在一个簇中。（2）点xi的密度大于其所有的互k-近邻点的密度。说明点xi周围的点比较密集，很有可能是簇的代表中心点，且对每个互k-近邻点的吸引比较大，从而将其与所有的互k-近邻点聚集到同一个簇中。（3）点xi的密度小于或等于其所有的互k-近邻点的密度。说明点xi的互近邻中有比其密度大的点，同时对xi具有很强的吸引力，将点xi分配给密度比它大且距离最近的互k-近邻点形成初始簇，其中也包含密度相同的点。通过这种分配方式可以将密集的数据点划分到同一个簇，稀疏的点相隔开，过于分散的点则被识别为异常点。

算法2形成初始簇。

输入：每个点的密度ρi，互近邻集合M。

输出：初始簇集合C。

算法3合并得到最终簇

输入：初始簇集合C。

输出：最终簇集合C′。

在第三阶段，合并初始簇形成最终簇。上阶段得到的初始簇都是一些比较小的簇集合，由于每个簇中的点相对密集，因此需要将多个具有相同数据点的初始簇合并，逐渐扩大簇的规模，直到没有可以合并的簇为止，最终形成真实的数据结构。采用这种方法不需要用户输入停止参数，可以根据数据集的特点进行自动合并并停止。

2.3 时间复杂度分析

由于该算法使用k-d树[15]作为数据结构，当有效地检索特定点给定距离内的所有点时，时间复杂度为O(nlbn)，其中，n为数据集D中点的个数。在第一阶段中，计算每个点的k个邻居时需要花费O(nlbn)的时间，寻找每个点的互k-近邻时的时间复杂度为O(kn)，其中，k为最近邻居点的数量，由于k≪n，因此寻找互k-近邻的时间复杂度接近O(n)。第二阶段形成初始簇时，外循环中，由于依次扫描数据集中每个点，时间复杂度为O(n)；内循环中，依次扫描每个点的互近邻并进行判断，由于每个点的互近邻个数不尽相等且远小于n，因此时间复杂度为O(mn)，m为所有互近邻的平均数且m≤k≪n，从而此阶段的时间复杂度接近O(n)。第三阶段，合并具有相同点的初始簇平均时间复杂度为O(nlbn)。因此，最后整个算法的时间复杂度计算为O(nlbn)。

3 实验结果分析

为了评估算法性能，将本文提出的算法与六种对比算法分别在六个数据集上进行测试。其中，k-means（http://scikit-learn.org/stable/）、DBSCAN（http://scikitlearn.org/stable/）和 OPTICS（https://github.com/）是三种经典算法；BOOL（binary coding oriented clustering）[16]、CLASP（towards effective and efficient mining of arbitrary shaped clusters）[17]和 CFDP（clustering by fast search and find of density peaks）[18]是三种新算法，代码均由其作者提供。六个数据集分别为：三个二维数据集（Aggregation、Spiral、R15，https://cs.joensuu.fi/sipu/datasets/）和三个多维数据集（Ecoli、Glass、Iris，http://archive.ics.uci.edu/ml/datasets.html）。

同时使用ARI（adjusted rand index）和NMI（normalized mutual information）作为算法的评价指标。它们的取值越大代表结果越接近真实情况。其中，用作比较的结果都是算法在数据集上的最优取值，输入参数通过迭代调整得到，具体分析如下。

3.1 对比算法分析

六种对比算法中的三种经典算法已在引言中做过介绍，本节将对BOOL、CLASP和CFDP三种新算法进行分析。

BOOL是一个多变量数据聚类算法。它首先将所有数据点离散化，并用二进制数字表示；然后使用定义的函数迭代地将所有的小簇合并，形成最终簇。尽管该算法对参数不敏感，且比一些算法更快，但在一些数据集上仍不能获得正确划分。

CLASP首先通过删除异常值来自动缩小数据集的大小，使用k-means算法找到代表点来有效保持簇的形状信息。然后，调整代表点的位置以提高它们的内在关系，使得每个代表点更接近其邻居同时远离其他点。最后它在基于互k-近邻相似性度量下执行凝聚聚类来识别簇结构。不过，运行时需要过多的参数，而这些参数都不太容易确定[3]。

CFDP的核心思想在于聚类中心的刻画，聚类中心同时具有以下特点：簇中心的密度大，由一些局部密度比较低的点围绕，并且这些点距离其他高局部密度点的距离比较大。该算法使得簇的数量直观出现，离群值不论形状和维度被自动发现。然而，需要计算所有的点与点之间的距离，如果样本太大，整个距离矩阵的内存开销特别大。

3.2 算法难点与创新点分析

本文算法特点在于通过将数据点分配给距离其最近且密度比它大的互近邻点来形成初始簇，从而可以自动识别数据集中任意簇。在对比算法中，kmeans将事先随机确定的每个簇中心点看作为初始簇，然后就近分配其他点，导致算法对初始簇具有一定的依赖性；CLASP同样采用k-means找到簇中心并不断调整形成初始簇，使得其最终簇与初始簇的形成紧密相关；BOOL则通过将数据点离散化后用二进制数字表示来形成初始簇，使得空间相对位置较近的数据点聚在一起。由于本文算法是根据数据点密度将每个点分配给其最紧密的互近邻点形成初始簇，从而总是将关系最近的数据点聚在一起，使得算法整个过程对初始簇的形成没有依赖性。

3.3 二维数据集实验分析

表1描述了本文算法与六种对比算法在二维数据集上的实验结果，其中包含了算法最优结果的参数值、ARI和NMI值。参数中k为最近邻居的个数，m为簇的数目。DBSCAN的两个参数分别表示邻居半径和最小邻居数；BOOL的三个参数分别为簇个数的下界、距离参数、异常点参数；CLASP的五个参数分别表示簇个数、最近邻居数、数据集尺寸的调整参数、降维标志和迭代最大次数。从表中清楚地看出，本文算法聚类结果与CFDP一样优于其他算法，评价指标值高达0.99以上，更符合真实情况。

3.3.1 Aggregation数据集上的实验分析

图1展示了本文算法与六种对比算法在Aggregation数据集上的结果。此数据集的特征是簇内密度比较均匀，簇间密度差异不大，且簇的形状是任意的。其中图1（a）是Aggregation的真实情况，图1（b）～图1（h）是各种算法的聚类结果。

显然地，CFDP可以正确地识别出整个数据集的真实簇。其次，本文算法通过使用数据点间密度关系在互近邻中聚类使得相同簇中的点相互吸引，不同簇中的点自然分开，从而能够发现任意形状的簇，与真实结果最接近，仅仅相差三个点。k-means由于受初始簇中心的影响，导致最终的数据结构被硬性分成七个簇，每个簇都是围绕其中心点的一个球状簇，从而没能将该数据集的特征很好地体现出来。同理CLASP对最终的识别也不是很好。DBSCAN由于受密度参数影响，一部分簇边缘的点被错误划分。作为DBSCAN的优化算法，OPTICS结果有所改善，但仍有少数点无法被正确识别。同样地，BOOL则将同一个簇中的部分点视为异常点，最终导致划分不够精确。

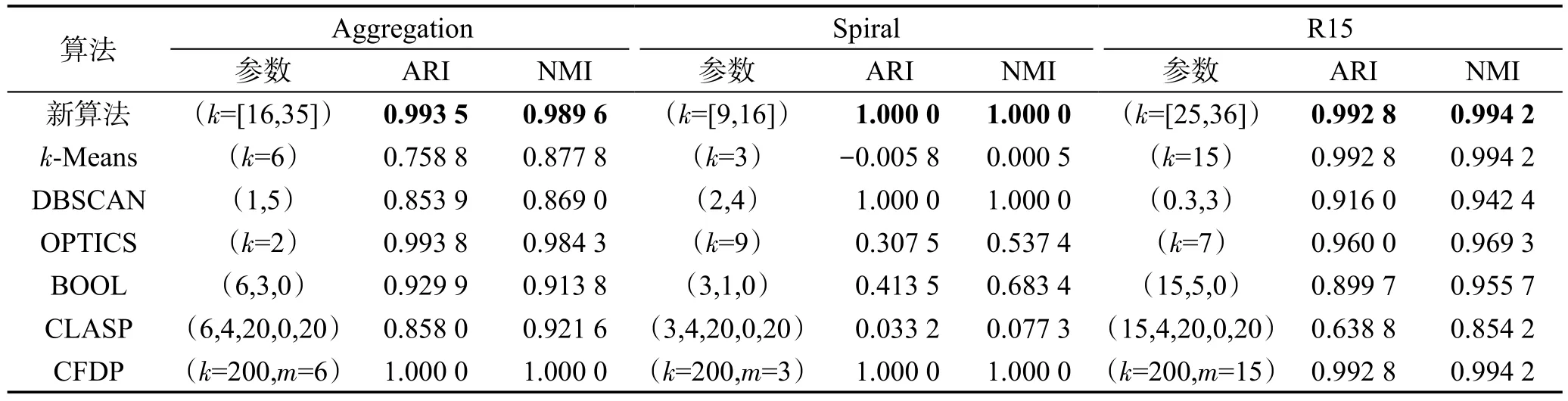
Table 1 Comparison results on 2-dimensional data sets表1 二维数据集上的对比结果

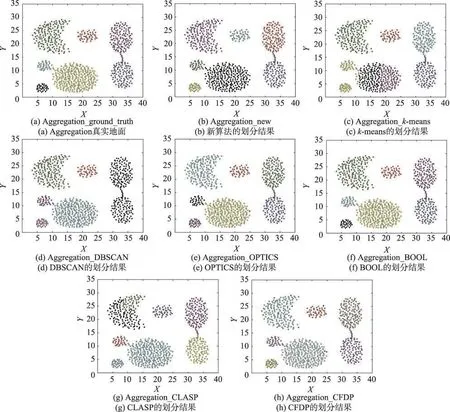
Fig.1 Comparison results on data setAggregation图1 Aggregation数据集上的比对结果图

3.3.2 Spiral数据集上的实验分析

图2展示了数据集Spiral上本文算法与六种对比算法的聚类结果。此数据集的形状是螺旋型，且每个簇内数据点的密度由里到外逐渐变小，簇间距离相似。其中图2（a）是 Spiral的真实情况，图2（b）～图2（h）是各种算法的最优结果。

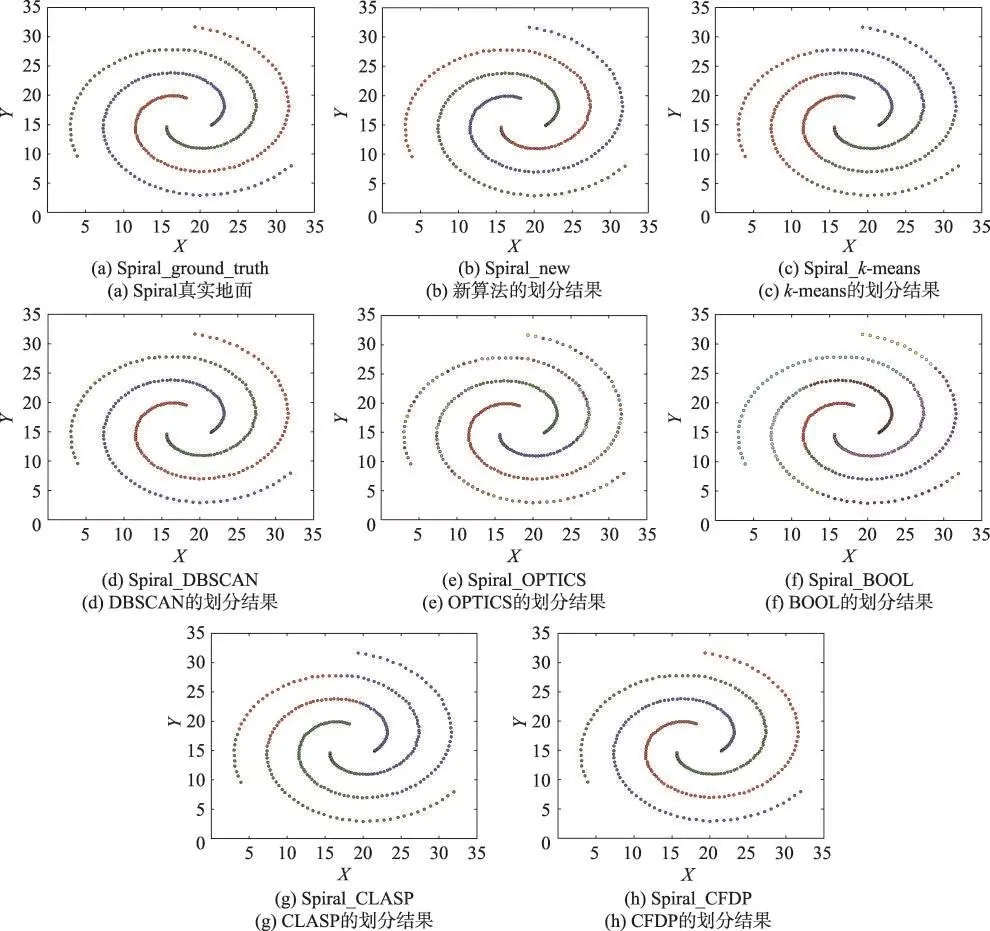
Fig.2 Comparison results on data set Spiral图2 Spiral数据集上的比对结果图

从图2可以清楚地看出，本文算法的聚类结果与DBSCAN和CFDP一样完全符合数据集真实情况。算法同时考虑密度与距离，使得数据集中各个簇自动发现，然后通过相同点串联的方式实现数据集的真实划分。除此之外，其他算法聚类结果均不是很理想。k-means和CLASP一样，受初始簇中心选取的影响，没有考虑到密度，只是将整个数据集平均分成了三部分，导致大部分点被错误划分。OPTICS由于受密度差异影响，密度较大的点实现了正确划分，而其他密度较小的点均被视为异常点。最后，BOOL则根据数据点的位置将整个数据集划分成多个不同的小簇，合并后仍没有很好地将真实簇识别出。

3.3.3 R15数据集上的实验分析

图3显示了本文算法与六种对比算法在数据集R15上的聚类结果。该数据集的特点是每个簇内密度不均匀，簇间距离各有不同，且均为球状簇。其中图3（a）是R15的真实情况，图3（b）～图3（h）是各种算法的最优结果。

不难看出，本文算法与k-means、CFDP一样可以发现数据集的真实结构，性能优于其他几种对比算法。通过对密度和距离的双重考虑，本文算法不仅可以很好地发现任意形状簇，还可以发现球状簇。其次，DBSCAN受簇内密度差异影响，将每个簇中密度较小的点划分为同一个簇，导致簇中部分点被错误划分。相似地，OPTICS则将同一个簇中密度相对较小的点错误地识别为异常点。同样，BOOL和CLASP也没能很好地检测出真实簇。

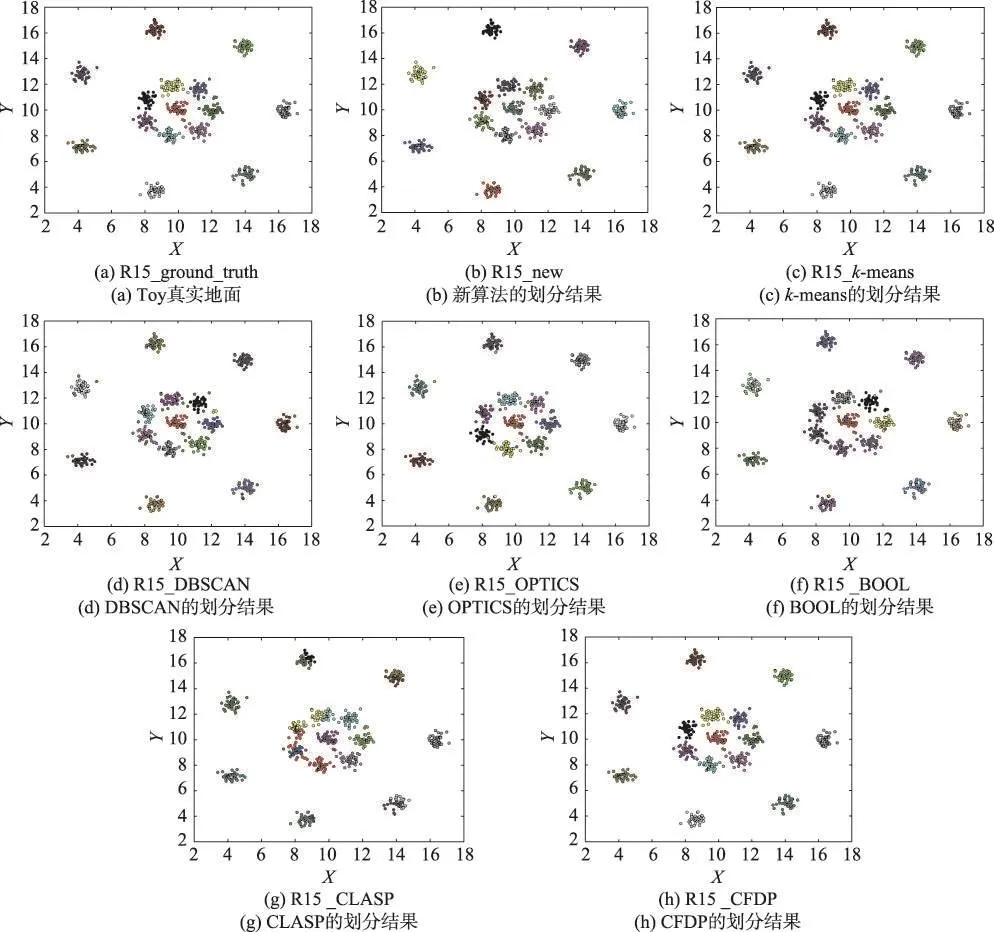
Fig.3 Comparison results on data set R15图3 R15数据集上的比对结果图

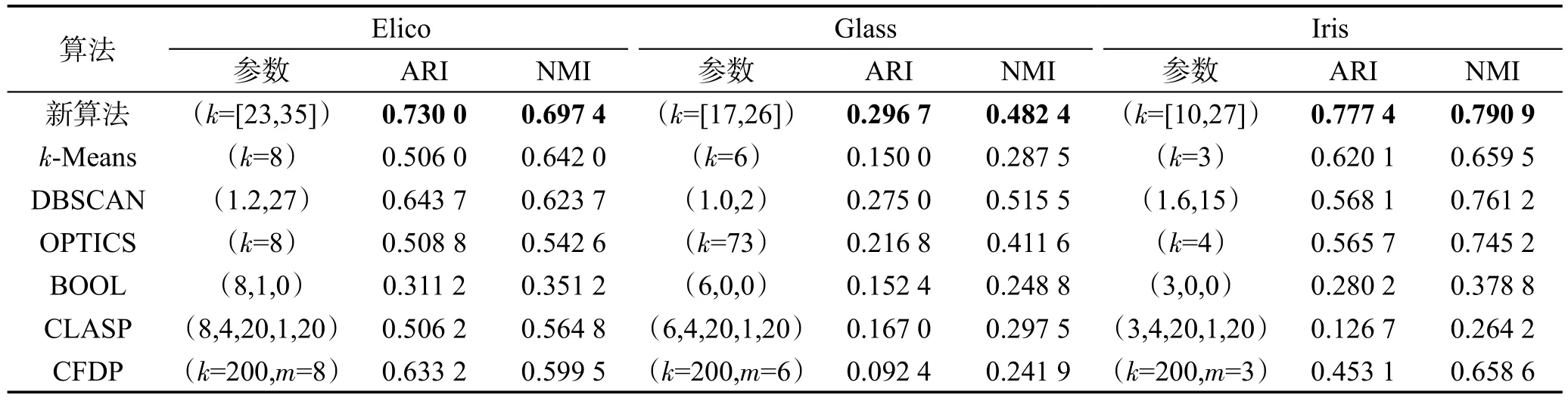
Table 2 Comparison results on multi-dimensional data sets表2 多维数据集上的对比结果

3.4 多维数据集实验分析

表2描述了本文算法与六种对比算法在数据集Ecoli、Glass和Iris上的聚类结果。Ecoli数据集用于预测细胞蛋白质定位位点，七个属性分别为Mc-Geoch信号序列识别方法、von Heijne信号序列识别方法、von Heijne信号肽酶II共有序列评分、预测的脂蛋白的N-末端存在电荷、外膜和周质蛋白的氨基酸含量的判别分析得分、ALOM膜跨越区域预测程序的评分和从序列中排除可能的可切割信号区域之后的ALOM程序得分。Glass是对玻璃种类进行分类的数据集，九个属性包括折射率、钠、镁、铝、硅、钾、钙、钡和铁含量。Iris描述了鸢尾植物类，四个属性分别为：萼片长度、萼片宽度、花瓣长度和花瓣宽度。明显地，在二维数据集上CFDP的聚类性能与本文算法相当，在多维数据集上，本文算法的聚类结果评价指标均高于其他算法，说明其能更好地发现数据集中真实情况。

最后，将七种算法在六个数据集上的评价指标结果值用箱线图直观地表示，如图4、图5所示。二者分别描述了每种算法的六个ARI和NNI统计值的对比情况。其中，每个箱形有以下特征，分别为：箱体上下边界位置对应数据的上下四分位数（Q3和Q1）；箱内的虚线段为中位线位置，表示六个指标值的中位数；箱体最上方和最下方的实线称为内限，分别表示数据的最大和最小非异常值；+表示异常值。

从图4、图5可以看出，本文算法对应的箱线图中各条线段所处位置（包含异常点）几乎都高于其他算法对应的箱线图，说明该算法的聚类性能优于其他对比算法。综上所述，新算法采用互近邻的方法使关系紧凑的点聚集到一起，同时使用密度引力的思想在不论维度和形状的情况下自动发现任意簇，算法整体具有鲁棒性。

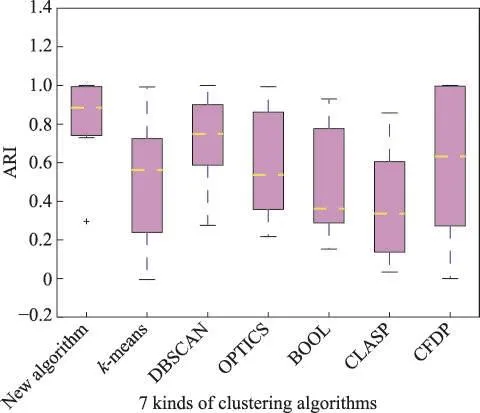
Fig.4 ARI comparison result of 7 kinds of algorithms图4 7种算法聚类ARI值的对比图

4 结束语

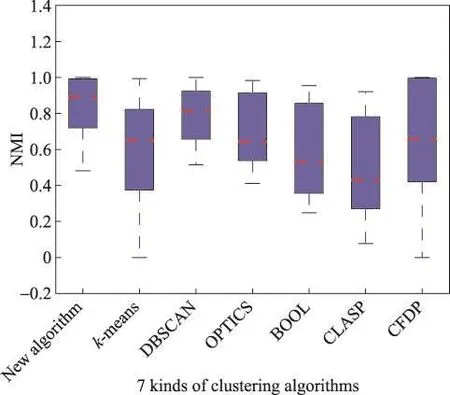
Fig.5 NMI comparison result of 7 kinds of algorithms图5 7种算法聚类NMI值的对比图

为了解决聚类中精确性不高、执行效率低等问题，本文提出了一个基于数据点的密度引力聚类算法。该算法根据数据点的分布情况定义了密度引力的概念，通过密度引力使得自动发现数据集中真实簇。为验证算法的高效性，使用六种先进算法在六种不同维度和类型的数据集上与新算法进行对比实验，结果发现本文提出的新算法在性能上优于其他算法。在未来的研究中，拟尝试研究出更多高效的算法以便于聚类分析。