卷积神经网络中的自适应加权池化

赵长乐，何利力

（浙江理工大学信息学院，浙江 杭州 310018）

0 引言

随着卷积神经网络（Convolutional Neural Network，CNN）在计算机视觉领域的广泛应用，各种不同功能的网络结构被融合到CNN 中。图像分类是计算机视觉中最基础的任务，其数据集庞大规范，输出结果简洁明了，可以很好地评判网络结构的性能优劣［1］。现有CNN 体系结构大多利用下采样（池化）层减小隐藏层中特征图的尺寸，通过池化层可以获得更大的感受野和更少的内存消耗。目前广泛使用的最大池化、平均池化、跨步卷积（使用步幅大于1的滑动窗口）通过在滑动窗口中采用不同下采样策略得到池化结果。例如，LeNet-5［2］将下采样层作为CNN 中的基本层，通过在滑动窗口中对特征值进行求和以降低图像的空间分辨率；VGG［3］、GoogleNet［4］和DenseNet［5］使用平均池化或最大池化作为下采样层；ResNet［6］采用跨步卷积作为下采样层；全局平均池化［7］、ROI pooling［8］和ROI align［9］将任意大小的特征图缩放为固定大小，从而使网络能够适配不同大小的输入。

在CNN 广泛应用前，已有一些关于池化方法的研究。例如，Boureau 等［10］比较了传统方法中平均池化和最大池化的性能，并证实在特征较稀疏的情况下，最大池化相较平均池化可以保留更多判别特征，效果更好；Wang 等［11］、Xie 等［12］研究结果表明，对于一个给定的分类问题，最优池化类型可能既不是最大池化也不是平均池化，而是介于两者之间的某个类型池化。这一结论说明学习池化策略十分必要，本文便是遵循这一研究思路，得到的结果进一步支持了该结论。

1 相关研究

池化的最新研究集中在如何通过新的池化层更好地缩小CNN 中的特征图方面。例如，Fractional max-pooling［13］和S3pool［14］对池化空间变换的方式进行了改进；Mixed pooling［15］和Hybrid pooling［16］使用最大池化和平均池化的组合形式执行下采样；Lp pooling［17］以Lp 范数的方式组合特征值，可将其视为由p 控制的最大池化和平均池化之间的结合体。以上方法可以结合最大池化和平均池化进一步提高网络性能，但也只是简单地基于平均池化、最大池化或它们的组合学习更好的下采样方式，不具有普适性。基于此，Saeedan 等［18］提出细节保留池化法（Detail-Preserving Pooling，DPP），认为图像中的细节应该被保留，冗余的特征可以被丢弃。DPP的细节保留准则是计算滑动窗口中像素的统计偏差，是一种启发式方法，可能不是最优的；Zhu 等［19］提出的Weighted pooling 将信息熵理论与池化相结合，通过分析特征图上的每个特征值得到输入与输出特征图各处的互信息大小，以每个滑动窗口中包含信息量最大的点作为池化结果。该池化方式同样是手工制作，且结果受计算精度影响，并不一定是最优池化结果。

本文将池化操作视为对特征值的加权求和，不同池化策略对应不同大小的权重。在下采样过程中，并非池化区域中所有像素的贡献都相等，某些特征比池化窗口中的其他特征更具区分性，且对于不同的识别任务，区分性大的像素点也可能不同。如图1（彩图扫OSID 码可见，下同）所示，对于同一幅图片，若任务目标为识别花的种类，则红色代表更大的区分性，应被给予更大权重；若任务目标为识别天气状况，则蓝色代表更大的区分性，应被给予更大权重。因此，应根据任务类型不同使用不同的池化策略，在每个池化窗口中对各像素分配与其区分能力大小相对应的权重。传统池化方法在池化窗口内对权重的分配方式固定不变，针对不同类型任务无法做到将细节都妥善保存，若使用不恰当的下采样策略会使模型性能降低。本文提出的自适应加权池化方法给予每个池化层一组权重参数，这些权重参数可使网络根据不同任务类型自行变换池化策略，通过最小化损失函数的方式选取最优池化方法。

Fig.1 Different downsampling strategies under different tasks图1 不同任务下的不同下采样策略

2 池化策略的权重分析

为分析现有下采样方式存在的问题并加以改进，从加权求和的角度出发提出一个用于下采样层的统一函数表达式。具体来说，对给定输入特征图I，经池化后得到输出特征图O，对应的下采样过程可以表述为：将I中左下坐标为(x1,y1)，右上坐标为(x2,y2)的滑动窗口映射到O中输出位置为(x0,y0)处，用函数表示为：

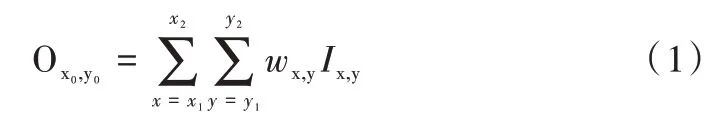
式中，Ix,y为输入特征图(x,y)处的特征值；Ox0,y0为输出特征图(x0,y0)处的特征值；wx,y为权重参数，表示(x,y)处特征值在池化时被分配的权重大小。对于2×2 大小，步长为2的滑动窗口而言，x2-x1=2，y2-y1=2，x1=2x0，且为使权重参数之和为1的性质在式中得以体现，可将其表示为：

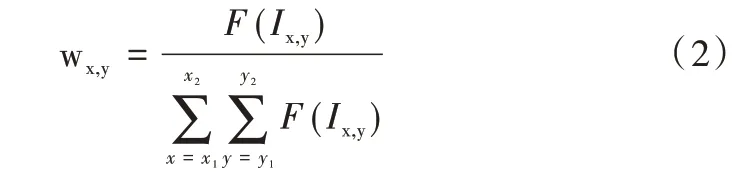
式中，F(·)称为重要性函数，作用在滑动窗口中的每个特征值上，得到的函数值反映了I中对应位置特征对于该任务的区分性大小，且F(x) ≥0。因此，可将池化过程函数表示为：

该函数将池化过程分为两个步骤：首先对滑动窗口中各特征值的重要性进行归一化得到权重，然后根据权重大小对特征值进行加权求和得到池化结果。

由于池化过程本质上是有损的，其将大的输入压缩成小的输出，因此有必要仔细考虑如何对一个滑动窗口中的特征值进行权重分配。为此，本文通过该函数分析一些广泛使用的下采样方式，并据此提出理想池化的特性。图2为在加权求和角度下的一些下采样方法。

2.1 最大池化和平均池化

给定F(x)=exp(βx)，β=0 表示平均池化，β→∞表示最大池化。平均池化在一个池化窗口中给所有位置的特征值赋予了相同的重要性，最大池化将所有注意力放在池化窗口中的最大特征值上，这两种池化方式都不是最优的。基于对特征重要性在局部范围内相等的强假设，平均池化损害了有区分性但是面积较小的特征，导致下采样特征模糊。最大池化假设池化窗口中最大的特征值代表最具有区分性的特征，且只有该特征会被激活。这种假设主要有两个缺点：首先，关于最大特征值代表最具区分性细节的先验知识可能并不总是正确的；其次，滑动窗口中的最大算子阻碍了基于梯度的优化，因为在反向传播中，梯度仅分配给局部最大值，如Saeedan 等［18］所述，这些稀疏的梯度将进一步加强这种不一致性。从某种意义上说，除非当前的最大值被抑制，否则一些有区分性的特征将永远不会成为最大值。

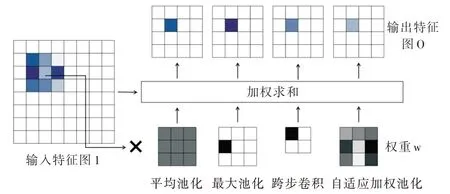
Fig.2 Different downsampling methods in the view of weighted summation图2 加权求和角度下的不同池化方式

2.2 跨步卷积

跨步卷积可以看作是步长为1的密集卷积，后接下采样［20］。在局部权重归一化函数中，这种下采样方式可表示为：

式中，I为经过步长为1的密集卷积后的特征图；s 既表示步长又表示滑动窗口的长宽。从这个角度来看，跨步卷积的下采样部分无法自适应地模拟下采样过程的重要性。此外，其仅关注每个滑动窗口内的一个固定位置，而将其余位置丢弃。该固定间隔采样方案将限制移位不变性，因为需要卷积后的特征出现在特定且非连续的位置才能激活。从这个意义上讲，微小的偏移和畸变会导致下采样后的特征发生巨大变化，从而干扰CNN的偏移不变性［20］。对于滑动窗口大小为1×1的跨步卷积，缺点会更加明显，因为特征图没有得到充分利用［21］，并且会引起棋盘效应［22］。

2.3 DPP 和基于信息熵理论的Weighted pooling

最近提出的DPP 使用细节标准作为重要性函数F，其通过滑动窗口中特征与激活统计数据的偏差对重要性进行衡量。DPP 通过设计更复杂的重要性函数并确保连续性以实现更好的梯度优化，进而解决最大池化存在的问题。然而，DPP 中的假设是启发式的，更详细的特征可能并不代表更具有区分性，例如杂乱的背景拥有的特征比前景中的纯色物体更详细。因此，DPP 可能会保留对任务不太有区分性的细节。在DPP 中手工制作的重要函数会将先验知识融入到下采样过程中，可能会导致区分任务的最终目标不一致。而基于信息熵理论的Weighted pooling 认为特征图中特征值出现的次数越多，该特征值就越重要，对应的重要性函数F 就越大。这种池化方式偏重于选择图像中出现次数多的特征，但并不一定是最具有区分性的特征。

通过以上分析可以得出理想池化层的要求。首先，下采样过程应尽可能处理较小的偏移和失真，因此应避免采用固定间隔采样方案，如跨步卷积使用的F 函数；其次，重要性函数F 应对判别特征具有选择性，而不是根据先验知识（如DPP 中使用的F 函数）手动设计。这种区分性措施应适应不同的任务，并由最终目标自动确定。

3 自适应加权池化

3.1 算法流程

为满足通过加权求和分析后提出的理想池化要求，本文提出自适应加权池化。通过赋予滑动窗口中每个特征值一个可变的权重参数，使网络通过反向传播最小化损失函数，进而自行选择权重参数大小。以大小为2×2的池化窗口为例，设4 个特征值分别为a1、a2、a3、a4，首先按照大小顺序对特征值进行排序，得到a(1)≥a(2)≥a(3)≥a(4)；然后根据特征值的大小顺序为每个特征值分配重要性参数k1、k2、k3、k4，这4 个参数的初始值为通过高斯分布生成的随机数；最后为使得到的权重参数非负且易于优化，在随机生成的重要性参数上增加exp(·)操作，即：

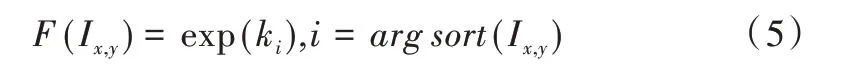
式中，arg sort(Ix,y)表示特征值Ix,y在滑动窗口中排序后的索引值。

由上述操作得到的权重大小等于将重要性参数进行Softmax 归一化后的值，因此可将自适应加权池化整理为以下步骤：

（1）输入：待池化的特征图，池化窗口大小n，神经网络损失函数J，神经网络训练学习率α。

（2）步骤1：根据每个池化层的池化窗口大小选择重要性参数个数，对于有n 个特征值ai(i=1,2,…,n)的池化窗口随机初始化n 个重要性参数ki(i=1,2,…,n)。

（3）步骤2：将每个池化窗口中的特征值从大到小进行排序得到a(1)≥a(2)≥…≥a(n)。

（4）步骤3：将初始化的重要性参数进行Softmax 归一化得到权重参数，表示为：

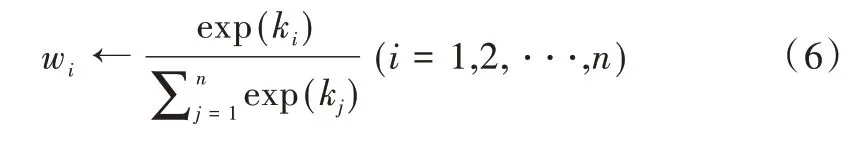
（5）步骤4：将权重参数与每个池化窗口中对应的特征值相乘后累加得到池化结果，表示为：

（6）步骤5：初始化的权重参数wi(i=1,2,…,n)在网络训练的过程中会随着反向传播的进行通过梯度下降不断迭代优化，直至收敛，表示为：

以上过程相当于网络自行选择了池化窗口中各个特征值所对应的重要性。自适应加权池化流程如图3 所示。

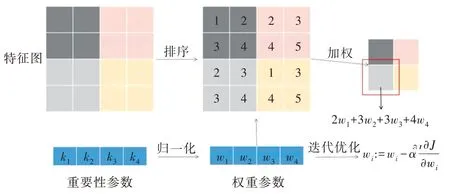
Fig.3 Adaptive weighted pooling process图3 自适应加权池化流程

3.2 权重参数的使用范围

常见的CNN 结构存在多个网络层，每层的特征图包含多个池化窗口，若在每个池化窗口中使用不同权重参数，那么需要训练的参数量十分庞大，网络难以训练且极度占用内存。若整个网络仅使用一组权重参数，相当于对所有类型的特征都采用同一种池化策略，不能满足实际需求，且无法处理网络中池化窗口大小可能不一致的情况。Hijazi 等［23］研究表明，不同卷积核提取不同的特征，例如高层卷积核提取高级特征。CNN 中的特征图在经过卷积后，同一个通道的特征值代表被一个卷积核提取出的同种类型特征，这表示在特征图的同一通道上仅使用一组权重参数不会扰乱池化过程对特征的提取。对于深层CNN 而言，每个通道使用一组权重参数仍会较大程度地增加网络中的训练参数量。为避免由于训练参数过多而导致过拟合现象发生，同时减少网络对内存的占用，每个池化层的特征值使用同一组权重参数，即在CNN的每个池化层上使用相同的池化策略。对于最常使用的2×2 池化窗口而言，每个池化层仅有4 个参数；对于池化窗口大小等于特征图尺寸的全局平均池化，其池化层参数量与特征图尺寸相同。

3.3 算法内存占用与复杂度分析

本文基于VGG16 网络［3］结构分析自适应加权池化对内存占用和计算量的影响。VGG16 中需要训练的参数有138M 个，每次迭代需要的浮点计算次数为15G 次，若将其中的最大池化全部使用2×2的自适应加权池化代替，则训练参数的增加量为20 个，整体增加比例约为千万分之一；计算次数增加20M 次，整体增加比例约为千分之一。由此可见，网络在使用自适应加权池化后，内存占用和计算量的增加都处于可接受的范围内。

4 实验方法与结果分析

4.1 数据集

本文所有实验均使用以下公开标准数据集：①Fashion-minist 数据集是一个时尚衣物的图像数据集，训练集包含60 000 张图片，测试集包含10 000 张图片，每张图片为28×28的灰度图，所有数据都有标签，共有10 类，分别为Tshirt/top、Trouser、Pullover、Dress、Coat、Sandal、Shirt、Sneaker、Bag、Ankle boot［24］；②Cifar10 数据集包含60 000 张图像，每张图像为32×32×3像素的彩色照片，训练集大小为50 000，测试集大小为10 000，照片分属10 个不同类别，分别为Airplane、Automobile、Bird、Cat、Deer、Dog、Frog、Horse、Ship、Truck［25］；③Omniglot 数据集包含50 个不同字母，共1 622类手写字符，每个类别有20 个样本，每个样本为28×28的灰度图。该数据集具有类别多、每类样本少的特点，常用于小样本图像分类任务中［26］。

4.2 网络结构使用

对于Fashion-minist 数据集分类，本文采用2 个卷积层、2 个下采样层、2 个全连接层的CNN 结构，具体结构信息如表1 所示，其中下采样层分别采用最大池化、平均池化、步长为2的3×3 卷积、自适应加权池化。该实验旨在比较4种不同下采样方式下的网络分类性能，并通过设定不同学习率以评价自适应加权池化的鲁棒性。

Table 1 Network structure for Fashion-minist classification表1 用于Fashion-minist 数据集分类的网络结构

对于Cifar10 数据集分类，本文使用两种不同的网络结构。第一种为2 层卷积层、2 层池化层、3 层全连接层的浅层CNN 结构，具体结构信息如表2 所示。考虑到对于自适应加权池化权重参数的初始化过于随机，可能会导致收敛至损失函数局部最小处，因此首先使用最大池化将网络迭代至收敛，保存网络参数，然后将池化方式改为自适应加权池化，权重参数的初始值设置为最大池化对应的权重参数值，此时自适应加权池化的初始状态等同于最大池化。载入最大池化模型的参数，对自适应加权池化模型进行fine-tune。比较fine-tune 前后测试集的准确率和损失，验证在较复杂的彩色图像数据集中，自适应加权池化相较于传统池化方式能否有更好的表现。

Table 2 Shallow CNN network structure for Cifar10 classification表2 用于Cifar10 分类的浅层CNN 网络结构

对Cifar10 数据集进行分类的第二种网络为ResNet18，具体结构如图4 所示。原始的ResNet18 网络在conv_block结构中使用了跨步卷积，在网络的最后使用了1 个全局平均池化层。本文将跨步卷积与由全局平均池化改成的自适应加权池化进行性能比较，观察池化方式更改前后的网络对测试集分类准确率和损失的影响。该实验旨在验证自适应加权池化不仅适用于浅层CNN，对深层CNN的性能也能有所提升。

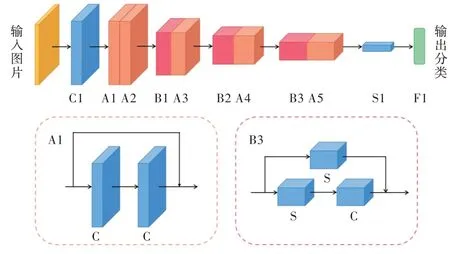
Fig.4 ResNet18 network structure图4 ResNet18 网络结构

对于Omniglot 数据集的小样本分类，本文采用Matching Network［27］的网络结构。该网络输入的每个batch 包含两个部分：一部分称为support set，包含20 个不同类别的图像；另一部分称为test example，含有1 个图像，该图像的类别与support set 中某个图像的类别相同。Matching Network包含两部分：第一部分用于提取输出图像特征，含有4 个卷积层和4 个池化层；第二部分用于类别划分，对提取出的test example 图像特征与support set 中每个图像的特征分别计算余弦距离，取20 个余弦距离中最大值对应的support set 图像类别作为test example的图像类别。Matching Network 网络结构如图5 所示。该实验旨在说明自适应加权池化不仅能提升数据量多的图像分类任务性能，也能提升小样本图像分类任务的性能。

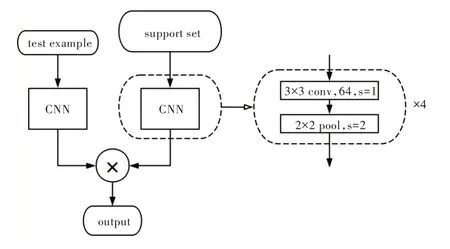
Fig.5 Matching network structure图5 Matching network 结构

4.3 实验结果分析

各种数据集与网络结构在不同池化方式下对应的测试集最优分类准确率和损失如表3 所示，以下详述。

使用CNN 网络对Fashion-minist 数据集进行分类，分别选取0.000 01～0.01 之间共7 种不同的学习率进行测试，在不同下采样方式下得到的测试集准确率随学习率的变化曲线如图6 所示。可以看到，自适应加权池化对准确率的提升较为明显。图6 中，网络的测试集分类准确率随着学习率的增长先增大后减小。最大池化、平均池化、跨步卷积、自适应加权池化作为下采样层的最高准确率分别为91.75%、92.09%、91.61%、92.30%。自适应加权池化相较于排名第2的平均池化，对分类准确率有0.21%的提升，且在学习率变化的情况下分类准确率一直处于较高水平，说明自适应加权池化具有较强的鲁棒性。

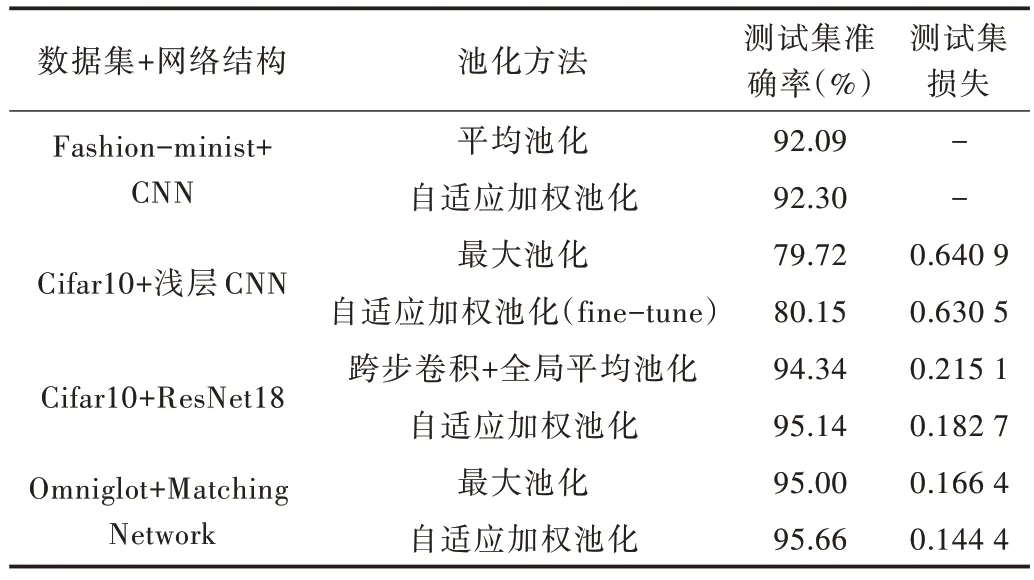
Table 3 Optimal classification accuracy and loss of the test set corresponding to various data sets and network structures under different pooling methods表3 各种数据集与网络结构在不同池化方式下对应的测试集最优分类准确率和损失

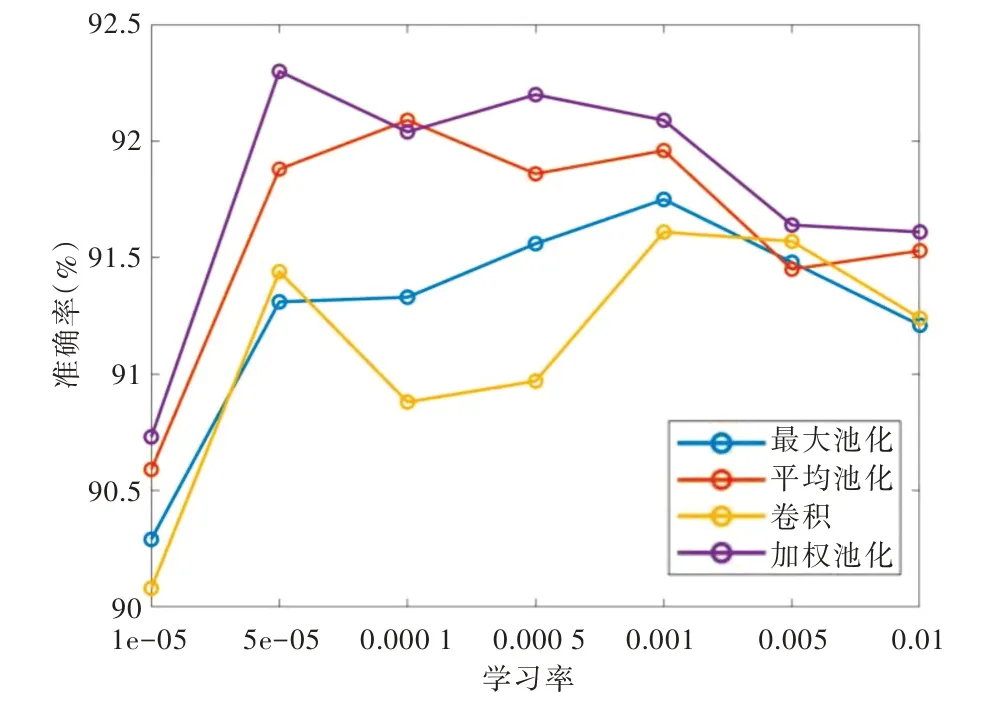
Fig.6 Classification accuracy of the Fashion-minist test set corresponding to each downsampling layer under different learning rates图6 不同学习率下各下采样层对应的Fashion-minist测试集分类准确率

在5 层CNN 网络结构下对Cifar10 数据集进行分类，首先设置池化层为最大池化，将网络迭代100 次，初始学习率设为0.001，迭代到40 次时将学习率降为0.000 1，迭代到80次时进一步降为0.000 01。100 次迭代完成后，保存此时网络中的训练参数，然后将池化层的池化方式更改为自适应加权池化，载入网络参数后进一步训练，此时设置网络继续迭代50 次，得到最终结果。经过自适应加权池化finetune 之后的网络测试准确率提高了约0.43%，测试损失降低约0.01，网络分类能力得到明显提升。

在ResNet18 网络结构下对Cifar10 数据集进行分类，设置网络迭代次数为200 次，初始学习率设为0.1，在迭代到100 次时将学习率降为0.01，在迭代到150 次时将学习率进一步降为0.001，网络分别使用原始ResNet18 和替换池化层后的ResNet18 进行训练。相较于跨步卷积和全局平均池化，使用自适应加权池化在Cifar10 测试集上的最优准确率提高了0.8%，最优损失降低了0.032。

使用Matching Network 结构对Omniglot 数据集进行小样本分类，选取前1 200 类为训练集，中间211 类为验证集，剩下211 类为测试集，batch 大小设置为32，每个训练epoch包含从训练集随机选取的1 000 个batch，每个测试epoch 包含随机从测试集选取的250 个batch，共迭代30 个epoch。相较于最大池化，使用自适应加权池化在Omniglot 测试集上的最优准确率提高了0.66%，最优损失降低了0.022。

5 结语

本文提出一种自适应加权池化方法，相较于常用池化方式，自适应加权池化能根据任务类型的不同，智能选取最优池化策略提取特征。实验结果表明，自适应加权池化能在少量增加内存占用和计算量的情况下提升网络性能，相较于传统池化方式，其在各种图像分类数据集和CNN 结构中均取得了更好的分类效果，在小样本分类任务中也得到了更优结果。自适应加权池化在不同学习率下均能保证较高的分类准确率，且具有良好的鲁棒性。自适应加权池化解决了传统池化方式不能客观评价池化窗口中每个特征值区分性大小的缺陷，保留了池化层本身的简洁性，并从实验上证明了分类问题的最优池化类型是介于最大池化和平均池化之间的某种池化方法，为提升CNN 网络性能提供了新思路。虽然理论上自适应加权池化只会少量增加网络的复杂度，但其相较于常用池化方法在深度学习框架上没有进行性能优化。后续研究将致力于提高自适应加权池化在各种深度学习框架上的使用性能。