信息解构整合 破解压轴难题——2018年安徽省中考数学压轴题的深度剖析

江苏省盱眙县第二中学 (邮编：211700)

问题(2018年安徽省中考数学试卷第23题)如图1，Rt△ABC中，∠ACB=90°，点D为边AC上一点，DE⊥AB于点E，点M为BD中点，CM的延长线交AB于点F.

(1)求证：CM=EM；

(2)若∠BAC=50°，求∠EMF的大小；

(3)如图2，若△DAE≌△CEM，点N为CM的中点，求证：AN∥EM.

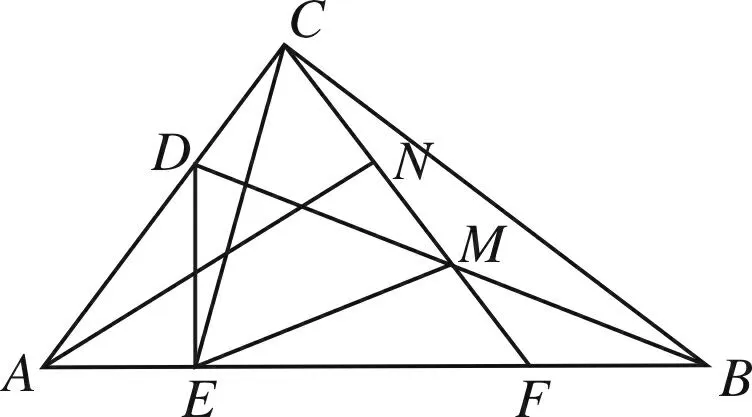
图1 图2

此道问题的图形是一个具有确定性的背景图形，特别是第(3)问，解法多样，涉及的知识面广.初中阶段主要的数学知识点如：三角形勾股定理、全等、相似、平行线的判定、解直角三角形等都可以在此题中加以应用，非常好地考查学生的几何直观、空间观念、运算能力、模型思想、推理能力等具有初中学段特色的数学核心素养，本文将重点从逻辑推理素养的角度解析此题并提供多种解法.

同样面对中考压轴题繁多的条件，学生处理方式不同，效果也会大不相同，原因为何？除去天赋因素，最大的差别在于其思维方式和思维习惯的不同.对于数学教学，如何培养科学的思维方式和良好的思维习惯是一个重要的课题.

数学解题中有两种思维：一种学生是根据问题的外部特征在记忆中搜索相同或相似的现成模式，依靠直觉采取切合的动作，若无相关信息就会一筹莫展不知所措；另一种学生是分析问题中的内在的数学结构，据此应用基本知识和方法解决问题，若不成功则反复在条件结论之间进行推理寻求联结.当然实际情况中这两种思维也是互相交织的，只是所占比例不同.

一种学生是“看”出解题思路和方法，另一种学生是“推”出解题思路和方法.

显然，对于新颖陌生的或隐蔽性强的或比较复杂的问题，只依靠“看”是解决不了的.必须引导学生根据题中的信息进行“推”，顺推是“进”，逆推是“退”，进退有序，寻找条件与结论的联结点，才是解决问题的好方式.

若将题中的条件看成“因”，将结论视为“果”，则本文主要研究第(3)问，先根据题目信息进行逻辑分析、解构重组：

进行了这样的信息解构整合之后，就可以在条件与结论之间进行寻求多种联结方式，自然会产生多种解题思路和方法.

策略一利用平行线判定方法

这是解决此题的主要思路，下面主要选取平行线的判定方法中的“同位角相等，两直线平行”进行研究；就此题而言，由于不止一对“同位角”，都可以进行尝试：

(1)若选择∠NAF与∠MEF作为同位角，因为∠MEF=30°，所以只要证得∠NAF=30°即可，可分直接证法与间接证法，先看直接证法：

图3

方法1 (解直角三角形)

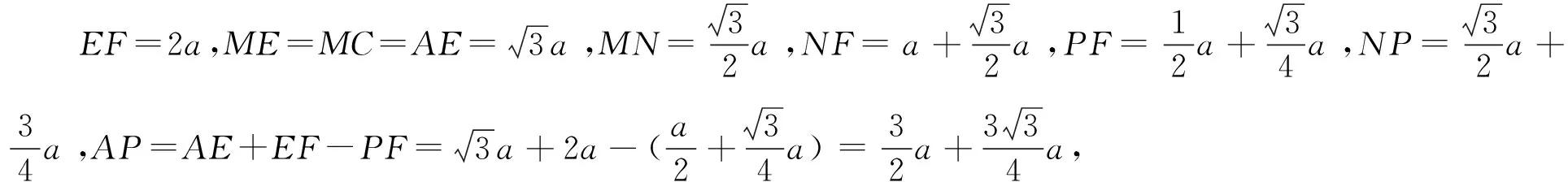
再看间接证法：

方法2 (相似法)

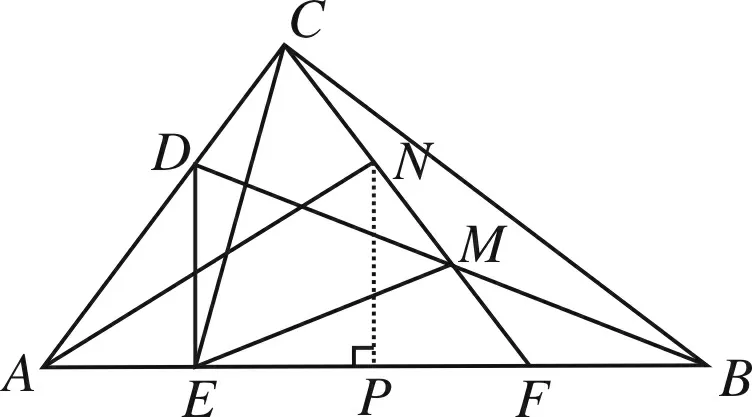
图4

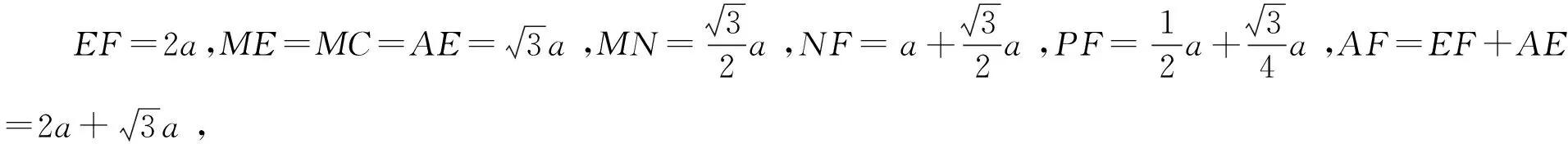
此法也可证△APN∽△NPF.

求证某一个角等于30°，解直角三角形法与相似推导法都是基本方法，优点是思路明确，缺点是计算量略大.

(2)若选择∠ANC与∠EMC作为同位角，因为∠EMC=∠AED=90°，所以只要证得∠ANC=90°即可，可分间接证法与直接证法，间接证法就是证明AN⊥CM，而点N为CM中点，由等腰三角形“三线合一”可得只要证得“AM=AC”即可，下面围绕证明“AM=AC”这一思路提供以下方法：

证“AM=AC”可采用“代数法”与“几何法”，代数法即利用勾股定理等方法将AM与AC用含相同参数的表达式表示出来，几何法：(1)若两条线段不在同一三角形中，常通过证明全等得出结论；(2)若两条线段在同一三角形中，可以通过“等角对等边”加以说明.

先看代数法两例：

方法3 (代数法①)

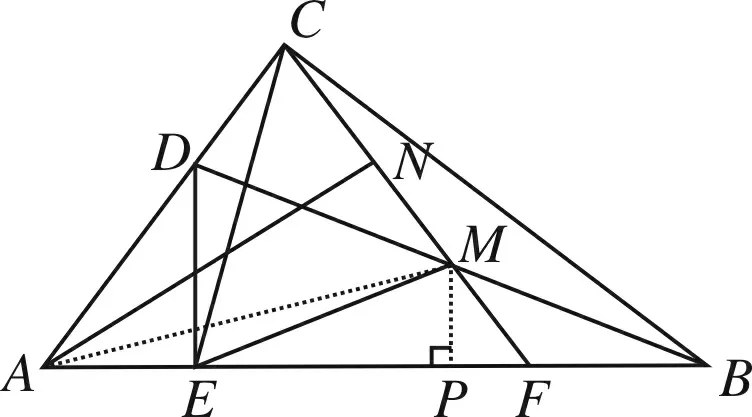
图5

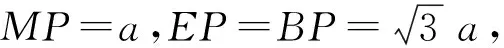
方法4 (代数法②)

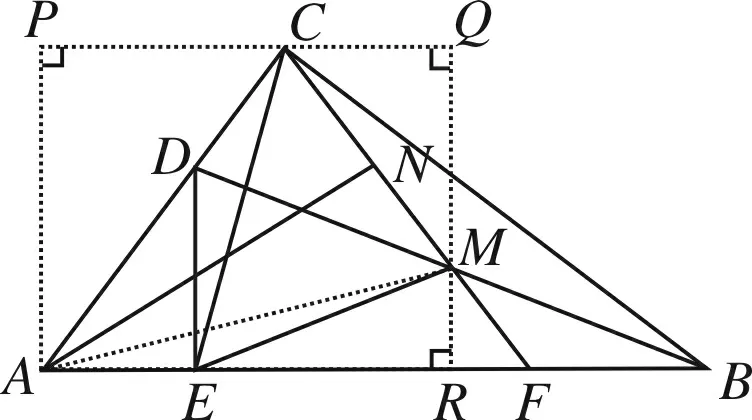
图6

三角形全等是证明线段相等的最常规办法，可以利用原图或采取构造的方式寻找全等三角形，下面列举几例：

方法5 (全等法①)

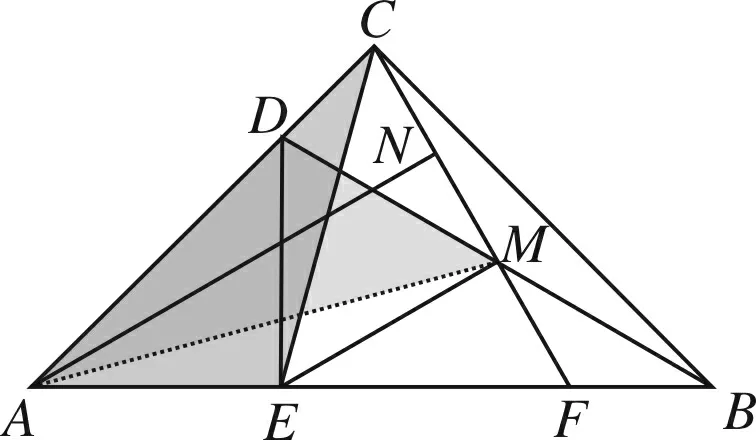
图7

简析在△ACE与△MAD中，因AE=MD，∠AEC=∠MDA=105°，CE=AD，则△ACE≌△MAD(SAS)，故AC=AM.

方法6 (全等法②)

图8

简析在△AEM与△CMB中，因AE=CM=EM=MB，∠AEM=∠CMB=150°，则△AEM≌△CMB(SAS)，故AC=AM.

还有以下几种巧妙构图方式，读者可以自行尝试：

方法7 (全等法③)

方法8 (全等法④)

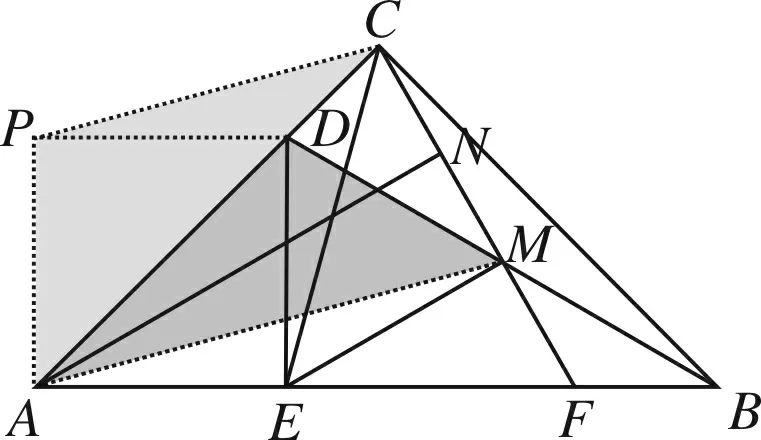
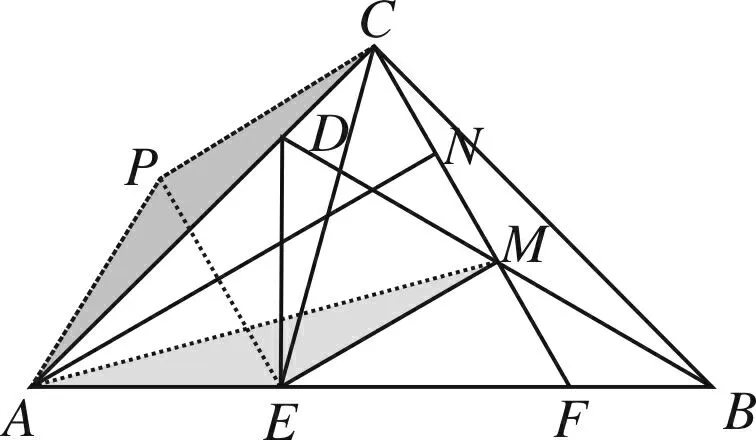
图9 图10

方法9 (直角三角形斜边中线等于斜边一半)

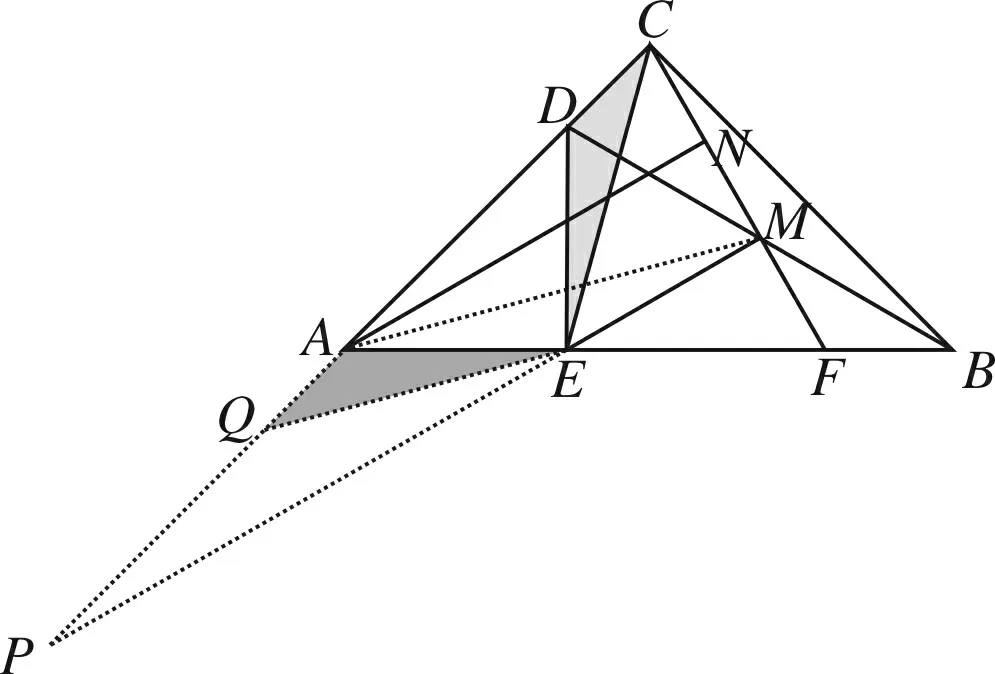
图11

下面介绍“∠ANC=90°”的直接证法：

方法10 (相似法)

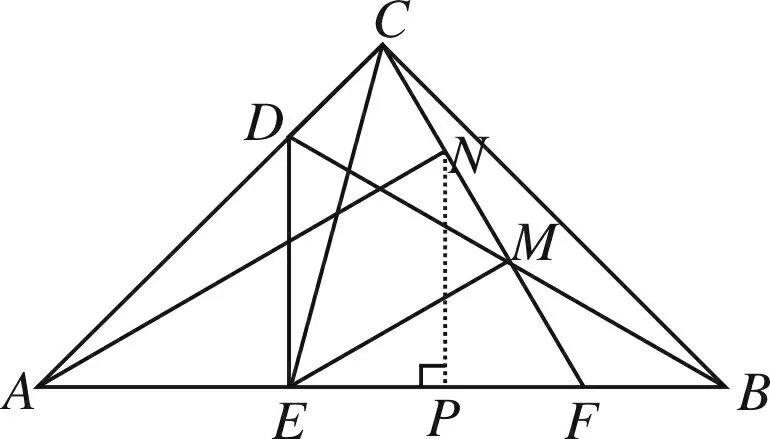
图12

简析证△AFN∽△NFP(过程同方法2，此处省略)，所以∠ANF=∠NPF=90°.

如果你觉得以上方法不够简便的话，让我们一起来见识下面这种巧妙构图：

方法11 (一线三等角全等法)

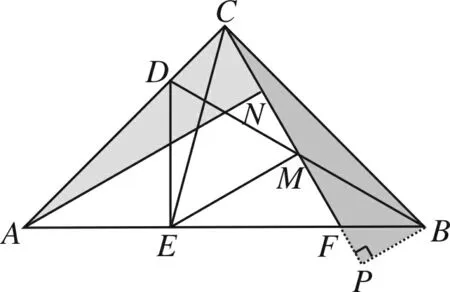
图13

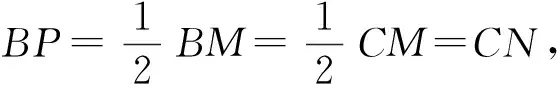
此法甚是精妙，当然这需要学生对几何模型有一定的构建功底，不难发现，它就是我们常见的异侧型一线三直角模型.

连接AM后，线段AM、AC位于同一三角形中，“等角对等边”这一方法自然会蹦出脑海，我们何必舍近求远？请看：

方法12 (等角对等边)

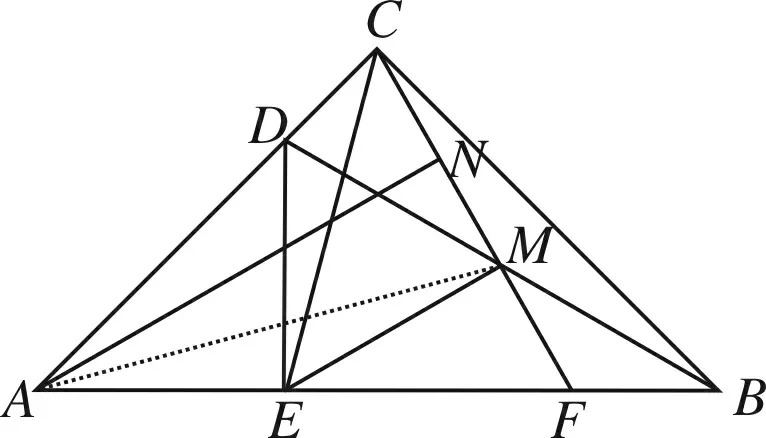
图14

简析如图，因∠ACM=∠ACE+∠ECM=30°+45°=75°，∠AMC=∠CME-∠AME=90°-15°=75°,则∠ACM=∠AMC,AM=AC.

若能将题目中的条件充分挖掘，此法的思路自然是清晰明了、水到渠成.

策略二平行于同一条直线的两条直线平行

因为平行于同一条直线的两条直线平行，因此，此题可以构造AN、EM之外的“第三方直线”，通过平行的传递性予以解决.

方法13

图15

简析过点C作CP∥ME交BA延长线于点P，则∠CPE=∠MEF=30°,在△ECP与△DAB中，因∠CPE=∠ABD=30°，∠CEP=∠ADB=105°，CE=AD，所以△ECP≌△DAB，PE=BD=2AE，即点A为PE中点，所以AN为梯形MCPE的中位线，AN∥CP∥ME.

此法也可采用倍长EA再证全等或构造母子型相似解决.

策略三构造A字型相似

方法14

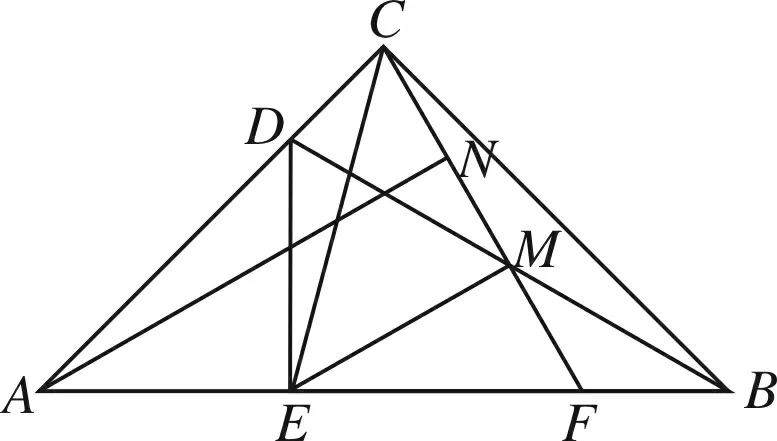
图16

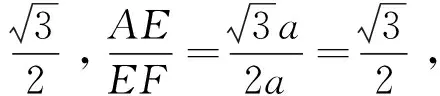
策略四构造含对边平行的特殊图形

在初中阶段，我们学习了多种含对边平行特征的图形，如平行四边形、矩形、菱形、正方形、梯形等，特别是平行四边形类图形只要证得其中一组对边平行，另外一组对边也就平行，此题用这种思路解决甚为巧妙.

方法15 (构造平行四边形)

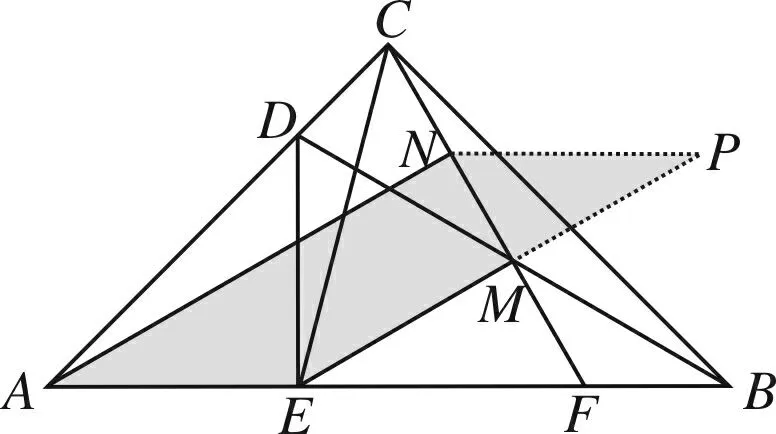
图17

简析过点N作AB的平行线交EM的延长线于点P，所以∠P=∠MEB=30°,PN=2MN=CM=AE,因PN∥AE,PN=AE,则四边形AEPN是平行四边形，即AN∥EM.

方法16 (构造矩形)

图18

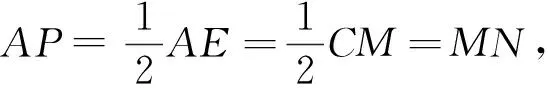
解题时依靠直觉根据记忆“看”出解题思路不可取，须得根据题目信息进行逻辑分析解构重组，做到进退有序，寻找条件与结论的联结点，从而轻松解决问题.