混合分数布朗运动环境下欧式障碍期权定价*
刘文倩,韦才敏,卜祥智
(1. 汕头大学 理学院, 广东 汕头 515063; 2. 汕头大学 商学院, 广东 汕头 515063)
1 引 言
期权是指持有人在确定时间,按确定价格向出售方购(销)一定数量和质量的原生资产的协议,但他不承担必须购入(销售)的义务.期权作为一种金融衍生产品,其定价取决于原生资产价格的变化.由于原生资产是一种风险资产,价格变化是随机的,因此期权的价格变化亦必是随机的.但是一旦原生资产价格确定下来,期权的价格亦将随之确定[1].1900年, Bachelier 首次利用随机游动的思想给出了股票价格运行的随机模型,并提到了期权定价,被公认是现代金融学的里程碑.1964年,Samuelson 对 Bachelier 的模型进行了修正,以股票的回报代替原模型中的股票价格,形成几何布朗运动模型[1].1973年Black和Scholesv[2]建立了看涨期权定价公式,其成果获得了诺贝尔经济学奖.
20世纪80年代初期起,资本市场的大量实证研究表明,金融资产(如股票)的对数收益率具有“尖峰厚尾”的特征,且价格变化也并非随机游走,而是呈现长期相关性和自相似性.分数布朗运动( Fractional Brownian Motion)具有加法不变性、自相似性、厚尾性以及长期相关性,因此成为刻画金融资产价格过程的重要工具[3].1989年Peters[4]用分数布朗运动来刻画将资产价格的变化规律. Duncan等[5]建立了一个关于分数布朗运动的基于Wick乘积的随机积分,称为分形It积分,在该积分下,Necula[6]给出了任意时刻分数布朗运动环境下的欧式期权定价公式.Elliott和Hoek[7]研究了Hurst指数在情况下的分数布朗运动,通过Wick积分的方法得到了Girsanov定理和分数It公式.Hu和Øksendal[8]通过Wick积分和分数白噪声分析进一步发展了分数布朗运动积分理论,并证明了It型分数Black-Scholes市场无套利且完备的.Bender[9]将其推广到任意Hurset指数.随后分数布朗运动下欧式期权定价模型[10]、欧式幂期权定价模型[11]和欧式障碍期权定价模型[12]分别被研究.
然而,Björk和Hult[13]研究表明基于Wick积分的分数布朗运动在金融中的应用会受到限制,而定义一个合适的关于分数布朗运动的随机积分也是比较困难的.且分数布朗运动不是一个半鞅(鞅,Martingale).为避免这些问题,并考虑金融资产价格过程的长记忆特性,可以使用混合分数布朗运动(Mixed Fractional Brownian Motion)来刻画金融资产的波动[14].Cheridito[15]首次在经济学中使用混合分数布朗运动.最近,Sun[16]研究了混合分数布朗环境中欧式汇率期权的定价问题.另外有学者分别研究了混合分数布朗运动下的欧式期权定价[17]和亚式期权定价[18].但是运用混合分数布朗运动模型研究期权定价问题的文献还较少,特别是在国内还未有关于混合分数布朗运动环境下障碍期权定价的研究.
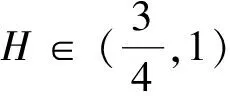
2 预备知识
定义1障碍期权是这样一张欧式期权合约,它的最终收益除了依赖于原生资产在期权到期日的价格,还与原生资产价格在整个期权有效期内是否达到某一规定水平(障碍)有关.当原生资产价格达到障碍时期权终止有效,这类期权称为敲出期权.若原生资产初始价格高于障碍,称为下降敲出期权;若原生资产初始价格低于障碍,则称为上升敲出期权.当原生资产价格达到障碍时期权开始有效,这类期权称为敲入期权.类似地,有下降敲入期权和上升敲入期权.[1]
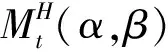
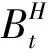
混合分数布朗运动满足如下性质:
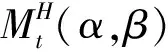
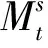
|S|2H-|t-S|2H);
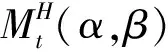
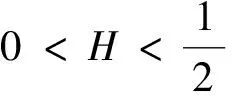
3 混合分数布朗运动下障碍期权定价公式
考虑金融市场上存在两种可自由、连续交易的资产, 无风险资产Mt(现金市场) 和风险资产St(股票). 标的资产需要支付红利, 到期日为时间T, 敲定价格为K, 障碍为B, 并作以下假设:
(ⅰ) 假设标的资产 (股票) 价格St满足混合分数布朗运动:

(ⅱ) 无风险资产(现金市场)价格Mt满足:
dMt=rtMtdt.
其中,r是常数,表示无风险利率;
(ⅲ) 原生资产连续支付股息 (红利), 红利率q;
(ⅳ) 市场不存在套利机会;
(ⅴ) 交易是连续的, 且允许买空卖空;
(ⅵ) 不支付交易费和税收.
引理1(混合分数 It公式)设Vt=V(St,t),V是一个关于St和t的二元可微函数. 若随机过程St适合随机微分方程:
(1)
则
(2)
证明由 Taylor 展式:
(3)
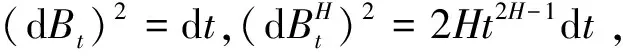
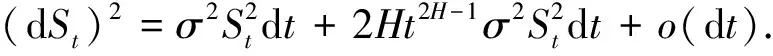
(4)
把式 (4) 代入到式 (3), 得
证毕.
令V=V(St,t) 表示欧式障碍期权在时刻t的价格. 形成投资组合 Π=V-ΔS(Δ是原生资产的份额), 应用混合分数 It公式, 在 [t,t+dt] 时间段内, 由假设(4), Π是无风险的,利用Δ-对冲有
dΠt=dVt-ΔtdSt-qΔtStdt=
qΔtStdt=r(Vt-ΔtSt)dt.
(5)

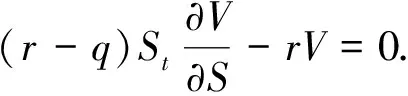
(6)
在定解区域内, 所有欧式障碍期权价格均满足该偏微分方程.
定理1若金融市场满足上述假设, 欧式下降敲出看涨期权(European down-and-out call option)敲定价格为K,障碍为B,在t∈[0,T]时刻的价格Cd.o为:
Cd.o(S,t)=Se-q(T-t)N(d1)-Ke-r(T-t)N(d2)-
Ke-r(T-t)N(d4)]=Cvanilla(S,t)-
(7)
其中
d1=
d3=
这里Cvanilla(S,t) 是欧式标准期权 ( vanilla options )在t∈[0,T] 时刻的价格.
证明由式(6)知,欧式下降敲出看涨障碍期权的数学模型为:在区域D={B 经如下变换: (ⅱ)令ω=ueβ(t),η=x+α(t),τ=ρ(t), 则 令 即有 则方程转化为热传导方程, 在{η∈R+,0≤t≤T}上适合定解问题: 上述 Cauchy 问题可表示为 Possion 公式: 则 代入 Poisson 公式有 由变换(ⅰ)和(ⅱ)回到原变量 (S,t) 以及函数Cd.o(S,t) ,立得定理结论. 证毕. 推论1若金融市场满足上述假设,欧式下降敲入看涨期权(European down-and-in call option)的定价公式 证明由于欧式期权是一个线性问题, 因此, 欧式障碍期权定价与标准欧式期权定价之间存在 Vvanilla(S,t)=Vd.o(S,t)+Vd.i(S,t)=Vu.o(S,t)+Vu.i(S,t). (8) 由式 (7) 和 式(8) 可推得结论. 证毕. 同理可以推得欧式上升敲出看涨期权和欧式上升敲入看涨期权的定价公式. 为了得到欧式看跌障碍期权定价的表达式, 建立如下关于看涨-看跌障碍期权的平价公式. 定理2若金融市场满足上述假设,下降敲出期权存在看涨-看跌平价公式: 其中 证明令W是下降敲出看涨期权与看跌期权之差: W=Cd.o(S,t)-Pd.o(S,t). 易知W(S,t) 在区域D={B 类似定理 1 的证明, 可得定理结论. 证毕. 本文采用混合分数布朗运动刻画股票价格的变化过程,以欧式下降敲出看涨期权为例,通过求解偏微分方程得到其定价公式的显示解.根据敲入与敲出障碍期权的关系以及看涨-看跌平价关系可依次推出欧式障碍期权所有类型的定价公式,改进了前人的分数布朗运动期权定价模型.但是,本文中的模型依然在Black-Scholes理论框架下,且为简化模型所作的假设与现实情况有一定出入,所以模型有待进一步改进和修正,如何使模型更贴近现实金融市场有待更多的深入研究.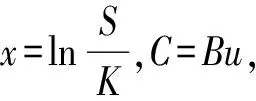
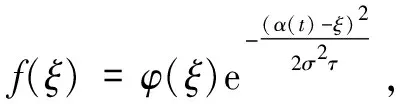
4 结 论

