两比例失效率元件组成串联系统元件冗余与系统冗余的随机比较*

张建东，颜荣芳

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

1 引 言

随着经济全球化的迅猛发展, 经济产业精细化程度越来越高, 物流运输、银行支付、电商服务等大型复杂系统的矛盾日益凸显, 其中如何提高和改善大型复杂系统的可靠性成了经济发展过程中亟待解决的重要问题. 例如, 全球生产商(华为, 微软等)努力提高产品供应链系统的可靠性, 第三方支付公司(阿里, Paypal等)竭力保障系统的可靠性与安全稳定性. 因此, 在经济高速发展的时代研究大型复杂系统的可靠性与安全性变得尤为重要.

在各种各样的大型复杂系统中, 每一个元件的寿命越大, 整个系统的寿命也越大, 将这样的系统称为协同系统(Barlow and Proschan(1975)[1]). 根据元件的连接方式, 又将协同系统分为n中取k系统、并联系统、串联系统.为了有效地研究复杂系统的可靠性, 借助最小路集的理论, 可将协同系统等价为多个串联系统的并联; 同时, 通过最小割集的方法, 将协同系统等效为多个并联系统的串联. 因此, 为了研究并联系统与串联系统的可靠性问题, 首先需要建立复杂系统的可靠性理论. Barlow and Proschan(1975)在普通随机序下给出了串联系统中元件冗余优于系统冗余的结论(BP原理). Boland等(1992)[2]分别考虑了由两个寿命独立异分布元件组成的串联系统和并联系统的热冗余元件和冷冗余元件的分配问题, 就如何分配冗余元件给出了一些充分条件, 并得到了冗余系统寿命比较的普通随机序. 基于Boland等(1992)的研究, Singh等(1994)[3]在所有元件寿命服从指数分布的条件下, 讨论了串联系统的热冗余分配问题, 给出了冗余系统寿命比较的失效率序, 同时还考虑了由两个元件组成的并联系统的冷单冗余分配问题, 得到了冗余系统寿命比较的随机占优序. Valdés等(2006)[4]考虑了两个独立异分布的初始元件组成的串联系统中的热冗余分配问题, 分析了元件失效率对分配策略的影响, 给出了冗余系统寿命比较的失效率序. 鉴于Singh等(1994)的研究, Li等(2008)[5]讨论了两个元件组成串联系统的热单冗余分配, 建立了冗余系统寿命比较的增凸序与随机占优序, 而对于两个元件组成并联系统的冷单冗余分配, 得到了冗余系统寿命比较的随机占优序. Brito等(2011)[6]给出了冗余系统寿命比较的反失效率序, 进一步丰富和完善了Valdés等(2006)的结果. Li等[7]在随机占优序下比较了两个温备元件的分配问题. Zhao等(2012)[8]进一步将Singh等(1994)的结论从失效率序推广到似然比序, 同时还讨论了由两个元件组成的并联系统的冷单冗余分配问题, 给出了冗余系统寿命比较的似然比序. Nanda等(2013)[9]在一般的协同系统中将BP原理推广到了反失效率序以及似然比序. Hazra and Nanda (2014)[10]在一般的协同系统中将BP原理推广到了失效率序. Zhao等(2015)[11]对于温备情形, 在串联系统中给出了BP原理的似然比序, 在并联系统中给出了BP原理的普通随机序；对于热备情形, 在串联系统中也给出了BP原理的似然比序. Zhao等(2017)[12]研究了由n个元件组成的串联系统的冗余分配问题, 将Zhao等(2012)的结论从两个元件的情形推广到n个元件的情形. Yan等(2016)[13]研究了由n个寿命独立异分布的初始元件组成串联系统的热单冗余分配问题, 在反失效率序意义下给出了冗余的分配策略, 将Valdés等(2006)的结果从两个初始元件推广至多个初始元件的情形, 同时将Brito等(2011)的结论从匹配情形推广到不匹配情形. 在匹配情形下, 大多数的文献都是基于元件寿命服从特定分布(例如指数分布, Gamma分布和Weibull分布等)的假设进行研究, 在各种随机序下对冗余分配策略作出随机比较. 然而在现实生产活动中, 元件的寿命往往是未知的, 使特定分布下得到的冗余分配方案不再具有一般性. 因此, 在元件服从一般寿命分布的条件下, 如何有效地改善与提高系统的可靠性与稳定性成为了可靠性理论与可靠性工程中面临的重大问题. 有关冗余分配理论更多的讨论可参阅You and Li(2014)[14], Da and Ding(2016)[15]和Fang and Li(2018)[16]等文献.

不同于以上文献, 这里主要研究了两个比例失效率元件组成的串联系统, 在元件寿命相互独立的条件下, 对于元件冗余与系统冗余两种分配方式, 分别在普通随机序、失效率序、反失效率序下作出了讨论, 得到了元件冗余是最优分配策略的结论.

2 模型假设及符号说明

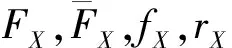
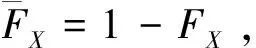
(ⅲ)若对于任意的x∈R,FY/FX关于x是递增的,则称X反失效率序下小于Y.记作X≤rhY.

众所周知, 失效率序与反失效率序都蕴含了普通随机序, 然而失效率序与反失效率序之间并没有必然的联系, 由普通随机序既不能得失效率序也不能得失效率序.有关随机序详细的讨论可以参阅Shaked and Shanthikumar(2007)[17]和Müller and Stoyan (2002)[18].

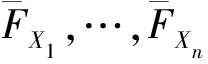
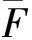
为了提高系统的可靠性, 经常给系统元件附加冗余元件, 根据元件附加方式的不同, 可以将冗余分配方式分为元件冗余(见图1)与系统冗余(见图2), 所谓元件冗余是指给系统中的每一个初始元件附加一个冗余元件, 系统冗余是指给原始系统并联一个冗余元件组成的系统. 其中元件冗余又可分为热备份和冷备份,热备份是指初始元件与冗余元件寿命的最大值, 而冷备份是指初始元件与冗余元件寿命的卷积.本文将考虑两比例失效率元件元件组成的串联系统, 对元件冗余方式与系统冗余两种分配策略作出随机比较, 得到最优的分配方案.

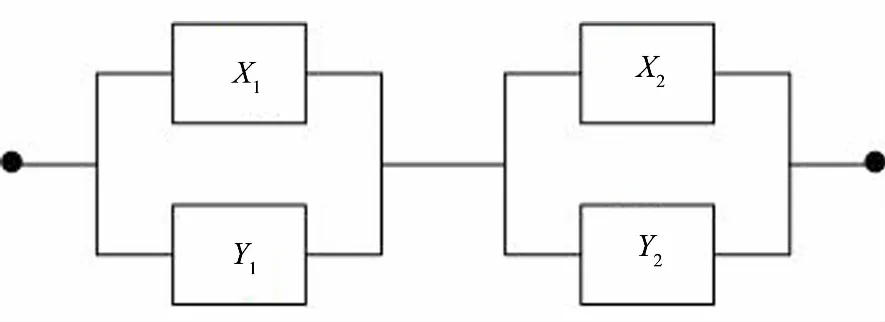
图1 元件冗余

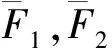
τ(X∨Y)=(X1∨Y1)∧(X2∨Y2)表示图1中的元件冗余的寿命，τ(X)∨τ(Y)=(X1∧X2)∨(Y1∧Y2)表示图2中的系统冗余的寿命.

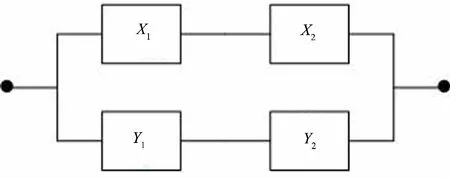
图2 系统冗余

3 元件冗余与系统冗余的随机比较

定理1假设X1,X2是两个独立的随机变量分别具有比例参数λ1,λ2,Y1,Y2是另外两个独立的随机变量分别也具有比例参数λ1,λ2, 那么

τ(X∨Y)=(X1∨Y1)∧(X2∨Y2)≥st

τ(X)∨τ(Y)=(X1∧X2)∨(Y1∧Y2)．

证明使用元件冗余方案时, 串联系统的可靠性函数为

采用系统冗余策略时, 串联系统的可靠性函数表达为

将两种方案的可靠性函数作差, 即

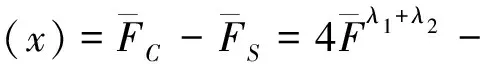
至此, 定理1得证.

定理2设X1,X2是两个独立的随机变量分别具有比例参数λ1,λ2,Y1,Y2是另外两个独立的随机变量分别也具有比例参数λ1,λ2, 那么

τ(X∨Y)=(X1∨Y1)∧(X2∨Y2)≥hr

τ(X)∨τ(Y)=(X1∧X2)∨(Y1∧Y2)．

证明为了建立元件冗余与系统冗余的失效率序, 将元件冗余与系统冗余方案的可靠性函数作比值, 即

因此，

所以y2(x)关于x是递增的, 故完成了定理2的证明.

定理3设X1,X2是两个独立的随机变量分别具有比例参数λ1,λ2,Y1,Y2是另外两个独立的随机变量分别具有比例参数λ1,λ2, 那么

τ(X∨Y)=(X1∨Y1)∧(X2∨Y2)≥rh

τ(X)∨τ(Y)=(X1∧X2)∨(Y1∧Y2)．

证明为了得到元件冗余与系统冗余的失效率序, 将元件冗余与系统冗余方案的分布函数作比值, 即

进一步有

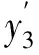
不失一般性, 假设0<λ1≤λ2, 从而有

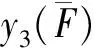
4 结 论

对于两组比例失效率元件组成的串联系统, 将元件冗余与系统冗余两种方式在普通随机序、失效率序、反失效率序下做出了随机比较, 得到了最优的冗余方案, 元件冗余优于系统冗余, 即

τ(X∨Y)=(X1∨Y1)∧(X2∨Y2)≥st

(X1∧X2)∨(Y1∧Y2)=τ(X)∨τ(Y);

τ(X∨Y)=(X1∨Y1)∧(X2∨Y2)≥hr

(X1∧X2)∨(Y1∧Y2)=τ(X)∨τ(Y);

τ(X∨Y)=(X1∨Y1)∧(X2∨Y2)≥rh

(X1∧X2)∨(Y1∧Y2)=τ(X)∨τ(Y).

这里只讨论了热备冗余情形下, 两组比例失效率元件组成的串联系统元件冗余与系统冗余的最优分配问题.对于串联系统、串联系统、协同系统的温备情形, 或者相依元件组成系统的冗余分配问题, 为确定冗余系统的分布函数带来了极大地困难, 一些关键的理论问题依然悬而未决, 一些富有挑战性的应用问题亟待解决, 这将是以后的研究方向.