可再生能源系统的不确定性优化模型及求解*

阳彩霞

(华南理工大学广州学院 计算机工程学院，广东 广州 510800)

1 引 言

可再生能源具有资源分布广、开发潜力大、环境影响小、可永续利用的特点.科学合理地制定可再生能源规划有利于推动节能减排进程、提高电源结构低碳化程度、促进智能化绿色电力的发展，对落实国家可再生能源规划、实施可再生能源重点发展领域、项目实施优先布局及制定相关政策具有重要的理论与应用价值.过去不少学者研究了可再生能源规划模型. Motaz Amer等(2013)[1]建立了混合可再生能源系统的优化模型，并利用粒子群优化技术降低系统成本；吉平等(2013)[2]对目前国内外应用于能源规划研究的集成结构模型及其现状进行了综述，重点总结了一些混合能源模型的结构及应用现状，并指出了当前存在的一些问题和未来的发展方向；宋杰鲲等(2013)[3]构建了山东省能源-经济-环境系统模糊机会约束目标规划模型，应用混合智能算法进行求解；Masoud Sharafia等(2014)[4]建立了成本和二氧化碳排放量最低、系统可靠性最高的多目标混合可再生能源系统优化模型，并用粒子群优化仿真方法求解；Kuo-Hao Chang等(2015)[5]新提出一种基于反应面的仿真优化技术，结合蒙特卡罗仿真方法，在不确定环境下实现混合可再生能源系统的模糊优化设计；万中等(2009)[6]给出了不确定环境下地市级可再生能源管理问题的确定性等价模型，但没有分析解的稳定性.

为了能从不同部门、不同时期、不同目标的角度反映不同能源活动与社会经济、环境之间的复杂关系，以及由系统条件动态变化所带来的不确定性，结合基于新随机变量序关系的满意度方法、区间线性规划和混合整数规划，研究了在多态不确定环境下具备多种能源形式统一协调规划功能的能源规划模型，并用算例分析了不同满意度水平下解的稳定性.结果表明该模型能综合考虑经济、环境、技术等方面因素，统一实现能源、经济、供应、转化、需求、社会、环境等功能，为政府分析制定相关能源、经济、环境政策提供参考意见.

2 基于新随机变量序关系的满意度法

注：x和y不能同时为常数，否则上述定义没有意义.

下面讨论随机不等式的确定性等价类求法.

设有不等式

AX≤b．

(1)

其中，A=(α1,α2,…,αn)，X=(x1,x2,…,xn)T，b∈R. 若A，b均是随机变量，决策者对式(1)的满意度水平为λ0，则

(2)

式(2)即为随机不等式(1)的确定性等价类.

新提出的满意度法与机会约束法的确定性等价类结构相似，只是非线性部分参数的意义不同，一个表示决策者的满意度水平，另一个是分布函数在某一置信水平下的反函数值. 但满意度法无需考虑随机参数的分布类型，只需知道其期望和方差，使用起来更简便.

3 城市群可再生能源系统规划模型

考虑三个地区在三个规划期内的一个能源动态规划方案.假设每个地区都有传统能源(柴油、汽油、天然气、煤炭等)、可再生能源(水力、太阳能、风力等)和多个终端消费部门(分为工业、农业、商业/民用和交通四个部门)及相关技术(可再生能源和化石燃料两种发电技术)；精炼石油产品(柴、汽油)主要用于交通，部分用于储备应急发电；天然气用于工、商业需求；煤炭除满足工商业需求外，还用于火力发电；可再生能源主要用于发电；电力供工、商、农业三部门使用(见图1所示).每种发电设备都有容量限制，但在三个规划期内能增容一次.若终端消费部门的能源需求量在容量限制范围内，则只存在固定成本；若需求量超过容量限制，则产生额外的增容成本.

图1 能源结构与终端消费部门之间的关系

可再生能源的可利用量容易随时间空间的变化而变化.有些还具有概率分布特征，如太阳能可利用量服从正态分布，风力可利用量服从韦伯分布[7].而水力可利用量、能源价格、需求量、发电转化率等不确定参数的精确概率分布信息较难获得，却容易得到其大致取值范围，因此可用区间数[a-,a+]表示.目标函数为最小化能源供应成本、发电固定成本和增容成本3部分的和，约束条件分为能源供需平衡、可再生能源的可利用量、电力平衡、发电厂装机容量(包括可再生能源、柴汽油)和决策变量等五类限制，建立该方案下的可再生能源管理系统优化模型. 用提出的基于随机变量序关系的满意度方法处理其中的随机参数，结合区间线性规划[8]和混合整数规划，可得到下列两阶段的等价子模型.

1)最好最优解子模型

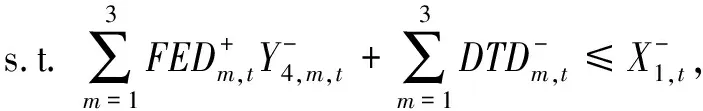
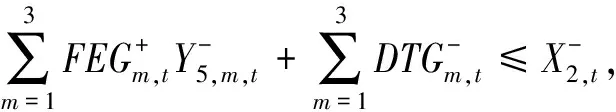
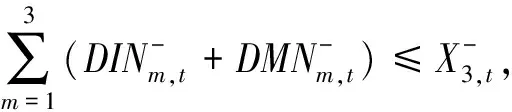
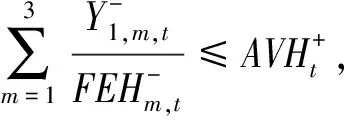
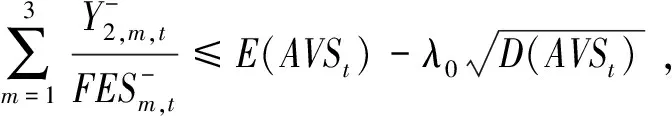
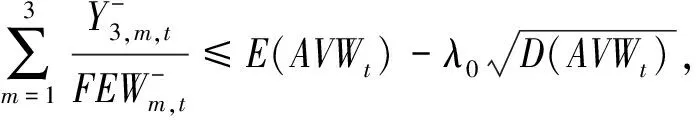
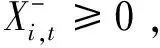
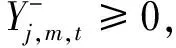
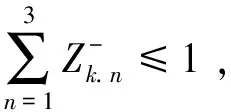
2)最差最优解子模型

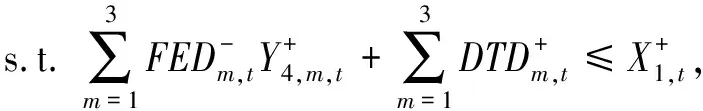
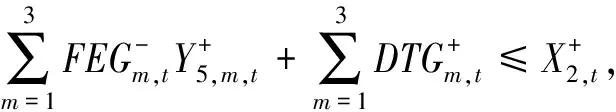
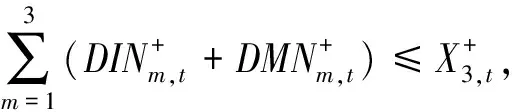
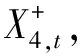
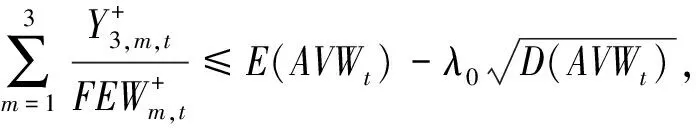
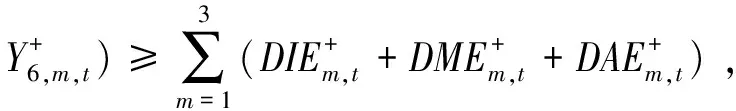
RCH+UCAP，

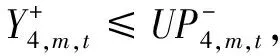
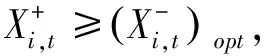
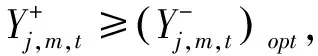
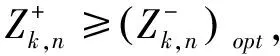
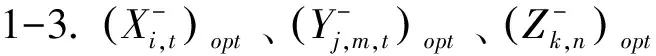
上述模型不仅能反映各种能源、各种发电技术、各个部门之间的竞争关系，还能处理以区间数、随机变量及其结合形式出现的不确定性，并且考虑了动态增容问题，可用来分析在不同经济和社会水平影响下与能源有关的政策方案.

4 实例求解与结果分析

假设3个地区的发电技术水平一样，故发电成本和转化率一样；储备的发电柴、汽油量上限一样.在3个规划期内的能源供应成本、发电成本及各种技术指标数值见表1. 3种可再生能源的残余装机容量分别为RCH=[500，2000]，RCS=[450，540]，RCW=[640，700](MW)，转化系数UCAP=60%. 假设可再生能源的发电设备均有三种增容选择(见表2). 三个地区在各个规划期内的各种能源总需求量见表3. 在不同满意度水平λ0下，得到模型的区间最优解和最优值(见表4，未列出的决策变量取值均为0).

表1 不同时期的成本、转化率等参数

表2 可再生能源发电增容 MW

1)由表4可知，系统最优值f和大部分最优解均是区间数，如λ0=0.1,X21=[55.27,58.27]表示第一规划期内汽油的供应量最好值为55.27 TJ，最差值为58.27 TJ；又如λ0=1时，Y313=[9.18,10.06]表示第一个地区在第3个规划期内的风力发电量最好值为9.18 MW，最差值为10.06 MW；而少数最优解为确定数，如λ0=1时，Y223=3.9表示第二个地区在第3个规划期内的太阳能发电量为3.9 MW.

2)随机不等式的满意度水平越高，代表约束条件的违反度越低，系统总成本势必越高.这说明要保障能源安全性和系统可靠性，须付出更多的成本代价.

3)由于满意度水平影响的是含太阳能和风能可利用量的随机不等式，所以在不同满意度水平下，常规能源的供应量Xi,t未变，只有3种可再生能源的发电量发生了变化，而柴、汽油和煤炭由于发电成本相对较高，发电转化率相对较低，故发电量为0，即无需柴、汽油和煤炭发电.

4)由于可再生能源发电设备的增容成本太高，在现有容量能满足各规划期内的电量需求情形下，增容变量均为0，即选择不增容.

5)目标函数中的参数PDt，PGt，PNt和PCt的大小及区间长度不影响系统的最优解，但影响系统的最优值.

6)约束条件中的参数至关重要，如各部门对各种能源的需要量过大，或各能源的可利用量过小，均会导致系统无解.

7)由于第三规划期内太阳能和风力的发电成本降低较多，而发电转化率又大幅提高，故三个地区均在第三规划期内选择太阳能和风力发电. 而水力的发电成本和转换率相对其他能源优势明显，在三个规划期内变化不大，故不同地区在不同规划期内均有所涉及.

综上所述，数值实验结果表明所建模型能给出不同系统违反水平下的能源配置方式及增容计划，可为当地政府提供决策参考.