基于惠更斯—菲涅耳原理激光传输特性的空间相干性分析

赵承良 卢兴园 李成金

(苏州大学物理科学与技术学院,江苏 苏州 215006)

光波的空间相干性和时间相干性问题是大学物理教学过程中的教学难点,不仅需要教师具有一定的激光方面的专业知识,而且也难以找到一种较为直观的方法让学生能够理解并接受．本文选取高斯谢尔模光束作为部分相干光的理论模型,通过获得高斯谢尔模光束通过杨氏双缝后的解析表达式,调控入射光束的相干宽度来直观地分析激光束的相干性对干涉条纹的变化情况,不仅可以加深学生对光波空间相干性和时间相干性的认识,也可以直观的分析入射部分相干光的相干宽度、缝间距和缝宽对干涉条纹的影响,并学会运用反称度的方法来判断相干宽度的大小．

1 高斯谢尔模光束通过杨氏双缝的传输分析

从某种意义上讲,自然界存在的所有光源都是部分相干的,理想的相干光和完全非相干光都不存在．首先光源的频率不可能是完全单频,其次光源在传播过程中都存在不稳定因素,从而直接影响空间和时间相干性．即使对于单色性很高的激光,严格意义上讲也是部分相干的．由于部分相干光的传输特性与严格的相干光的传输规律有本质区别,所以利用部分相干光理论来研究部分相干激光传输变换特性显得十分必要．[1]近年来,关于完全相干和部分相干光作为光源对通过杨氏双缝的干涉条纹进行了研究,[2-6]但是利用部分相干光模型,并且得到通过杨氏双缝之后的传输解析解并没有相关的研究报道．而部分相干光模型中最为常见及简单的理论模型为高斯谢尔模光束(Gaussian-Schell Model,缩写为GSM),由E.Collett和E.Wolf在1978 年提出的,[7]光束横向截面具有高斯型的光强分布和相干性分布,这种部分相干的光束在许多文献中被广泛研究．高斯谢尔模光束的矢量表达式为

W(r1,r2,0)=

(1)

其中,r1≡(x1,y1)和r2≡(x2,y2)为观察屏上的横向坐标位置矢量,σ0为束腰宽度,δ0为空间相干度．

在傍轴条件下,高斯谢尔模光束通过自由空间传输的表达式可以用下面的广义惠更斯菲尼尔公式获得[8]

(2)

其中,k=2π/λ为波数,λ为波长,u1≡(u1v1)和u2≡(u2v2)为观察屏上的横向坐标位置矢量．

图1是杨氏双缝干涉实验的装置示意图,b为缝宽,2a+b为缝间距,A面为高斯谢尔模光束的入射面,B面为出射光束的出射面,x1,y1,x2和y2为入射面上的坐标参数,u1,v1,u2和v2为出射面上的坐标参数．从双缝到观察屏的距离为z．双缝的传输公式可以用H(x,y)表示,其中a≤|x|≤a+b和-a-b≤|x|≤-a的情况下H(x,y)=1,反之则是0．因此对公式(2)进行适当的修改,高斯谢尔模光束通过双缝的传输可以用修改后的惠更斯菲尼尔积分公式表示:

图1 高斯谢尔模光束通过杨氏双缝传输的示意图

(3)

为了方便计算和分析,将双缝的传输函数展开成有限的高斯模型的和:

(4)

其中Am和Bm为高斯复数,可以直接利用最优算法获得,具体Am和Bm的值可以从文献[9]获得．一般来讲M越大精度越高,但是M=10的参数也足够的．[10,11]

将公式(1)和(4)代入公式(3),经过较为复杂的推导和积分,观察屏的交叉谱密度公式为

W(u1,u2,z)=

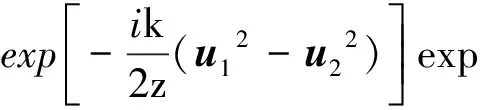
(5)

图2—图5显示的是高斯谢尔模光束通过杨氏双缝之后在观察屏处(z=700 mm),在不同入射相干宽度和缝宽的强度分布(等高线)．入射相干宽度越大代表该光束越接近于完全相干光,相干宽度越小则代表着越接近完全非相干光．从图中可以看出,在观察屏处的干涉条纹受到了入射光相干宽度的影响非常明显,当相干宽度较大时,还是能够看到较为清晰的干涉条纹,干涉条纹明暗相间清晰可见[见图2(a)、图3(a)、图4(a)和图5(a)],但是随着入射光的相干宽度逐渐减小,其相干条纹变的模糊,越来越变的不清晰可分辨,当相干宽度继续减小,已完全看不到明暗相间的干涉条纹,最后变成类高斯分布[见图2(f)、图3(f)、图4(f)和图5(f)]．

为了更好地对比缝宽的变化对激光束通过杨氏双缝干涉的影响,笔者对不同缝宽的干涉进行了研究．图2和图3的缝宽为b=0.2 mm,图4和图5的缝宽为b=0.1 mm,同时为了更直观和清晰地观察缝宽,笔者提供了v=0条件下的二维图．从图3和图5可以非常清晰地看出,在相同相干宽度条件下,缝宽越小,干涉条纹越清晰,明暗相间条纹越容易分辨,并且在相同入射光相干宽度条件下,缝宽越小抗相干宽度变化越强,但是等相干宽度继续减小时,最终都变成类高斯分布的结果．研究结果表明,光的空间相干性会影响光束的传输特性．

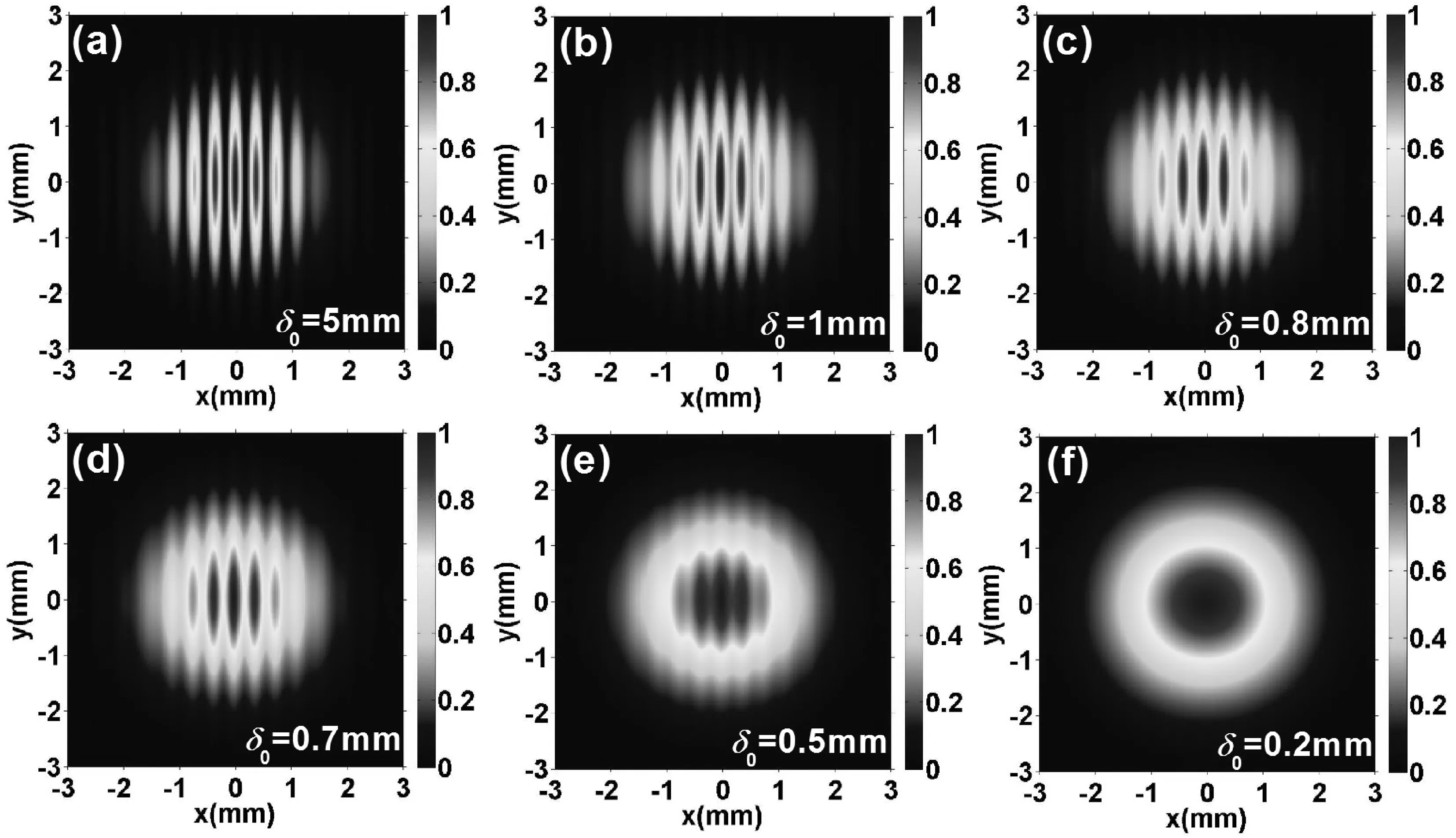
图2 高斯谢尔模光束通过杨氏双缝传输之后的归一化光强分布(等高线图),

图3 高斯谢尔模光束通过杨氏双缝传输之后的归一化光强分布(v=0),

图4 高斯谢尔模光束通过杨氏双缝传输之后的归一化光强分布(等高线图),

图5 高斯谢尔模光束通过杨氏双缝传输之后的归一化光强分布(v=0),

设一非单色光源发出的光传输到空间z处时,在任意空间两点r1,r2处的光场表示为E(x1,y1)和E(x2,y2),则该两时空点r1,r2之间光场的互相干函数定义为

W(x1,y1,x2,y2,z)=

[E(x1,y1,z)E*(x2,y2,z)],

(6)

式(6)的归一化形式为

μ(x1,y1,x2,y2,z)=

(7)

函数W(x1,y1,x2,y2,z)或μ(x1,y1,x2,y2,z)考虑了空间相关性．将μ(x1,y1,x2,y2,z)称之为相干度,如果μ(x1,y1,x2,y2,z)=1,则该光场是完全相干的．如果μ(x1,y1,x2,y2,z)=0,则该光场是完全非相干光．

为了更好的研究高斯谢尔模光束在观察屏上的相干度分布情况,根据式(5)和式(7),高斯谢尔模光束通过杨氏双缝传输之后在观察屏处的相干度表达式为

(8)

高斯谢尔模光束通过杨氏双缝之后在不同入射相干宽度和不同缝宽的相干度进行了研究(见图6和图7),从图中可得,在观察屏干涉条纹的相干度分布结构和入射高斯谢尔模光束的相干度分布结构不同,在u方向和v方向都呈现空间结构,从u方向可以看出,在不同入射光相干宽度和缝宽条件下,观察屏处的相干度分布具有类似光栅的结构,并且具有固定的周期．同时也可以得到随着缝宽的减小,在光谱处的相干度分布的周期变长．也意味着可以通过调节入射高斯谢尔模光束的相干宽度来调控观察屏的相干度结构,实现光场调控．

图6 高斯谢尔模光束通过杨氏双缝传输后在观察屏处

图7 高斯谢尔模光束通过杨氏双缝传输后在观察屏处

在普通物理学课程教学中,干涉条纹的反衬度γ是用于定义描述干涉现象明暗的显著程度,其定义为

(6)

公式(6)中Imax和Imin分别是干涉场中的光强极大值和极小值．当Imin=0时,即暗纹全黑,这时条纹的反差最大,干涉清晰可见,γ=1,意味着入射光束的接近于完全相干;当Imax→Imin,即明纹与暗纹的强度接近,条纹模糊不清,干涉不可分辨,γ≈0,意味着入射光束的相干性很低甚至接近于0,因此,γ的取值范围为0≤γ≤1．从上可知,入射光相干宽度的变化也直接影响着反称度的值的变化．图8显示的就是在不同缝宽条件下反衬度的值随着入射高斯谢尔模光束的相干宽度变化情况,从图中可以得出,当入射高斯谢尔模光束的相干宽度比较大时,入射光接近完全相干光,得到明暗完全清晰可见的干涉条纹,反称度则为1．当入射高斯谢尔模光束的相干宽度很小时,如图3(f)和图5(f)所示,则干涉条纹则完全不可见,因此反称度为0．

图8 高斯谢尔模光束通过杨氏双缝传输后在观察屏处

3 结论

本文针对大学物理教学过程中出现的关于光的相干性的知识难点,提出利用高斯谢尔模光束作为部分相干光的理论模型,研究由光束的相干性变化对双缝干涉条纹的变化．利用惠更斯—菲尼尔积分公式和对双缝小孔进行高斯展开的方式获得了高斯谢尔模光束通过杨氏双缝的解析表达式.该表达式的获得可以更好地研究光观察屏的光强分布、相干度分布．研究结果表明,随着入射部分相干光的相干宽度的减小,在观察屏处的干涉条纹明暗相间变的越来越难分辨,甚至完全不可分辨,并且在相同相干宽度条件下,缝宽越小其干涉条纹越容易分辨．观察屏处的相干度分布也进行了讨论,能够得到光栅周期性结构(u方向)的相干度分布,相干度的周期分布只与缝宽有关而与入射光的相干宽度无关．最后也将相干宽度与反称度的值进行了比较,得到了其两者一致的变化趋势．